- 세상의 모든 계산기 수학, 과학, 공학 이야기 공학 ()
[문제] 점성유체 - 전단력이 0이 되는 지점의 높이는?
문제:
바닥으로부터 높이 \( y \)(m)일 때 유속이 \( v(y) = -2y^2 + 4y\) (m/s)인 점성유체가 흐르고 있습니다.
이 유체의 전단력이 0이 되는 지점까지의 높이는 얼마입니까?
1. \( 1 \)
2. \( 2 \)
3. \( 3 \)
4. \( 4 \)
해설:
유속이 \( v(y) = -2y^2 + 4y \)로 주어졌을 때, 전단력은 유체의 점성에 의한 힘으로, 뉴턴의 점성 법칙에 의해 다음과 같이 주어집니다:
\[ \tau = \mu \frac{dv}{dy} \]
여기서 \( \mu \)는 유체의 점성계수입니다.
유속 분포에 따라 \( \frac{dv}{dy} \)를 구하면:
\[ \frac{dv}{dy} = \frac{d}{dy} \left( -2y^2 + 4y \right) = -4y + 4 \]
전단력이 0이 되는 지점을 찾기 위해 \( \tau = 0 \)이 되는 \( y \)값을 찾습니다:
\[ \tau = \mu \left( -4y + 4 \right) \]
\[ 0 = \mu \left( -4y + 4 \right) \]
점성계수 \( \mu \)가 0이 아니므로:
\[ -4y + 4 = 0 \]
\[ 4y = 4 \]
\[ y = 1 \]
따라서 전단력이 0이 되는 지점의 높이는 \( y = 1 \)입니다.
정답은 1번, \( 1 \)입니다.
점성유체 (Viscous fluid) :
점성유체는 흐름에 대한 내부 저항을 가진 유체를 말합니다. 이러한 유체는 움직일 때 마찰력이 발생하며, 이로 인해 에너지가 소산됩니다. 점성의 정도는 유체마다 다르며, 점성이 높을수록 유체의 흐름에 대한 저항이 커집니다.
주요 특징:
- 흐름에 대한 내부 저항 존재
- 층류 흐름에서 속도 구배 발생
- 점성으로 인한 에너지 손실
예시: 꿀, 오일, 물 등
전단력 (Shear force) :
전단력은 물체의 한 부분을 다른 부분에 대해 평행하게 미끄러지게 하는 힘입니다. 유체 역학에서 전단력은 유체 층 사이에 작용하는 힘으로, 점성유체의 흐름을 이해하는 데 중요한 개념입니다.
주요 특징:
- 물체나 유체의 표면에 평행하게 작용
- 유체의 변형률과 관련됨
- 점성유체의 흐름에서 중요한 역할
점성유체와 전단력은 밀접한 관련이 있습니다. 점성유체가 흐를 때, 유체 층 사이에 속도 차이가 발생하며, 이로 인해 전단력이 생깁니다. 이 전단력은 유체의 흐름을 방해하고 에너지를 소산시키는 역할을 합니다.
댓글2
-
세상의모든계산기
유속과 전단력을 그래프로 나타내려면,
먼저 주어진 유속 함수 \( v(y) = -2y^2 + 4y \)와 전단력 \( \tau = \mu \left( -4y + 4 \right) \)를 그래프로 표현하면 됩니다.
여기서 전단력은 점성계수 \( \mu \)에 비례합니다.
import numpy as np import matplotlib.pyplot as plt # Define the height range y = np.linspace(0, 4, 400) # Define the velocity function v = -2 * y**2 + 4 * y # Define the shear stress function (assuming mu = 1 for simplicity) mu = 1 tau = mu * (-4 * y + 4) # Plot the velocity profile plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.plot(y, v, label='Velocity (v)') plt.axhline(0, color='gray', linewidth=0.5, linestyle='--') plt.axvline(1, color='red', linewidth=0.5, linestyle='--', label='Shear stress = 0 at y=1') plt.title('Velocity Profile') plt.xlabel('Height (y)') plt.ylabel('Velocity (v)') plt.legend() plt.grid(True) # Plot the shear stress profile plt.subplot(1, 2, 2) plt.plot(y, tau, label='Shear Stress (τ)', color='orange') plt.axhline(0, color='gray', linewidth=0.5, linestyle='--') plt.axvline(1, color='red', linewidth=0.5, linestyle='--', label='Shear stress = 0 at y=1') plt.title('Shear Stress Profile') plt.xlabel('Height (y)') plt.ylabel('Shear Stress (τ)') plt.legend() plt.grid(True) plt.tight_layout() plt.show()위 코드는 다음과 같이 작동합니다:
1. \( y \)의 범위를 0에서 4까지 정의합니다.
2. 주어진 유속 함수 \( v(y) = -2y^2 + 4y \)를 계산합니다.
3. 전단력 함수 \( \tau = \mu (-4y + 4) \)를 계산합니다. 여기서 \( \mu = 1 \)로 가정합니다.
4. 두 개의 서브플롯을 만들어 유속 프로파일과 전단력 프로파일을 각각 그래프로 그립니다.위의 코드를 실행하면 유속과 전단력의 그래프가 나타납니다. 유속 그래프에서는 포물선 형태의 곡선을 볼 수 있으며, 전단력 그래프에서는 직선의 기울기가 -4인 그래프를 볼 수 있습니다.
이제 이 코드를 실행해 보겠습니다.
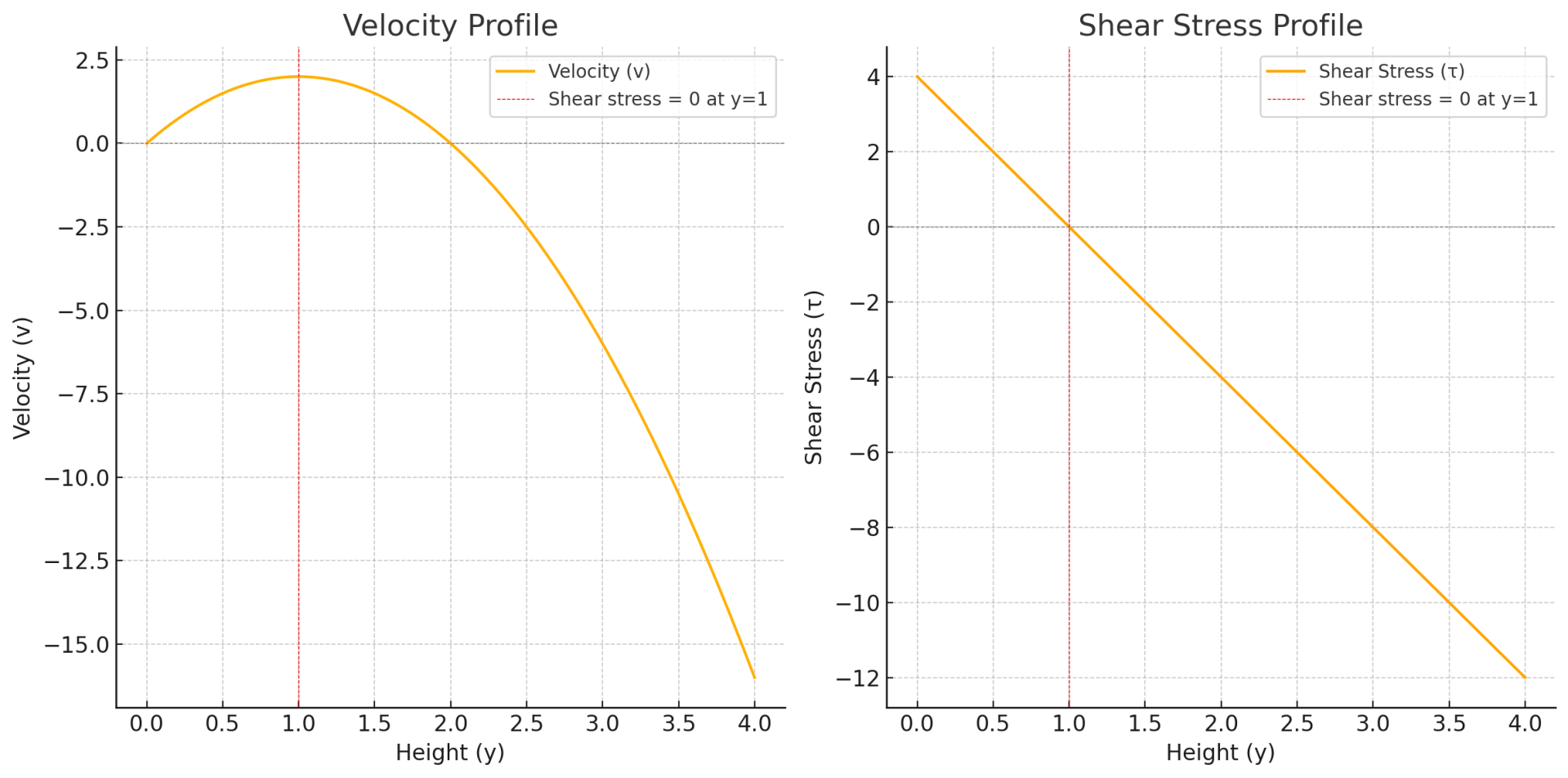
위 그래프는 주어진 조건에 따른 유속과 전단력을 나타낸 것입니다.
1. **유속 프로파일** (왼쪽 그래프):
- 유속 함수 \( v(y) = -2y^2 + 4y \)는 포물선 형태를 띠며, \( y = 1 \)에서 최대값을 가집니다.
- \( y = 0 \) 및 \( y = 2 \)에서 유속은 0이 됩니다.2. **전단력 프로파일** (오른쪽 그래프):
- 전단력 함수 \( \tau = \mu (-4y + 4) \)는 기울기가 -4인 직선입니다.
- \( y = 1 \)에서 전단력이 0이 됩니다.이 그래프를 통해 유속이 최대가 되는 지점과 전단력이 0이 되는 지점을 명확하게 확인할 수 있습니다.
-
세상의모든계산기
fx-570 ES 의 solve 로 구할 수 없는지?
fx-570 ES 와 같은 보급형 공학용 계산기에서는 solve 기능 내에서 미분(계수)처리를 할 수 없습니다.
따라서 solve 기능으로 답을 찾을 수는 없습니다.
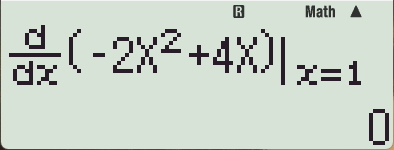

 로 템플릿 불러오고 수식과 x=1 부분 완성.
로 템플릿 불러오고 수식과 x=1 부분 완성.이런 식으로 x=1, x=2, x=3, x=4
모두 대입해 보고 0이 나오는지 확인하는 방법은 있습니다.
미분하는 것보다는 느리겠죠?


세상의모든계산기 님의 최근 댓글
991CW+ KR 버전이 나오면, 그 때는 (어쩔 수 없이) CW 를 추천하게 될지도 모르겠습니다. 2026 01.14 참고리뷰 : https://www.reddit.com/r/calculators/comments/1o7kj7f/casio_fx9910cw_review_a_much_needed_improvement/ 카시오 FX-9910CW 리뷰: 절실히 필요했던 개선이지만… 너무 늦은 감이 있는 걸까? 2026 01.13 기사 시험 용도 - EX든 CW든 뭘 쓰셔도 점수에는 영향이 없음. - 선택기준 1 : 과거에 fx-570ES Plus 을 써 봤다 -> EX 추천 - 선택기준 2 : 주변에 ES 또는 EX 계산기 사용법 알려줄 사람이 있다 -> EX 추천 // CW도 마찬가지 - 선택기준 3 : EX 정품을 높지 않은 가격으로 구하는데 문제가 없다? -> EX 추천 // EX 단종 이슈 + 짝퉁 이슈 있음. - 선택기준 4 : 모험을 좋아한다 -> CW 추천 참고 https://gall.dcinside.com/mgallery/board/view/?id=calc&no=312 2026 01.13 fx-9910CW 한국 출시관련 정보는 없습니다. 2026 01.13 기간을 넉넉하게 잡고 봐야 할 듯 싶구요. 기다려 본 결과... '실패함'이 떴습니다. 잘 된건지 잘 못된 건지 아무 변화가 없는건지... 뭐가 뭔지 모르겠네요. 2026 01.03