Tetration, Power Tower Function 을 이용한 프렉탈 패턴 찾기 #mytetration
-
- 2025.07.09 - 03:13 2024.05.25 - 18:33 3011 7
관련 프로젝트 링크
https://github.com/DMTPARK/mytetration
https://github.com/creeras/mytetration/tree/main/cuda
https://tetration.org/original/Tetration/index.html
1. 테트레이션 Tetration
거듭제곱을 거듭하여 만들어지는 연산
--> 0차? 연산, 다음수, a' = a+1
--> 1차 연산, 덧셈, a+n = a+1+1+1+1+......+1
--> 2차 연산, 곱셈=덧셈을 거듭, a*n = a+a+a+a+......+a
--> 3차 연산, 거듭제곱=곱셈을 거듭, = a*a*a*a*......*a
--> 4차 연산, 거듭제곱을 거듭, = a^a^a^a^...^a
(왼쪽에서 오른쪽 연산? 오른쪽에서 왼쪽 연산? right-to-left 라고 위키에 적혀 있네요.)
2. (Infinite) Power Tower Function, PTF
f(x) = x^x^x^x^x^x^...... 무한대의 함수입니다.
그걸 프로그램으로 적당히 계산시켜 볼 수 있습니다. (무한대면 계산에 끝이 없겠죠?)
특히 x가 복소수일때를 컴퓨터로 발산하는지 수렴하는지를 좌표평면상에 표시해 보면
아주 재밌는 모양(Fractal) 이 그려집니다.
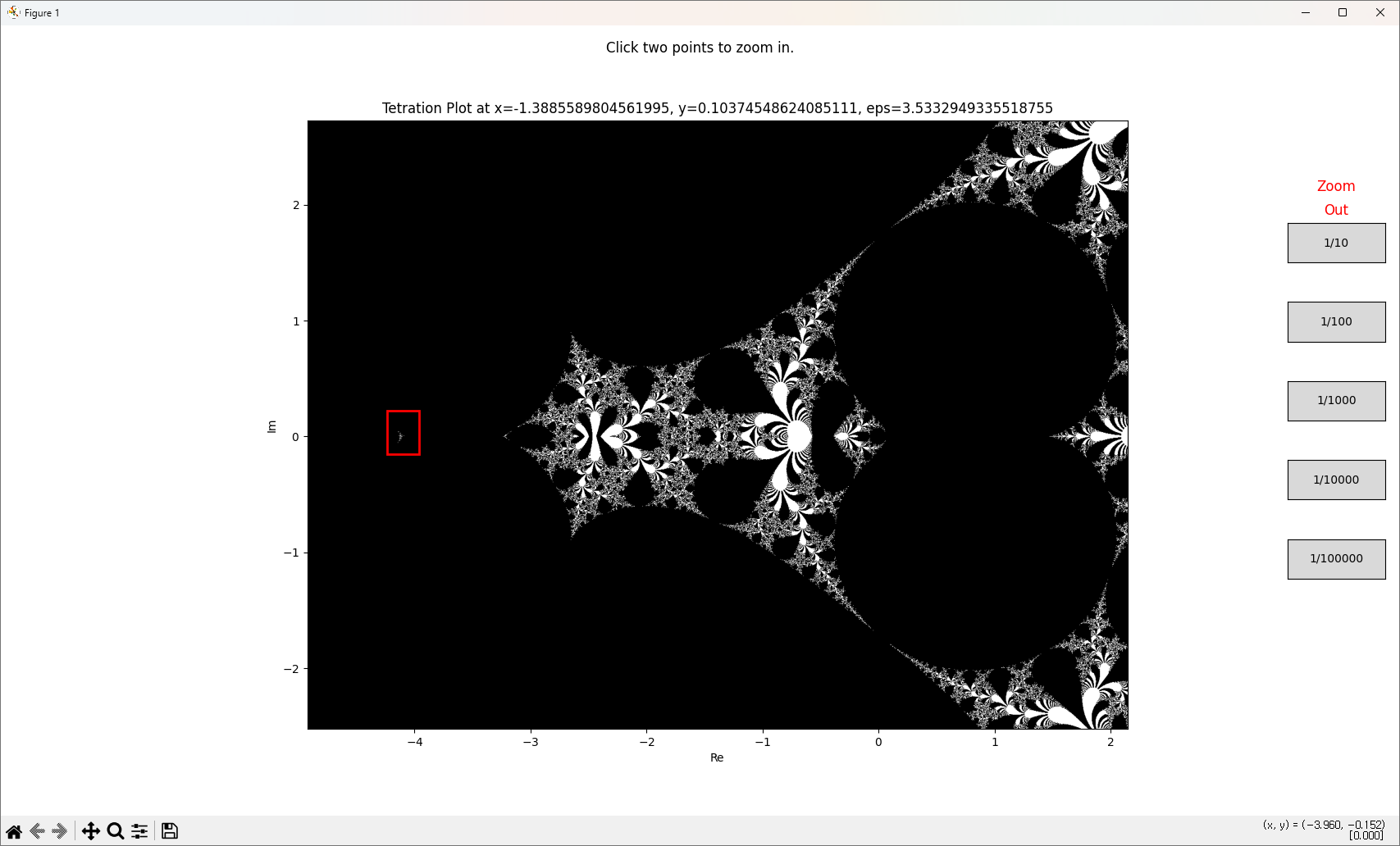
대충 이런 식인데, 일부분을 확대해 보면 신기한 패턴이 또 나오고
그 일부분을 또 확대해 보면
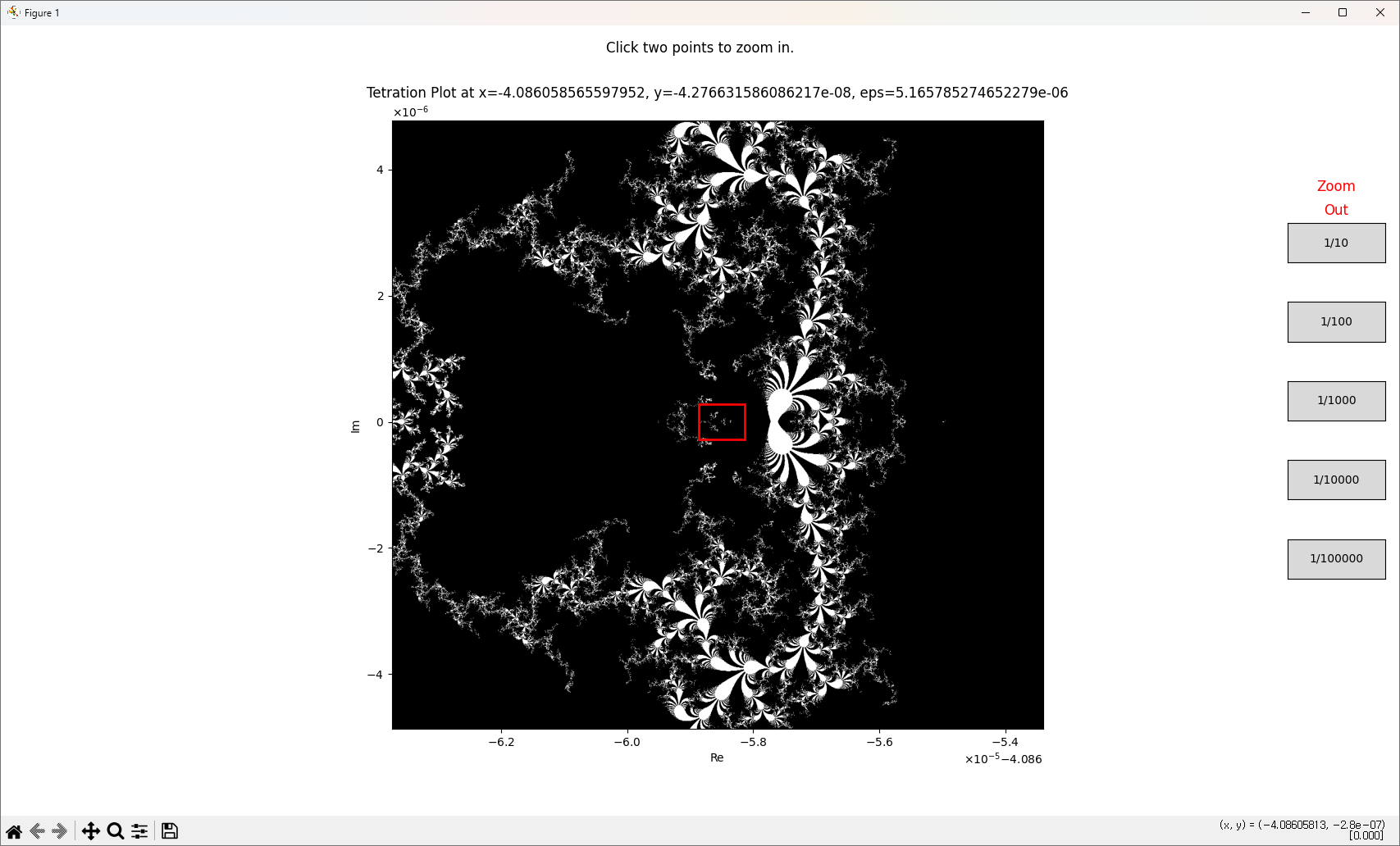
또 신기한 패턴이 또 나오고...
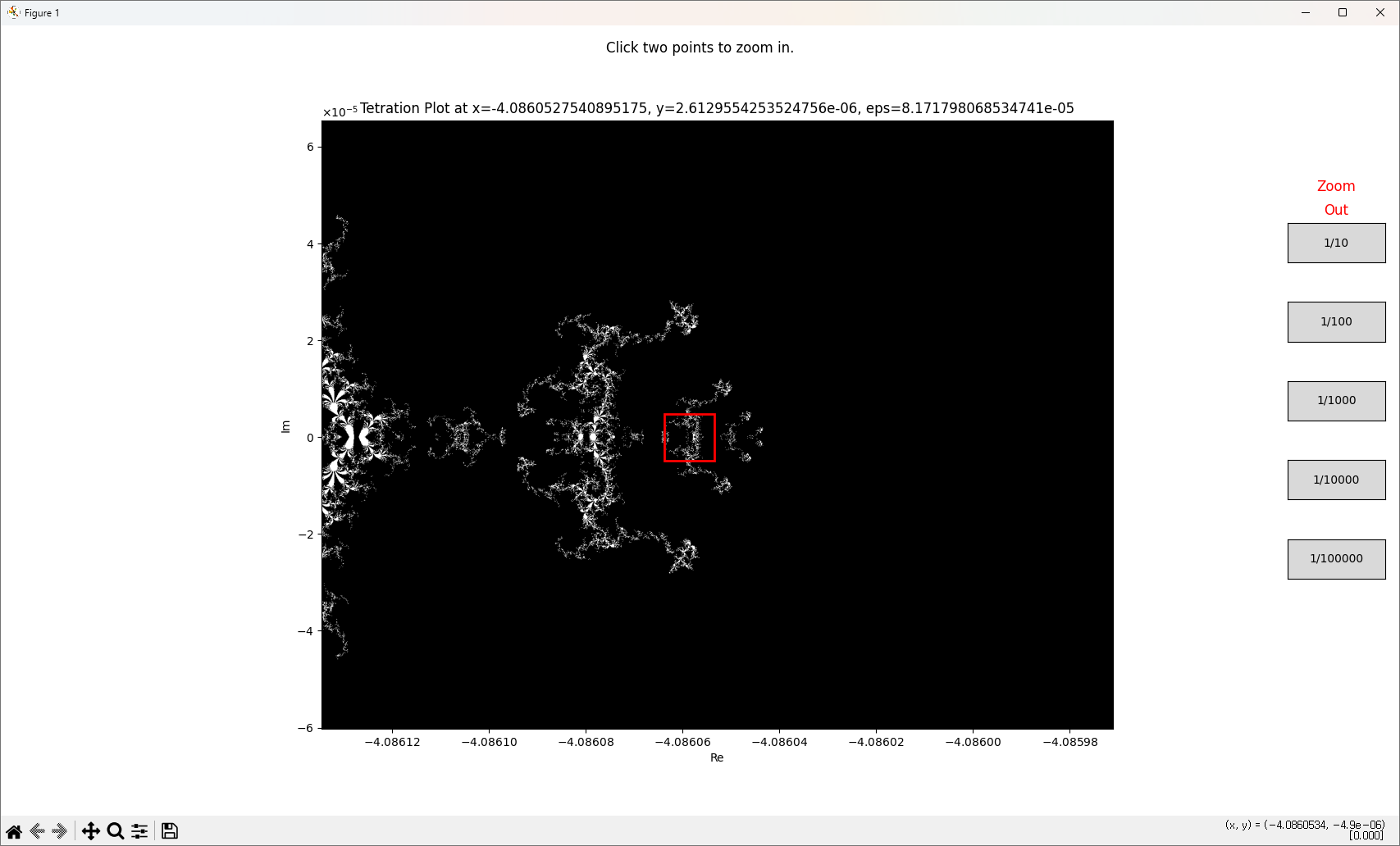
반복
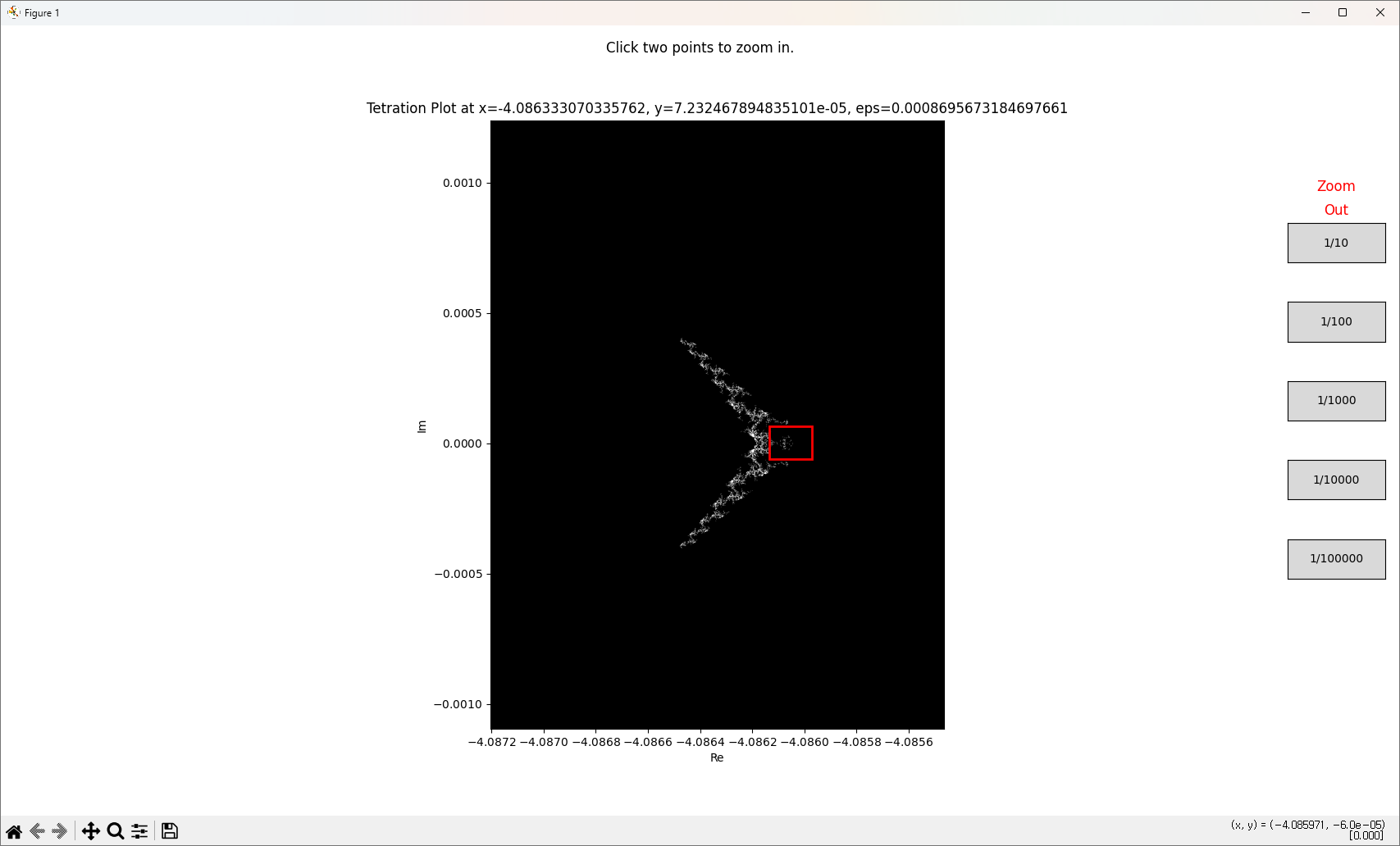
반복
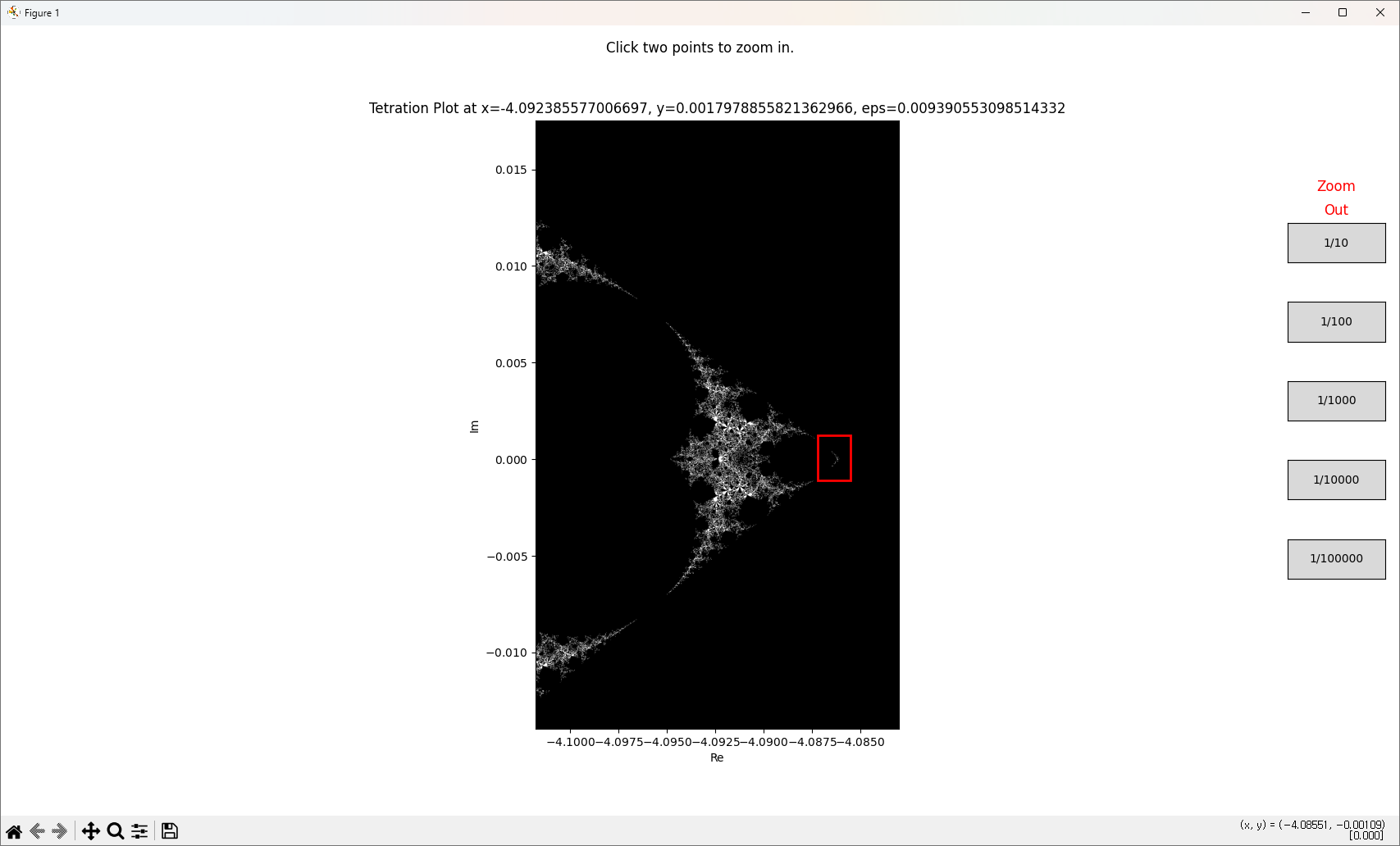
반복
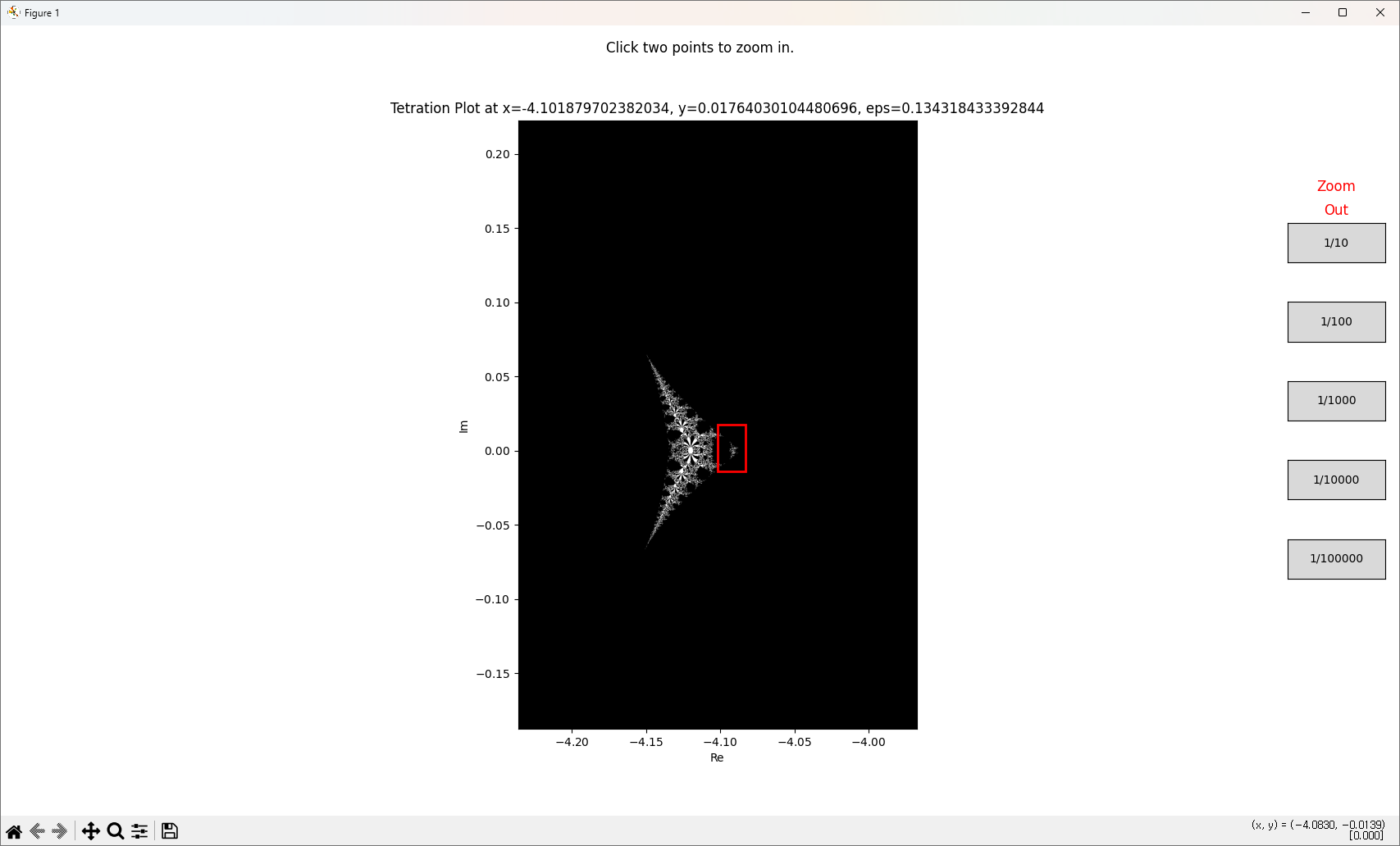
반복하면
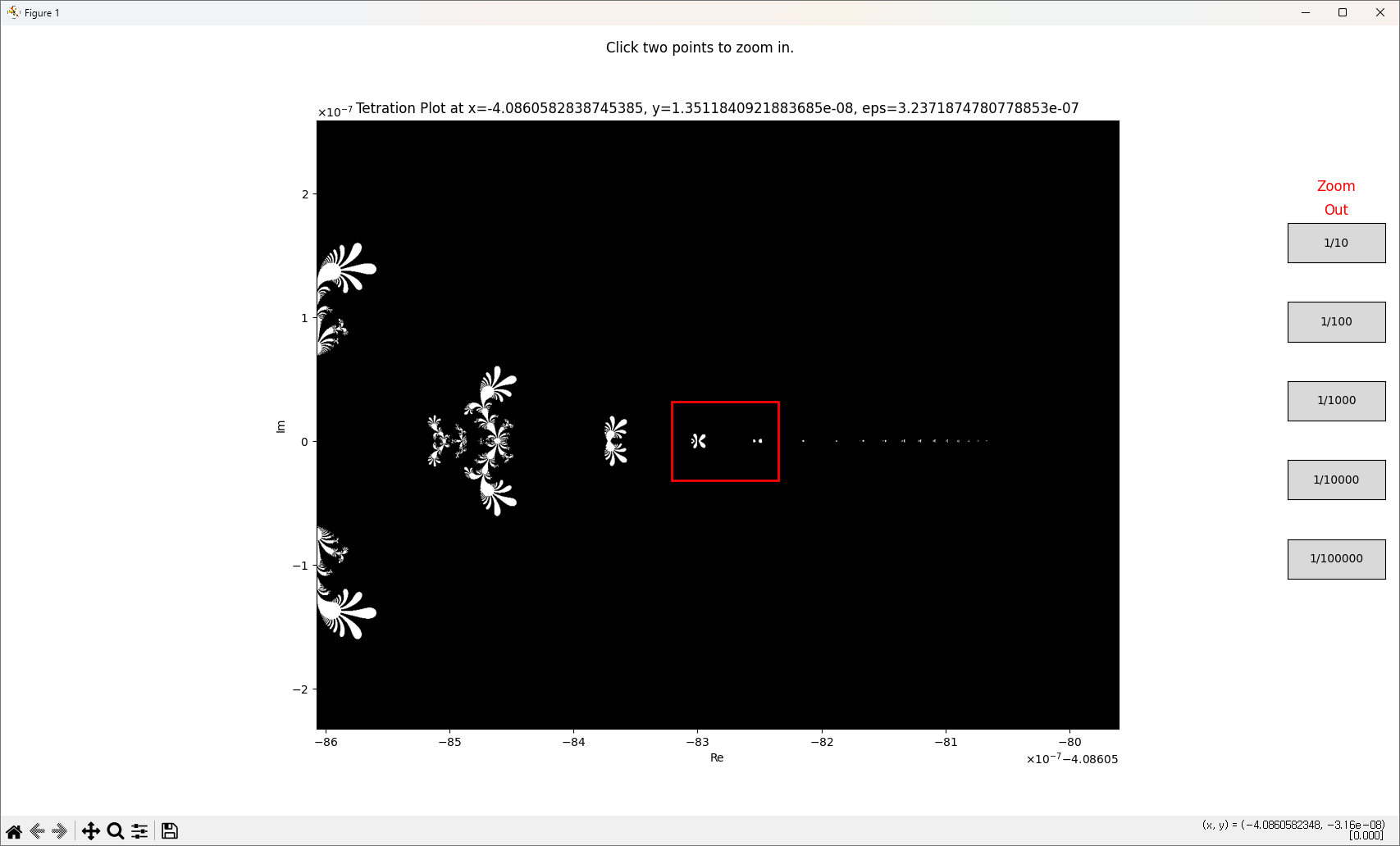
재밌는 패턴을 발견할 수도 있습니다.
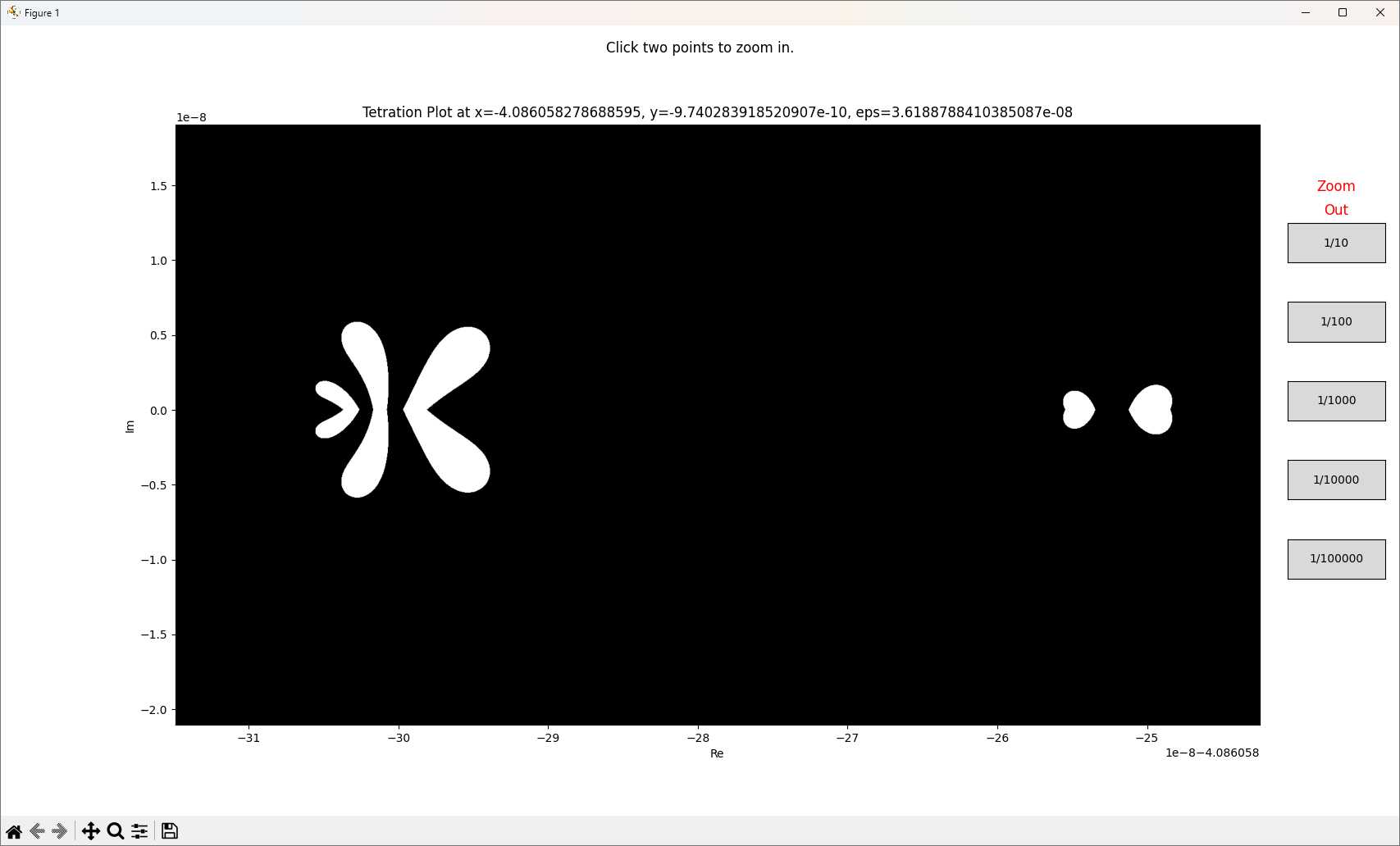
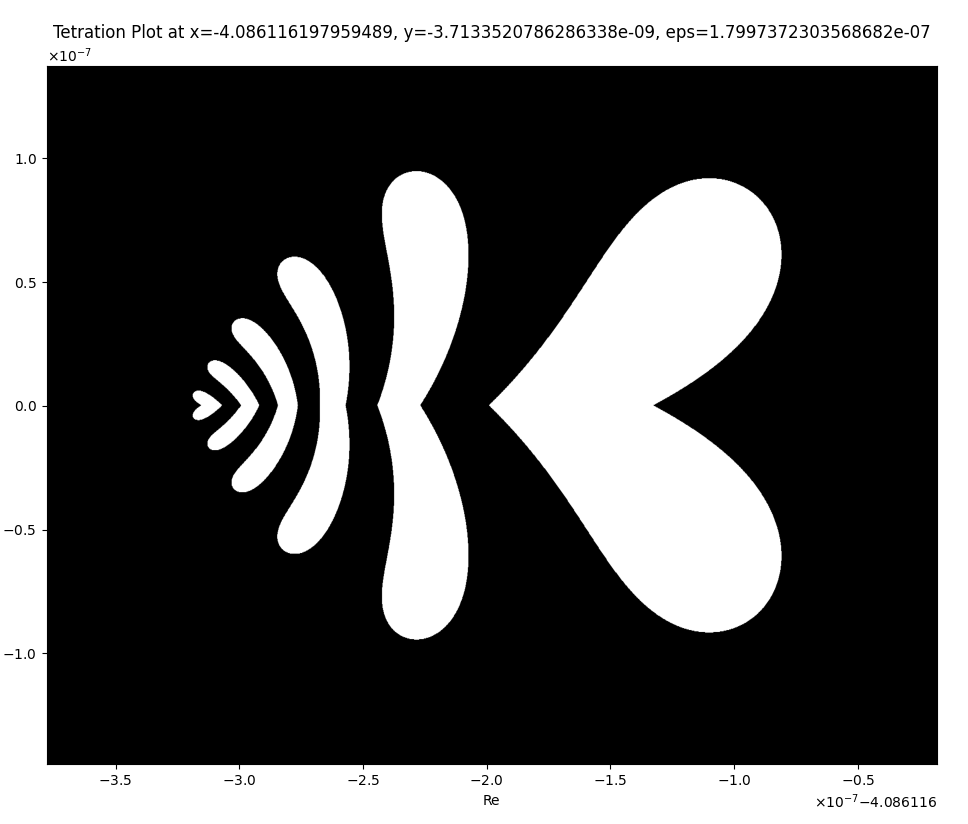
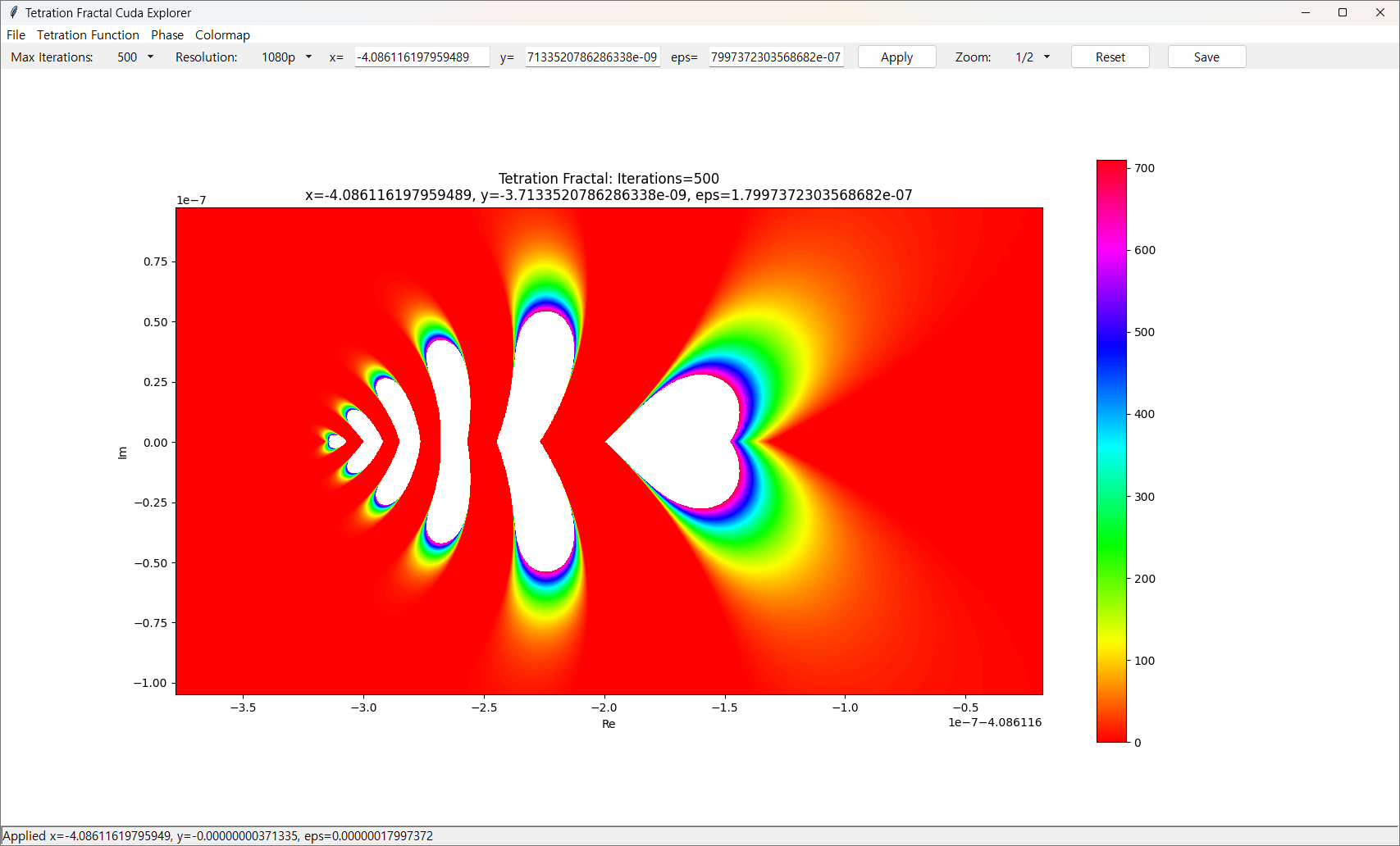
왼쪽은 나비같기도 하고, 하나은행 로고 같기도 하고.
오른쪽은 빼박 하트죠?
좌표
x(Re) = -4.086058278688595
y(Im) = -9.740283918520907e-10
eps = 3.6188788410385087e-08
-
25
세상의모든계산기 님의 최근 댓글
예시11) 선형 연립방정식에서 답이 false 로 나올 때 https://allcalc.org/55823 2025 10.22 approx(참 해) 값이 이상하게 튀는 것 같아서 AI를 이용해 (python 으로) 구해보았습니다. * python 의 유효자릿수가 nspire 의 유효자릿수(14자리~15자리)보다 더 길기 때문에 시도하였습니다. ** 원래는 wolfram alpha 로 구해보려고 했는데, 울프람에서는 수식 길이가 너무 길다고 거부하는 바람에 포기하였습니다. 그 결과, AI approx(참 해) 값은 정상 범주에 포함되었고, 이는 solve()로 구한 대부분의 결과값과 유사하였습니다. 그럼 nspire 의 approx(참 해)는 왜 튀었나? 참 해에 더하기,빼기,곱하기,나누기 가 너무 많이 포함되어 있다보니, 모두 계산하고 나면 오차가 누적&증폭되어 버리는 것 같습니다. 그래서 오히려 solve의 numeric 한 접근보다도 더 큰 오차가 발생한 듯 하고, 그래서 적절한 해의 x 구간을 벗어나버린 듯 합니다. 그것이 처음의 solve 에서 false 를 이끌어낸 주 원인이 아니었을까요? (추정) 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 참 값을 approx() 로 변환한 근사값은 원래 방정식 모두를 만족할 수 없지만, linsolve() 로 찾은 근사값과, AI로 참 값을 근사변환한 값은 원래 방정식 모두를 만족할 수 있습니다. 2025 10.21