[공학용 계산기] C.A.S (카스, CAS) 기능이란?
1. CAS 기능이란?

"C.A.S"는 Computer Algebra System 의 약자입니다.
한국말로 번역하면 계산기 대수학 체계? 정도가 되는데, 영어로든 한국어로든 감이 잘 안오실겁니다.
쉽게 설명해서 CAS 를 지원한다는 것은
"(숫자뿐 아니라) 문자로도 계산이 가능하다"것을 의미합니다.
계산기에 "a × 2a" 라고 입력하여
그 결과가 "2a²" 로 표시될 수 있다면,
그 계산기는 C.A.S 기능을 지원하는 기종입니다.
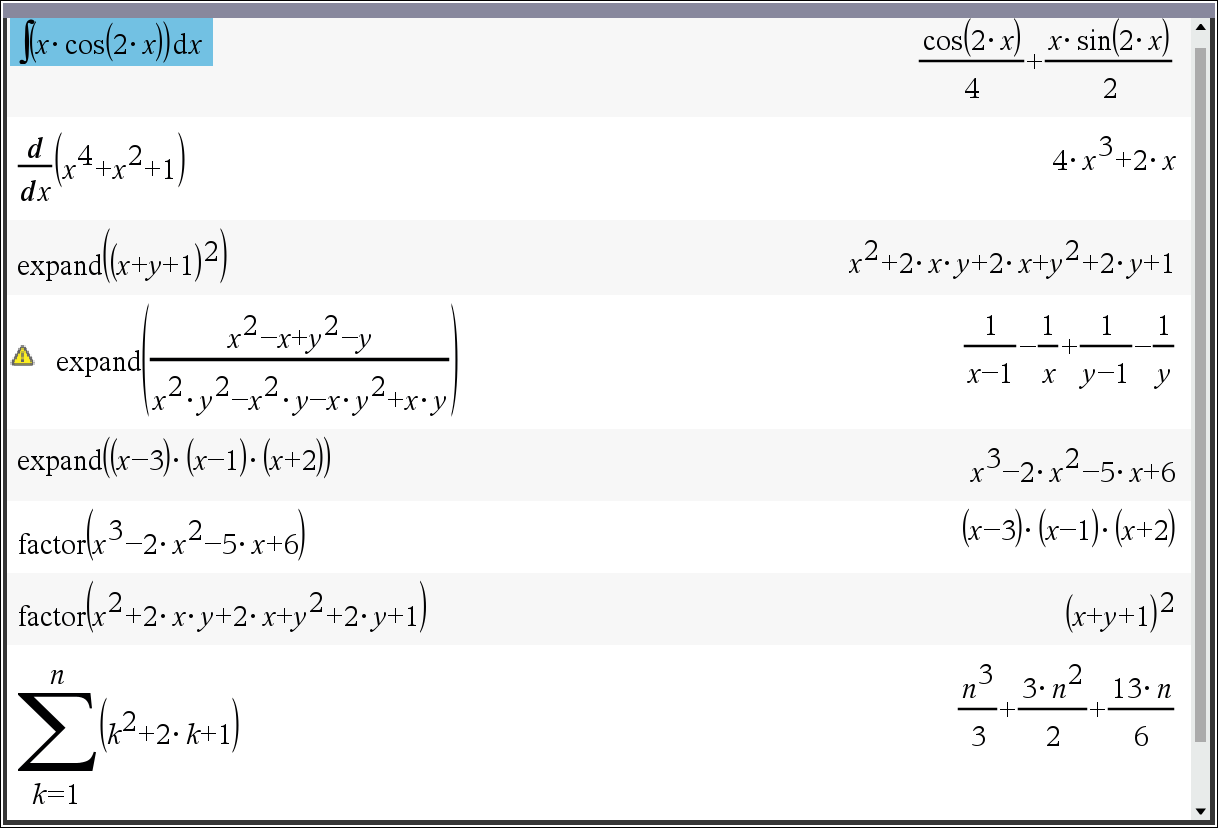
* 대표적인 CAS 기능 : 부정적분, 미분, 다항식의 전개/인수분해, ∑ 등을 이용한 문자 계산
2. 해당 기종
대표적으로 많이 사용되는 보급형 모델인 fx-570 시리즈에는 CAS 기능이 없습니다.
CAS 기능이 있는 공학용 계산기는 대부분 비싸며,
계산기 제조사별로 최상위 모델이 이에 해당합니다.
TI-89 시리즈 (단종)TI-Nspire CAS : 단종TI-Nspire CX CAS : 단종- TI-Nspire CX CAS II : 추천
HP 50G : 단종- HP - PRIME : 추천했었지만... (24년 말 기준 공식 수입업체 없음. 직구 필요)
- CASIO fx-cp400 : 직구필요. 사용자 적음. 비추천
- SHARP - 없음.
- NUMWORKS : 직구필요. 사용자 적음. 비추천
실물 계산기를 꼭 써야하는 상황이 아니라면 인터넷을 이용한 울프람알파가 가장 좋은 CAS 계산기입니다.
위에 소개한 실물 계산기보다도 월등한 성능을 보여줍니다.
- http://www.wolframalpha.com
3. 특징 및 주의사항
- 사용 제한
CAS 계산기는 그 막강한 성능 때문에, 수업 및 시험에서 사용이 제한되는 경우가 많이 있습니다. 따라서 계산기 구매하기 전에 담당자(교수님, 선생님, 담당자, 관리책임자)에게 CAS 계산기 사용이 허용되는지부터 확인하셔야 합니다.
- 가격
CAS 계산기는 가격이 비쌉니다. 최신 기종은 환율 따라 달라지는데 대략 15~25만원 사이입니다. 단종 모델인 경우 가격이 내려가는 경우도 반대로 올라가는 경우도 있습니다.
따라서 본인에게 꼭 필요한 기능인지 검토해보실 필요가 있습니다.
- 복잡함
CAS 급 계산기는 기능이 많습니다. 별의별의별 기능이 다 들어가다보니, 단순 기능만을 사용하는 저가형 계산기보다 오히려 더 불편할 수도 있습니다.
AI처럼 내 생각을 읽어서 풀이를 해주는게 아니므로 어느 정도는 계산기 공부를 하겠다(=시간 비용도 어느 정도 필요함)는 마음가짐 정도는 있어야 합니다.
댓글4
-
-
세상의모든계산기
CAS 공학용 계산기 추천
- 이것저것 살펴봤는데도 복잡해서 잘 모르겠다면
그냥 [TI-Nspire CX II CAS] 를 구입하시면 됩니다. 가격이 부담되면 [HP 50g], 단점(구형에 사용자 부족하여 도움받기 쉽지 않음) // 단종으로 구할 수 없음.- 구형 모델도 상관없다면 [TI-Nspire CAS] 중고,
단점:구형이라 많이 느립니다. - 뭔가 색다른걸 추구하면 HP Prime 도 좋습니다. 오히려 스펙상으로는 최강자일수도...
- 해외 구매 (Amazon, Ebay 등)에 부담이 없는 경우에는 한번 알아보는 것도 도움이 될 듯.
아마존 직구는 11번가에서 구매하시는게 나을 수도 있습니다.
- 이것저것 살펴봤는데도 복잡해서 잘 모르겠다면



세상의모든계산기 님의 최근 댓글
ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28 자게로 이동조치하였습니다. 그리고 이 글의 내용을 정리하여 HP 포럼에 올려두었습니다. https://allcalc.org/55774 [HP Prime] Solve 함수 사용법 2025 10.27 수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17