재무용 계산기란? 재무용 계산기의 특징과 종류
1. 재무용 계산기란?
재무용 계산기는 다양한 재무 관련 계산을 수행하는 데 사용되는 특수 계산기입니다.
따라서, 일반 계산기로는 매우 복잡하게 해야 하는 작업을 단순하게 처리할 수 있고,
일반 계산기로는 불가능한 작업도 재무 계산기 함수로는 계산이 가능한 경우도 있습니다.
2. 재무용 계산기의 특징
재무용 계산기는 일반적인 계산기와는 다른 몇 가지 특징이 있습니다.
주로 재무 관련 작업에 특화되어 있으며, 다음과 같은 기능을 합니다.
1. 시간 가치 (Time Value of Money) : 현재 가치와 미래 가치를 변환하거나, 기간에 따른 가치 변화를 계산합니다.
2. 원금 상환 (Amortization) : 대출 상환 시 월 상환금이나 상환 일정을 계산할 때 유용합니다.
3. 현금 흐름 (Cash Flow) : 투자액이나, 회수액 등의 현금 흐름을 바탕으로 내부 수익률(IRR) 이나 순현재가치(NPV) 등을 계산합니다.
4. 채권 계산 (Bond) : 채권 가격, 만기 수익률(yield to maturity), 콜 수익률(yield to call), 발생 이자(accrued interest), 그리고 수정 듀레이션(modified duration)을 계산합니다.
5. 상각액 계산 (Depreciation) : 원하는 상각 방법을 선택하여, 감가상각 일정을 생성합니다.
6. 통계 (Statistics) : 1-변수 통계, 2-변수 통계, 회귀함수 추출 등의 기능을 합니다.
7. 기타 계산 : 날짜(Date) 계산이나 이자율 변환, 마진율 계산 등 기타 재무 관련 기능이 있습니다.
이와 같은 기능들로 재무용 계산기는 금융 분야에서 매우 중요한 도구로 사용됩니다.
계산기에 따라 특정 기능이 빠지거나 더 추가될 수도 있으니, 설명서를 참고하시기 바랍니다.
3. 재무용 계산기의 종류
- TI :
- TI Business Analyst I (1976)
- TI Business Analyst II (1978)
- BA II Plus
- BA II Plus Professional
- HP :
- HP-12C (1981) :
ㄴ HP-12C 30th Anniversary Edition (NW258AA, 2011) : 40000 개 한정판
ㄴ HP-12C (2015, 복각판) - HP-17B
- HP-19B
- HP-12C Platinum (F2231A, 2003)
ㄴ HP-12C Platinum (F2231AA, 2007) - HP-17BII
- 10B II+
- HP-12C (1981) :
- 3. CASIO :
- SHARP :
- EL-733A (1988)
- EL-738
- EL-738C
- EL-738F
- EL-738XT
4. 시험에서의 활용
재무용 계산기는 강력한 재무 기능을 가지고 있기 때문에,
역설적이게도 재무 관련 시험, 특히 회계사 시험에서는 사용이 금지되어 있습니다.
Q-net 에서 관리하는 기사/기능사 시험에서 허용하는 계산기 리스트 중에서는
재무용 계산기도 없고, 재무 기능이 있는 공학용 계산기도 없습니다.
아마도 대학교 시험에서는 허용이 될 것 같은데, 조교님께 미리 확인해 보셔야 합니다.
수험/시험 목적이신 경우 해당 시험에서 재무용 계산기를 사용할 수 있는지 미리 확인하세요.
시험에 닥쳐서 확인하다가 사용불가 판정을 당하면 매우 난감하실 겁니다.
5. 공학용 계산기와 비교
기본형 공학용 계산기의 경우 재무관련 함수가 구현되어 있지 않습니다. 그래서 재무 관련 계산에는 일반적인 계산식을 그대로 입력해야 합니다.
일반 계산기, 쌀집 계산기와 비교하면 편의성은 그 중간 정도로 볼 수 있을 것 같고, 계산 가능성은 90% 정도로 볼 수 있겠습니다.
반대로 재무용 계산기로는 공학용 계산 일부를 할 수는 있으나, 식 입력에 있어 공학용 계산기보다 많이 불편합니다.
한번 두번 계산이야 할 수 있겠지만, 공학용 계산기의 대용으로 쓴다고 한다면 말릴 겁니다.
고급 공학용 계산기(fx-9860G 시리즈 이상, TI-84, TI-nspire, HP Prime 등등)의 경우,
재무 함수가 기본 기능으로 포함됩니다. 오히려 재무용 계산기보다 더 편리할 수도 있습니다.
재무용 계산기의 가격대는
대략 5만원 내외 정도로 형성되어 있는데, 기본형 공학용 계산기와 (중급) 그래핑 공학용 계산기 중간 가격대 정도입니다.
댓글2
-
세상의모든계산기
2024년 8월 기준으로...
1. 일반적으로 대중적으로 인기 있는 있는 기종은 TI 와 HP 제품입니다.비슷한 비중인 듯 합니다.
2. 카시오 샤프는 잘 안쓰는 편인것 같아요.
3. 가격 면에서는 샤프 제품이 (39000, 무배) 제일 저렴한 편으로 보여지구요.https://prod.danawa.com/info/?pcode=16089023&cate=19238288
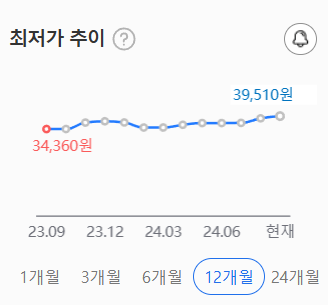
4. 많이 사용해본 건 아닌데
가능한 기능(Function)의 갯수이나 작동방식 편의성(UI)은 고만고만 도토리키재기인 것 같습니다.


세상의모든계산기 님의 최근 댓글
500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28