- 세상의 모든 계산기 수학, 과학, 공학 이야기 확률통계 ()
Coupon collector's problem 쿠폰 수집 문제
https://en.wikipedia.org/wiki/Coupon_collector%27s_problem
카드가 있습니다.
- 카드는 총 n 종류이고, 1회에 1번 카드 덱에서 카드를 받습니다.
(단, 쿠폰을 뽑는 쿠폰박스의 쿠폰 갯수는 무한대로, 이전에 뽑은 쿠폰의 종류에 영향을 받지 않습니다.) - 이 때, 임의의 한 종류 카드가 뽑힐 확률은 1/n 로 모든 종류의 카드가 동일합니다.
- 중복되는 카드는 다른 사람과 교환할 수 없습니다.
질문 :
What is the probability that more than t sample trials are needed to collect all n coupons?
Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once?
모든 종류의 카드를 모으기 위해서,
몇번 정도를 카드를 뽑아야 할 것으로 기대할 수 있는가?


댓글5
-
세상의모든계산기
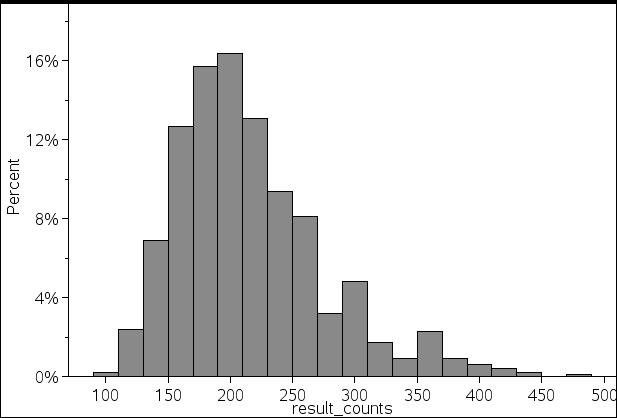
48장의 카드라면
48 * H(48) = 48 * 4.458797175064 = 214.02226440307 회<48장 모으기 시도횟수 샘플, 1000회>

-
세상의모든계산기
ChatGPT-4o mini 답변
이 문제는 고전적인 "Coupon Collector's Problem"에 해당합니다. 이 문제는 주어진 종류의 모든 카드를 수집하는 데 필요한 평균적인 시도를 계산하는 문제입니다. 각 종류의 카드를 한 번씩 수집하는 데 필요한 평균적인 시도 횟수를 구하는 것이 목표입니다.
1. 기대값 계산 (Expected Value)
이 문제를 해결하기 위해서는 각 카드 종류를 수집하는 데 필요한 평균적인 시도 횟수를 계산해야 합니다. 이를 위해 다음과 같은 단계를 따릅니다.
문제 정의
- 총 카드 종류: \( n \)
- 각 카드가 뽑힐 확률: \( \frac{1}{n} \)
- 각 카드가 수집될 때까지의 시도 횟수:\( T_i \)를 \( i \)-번째 새로운 카드가 수집될 때까지의 시도 횟수라고 합시다. \( T_i \)는 기하 분포를 따릅니다. \( i \)-번째 카드가 수집되기까지 \( T_i \)번 시도해야 할 확률은 \( \frac{n}{n - (i - 1)} \)입니다.
기대값 계산
1. 기대값 구하기
- 첫 번째 카드가 수집될 때까지의 시도 횟수는 항상 1입니다.
- 두 번째 카드가 수집될 때까지의 추가 시도 횟수는 \( \frac{n}{n - 1} \)입니다.
- 일반적으로 \( i \)-번째 카드가 수집될 때까지의 추가 시도 횟수는 \( \frac{n}{n - (i - 1)} \)입니다.따라서, 전체 카드 종류를 수집하는 데 필요한 총 시도 횟수의 기대값 \( E[T] \)는 다음과 같습니다:
\[
E[T] = \sum_{i=1}^{n} \frac{n}{i} = n \cdot \left( \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \right)
\]여기서 \( \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n} \)는 \( n \)번째 하르디노 수열 (Harmonic number)로, 약 \( \ln(n) + \gamma \) (여기서 \( \gamma \)는 오일러-마스케로니 상수, 약 0.577)로 근사할 수 있습니다.
따라서:
\[
E[T] \approx n \cdot (\ln(n) + \gamma)
\]2. 확률 계산
특정한 시도 횟수 \( t \)를 초과하여 모든 카드를 수집할 확률을 구하는 것은 좀 더 복잡합니다. 이를 계산하기 위해서는 대개 정확한 확률을 구하기 위한 조합론적 접근과 시뮬레이션을 사용합니다.
예시
- 예를 들어, 10개의 카드 종류가 있을 때, 모든 카드를 수집하는 데 예상되는 시도 횟수는:
\[
E[T] \approx 10 \cdot (\ln(10) + 0.577) \approx 10 \cdot (2.302 + 0.577) \approx 10 \cdot 2.879 = 28.79
\]즉, 평균적으로 약 29번의 시도가 필요합니다.
결론
- 기대값: 모든 종류의 카드를 수집하기 위해서는 평균적으로 약 \( n \cdot (\ln(n) + \gamma) \)번의 시도가 필요합니다.
- 확률: 특정한 시도 횟수 \( t \)를 초과하여 모든 카드를 수집할 확률은 조합론적 접근 또는 시뮬레이션을 통해 계산할 수 있습니다.


세상의모든계산기 님의 최근 댓글
진짜 색약 안경은 비싸서 살 생각은 없고, 알리에서 싸구려 구매해서 테스트 해 봤습니다. 프로그램과 비슷한 효과가 있고, (프로그램과 비교해서) 알리 싸구려 렌즈가 - 숫자 구분이 아주 약간 더 잘 되고 - 붉은 색상이 더 밝습니다. 채도가 높다고 해야하는 것 같네요. 주의할 점은 알리 색약 안경은 일상용으로는 절대 사용 불가입니다. - 내부 빛반사 방지 코팅이 없어서 내 눈알이 렌즈에 비치고, 그래서 실제로 보여야 할 것과 섞여 보입니다. - 필터 코팅도 최악이라서 중심부(=마젠타) 주변부(=노랑)으로 서로 다르게 색이 들어옵니다. 전반적으로 그라데이션 발생. - 외부에서 봤을 때 렌즈색이 튀기 때문에, 티가 많이 납니다. - 색 구분 면에서는 도움이 될 수도 있지만, 녹색(특정 파장)이 차단되어 LED 신호등의 녹색이 잘 안보일 수 있습니다. 2025 12.24 교점이 2개 이상일때 모든 값을 구하는 법 계산기마다 가능/불가능이 갈릴 수도 있습니다. ㄴ fx-570 의 solve 는 무조건 한번에 하나씩 찾습니다. 따라서, 2차 3차 방정식처럼 규격화된 수식은 solve 대신 EQN 모드에서 답을 구하는게 좋습니다. ㄴ TI-nspire 같은 CAS 계산기의 solve 는 수식에 따라서 여러개가 한꺼번에 찾아지기도 합니다. https://allcalc.org/3448 ㄴ fx-9860G 의 solve는 무조건 1개, solveN 는 수식에 따라 여러개가 찾아질 수 있습니다. https://allcalc.org:443/board_casio/6005#comment_15889 가능하다면, 불확실할때는 그래프로 확인하세요. 2025 12.16 T가 410인 해를 찾는 방법 -> 초기값을 입력하세요. [공학용 계산기] 공학용 계산기의 꽃? solve (솔브) 기능 이해하기 (Newton-Raphson 법, 뉴튼법) https://allcalc.org/11532 2025 12.16 참고 - [공학용 계산기] 정적분 계산 속도 벤치마크 비교 https://allcalc.org/9677 2025 12.11 다른 계산기의 경우와 비교 1. TI-nspire CAS ㄴ CAS 계산기는 가능한 경우 부정적분을 먼저하고, 그 값에 구간을 대입해 최종값을 얻습니다. ㄴ 부정적분이 불가능할 때는 수치해석적 방법을 시도합니다. 2. CASIO fx-991 ES Plus ㄴ CASIO 계산기의 경우, 적분할 함수에 따라 시간이 달라지는 것으로 알고 있는데, 정밀도를 확보할 별도의 알고리즘을 채택하고 있는 것이 아닐까 생각되네요. 2025 12.11