- 세상의 모든 계산기 수학, 과학, 공학 이야기 수학 ()
변곡점(變曲點, inflection point)
변곡점의 정의
변곡점(變曲點, inflection point)은 곡선의 곡률이 부호를 바꾸는 점을 말합니다.
좀 더 구체적으로, 곡선 \( y = f(x) \)에 대해 다음 두 조건을 모두 만족하는 점 \( (a, f(a)) \)을 변곡점이라고 합니다:
1. \( f''(a) = 0 \) 또는 정의되지 않는다.
2. \( f''(x) \)가 \( x = a \)를 기준으로 좌우에서 부호가 바뀐다. 즉, \( x < a \)일 때 \( f''(x) \)와 \( x > a \)일 때 \( f''(x) \)의 부호가 다르다.
이를 통해 변곡점에서 곡선의 오목(콘케이브)과 볼록(컨벡스)의 특성이 바뀌게 됩니다.
예를 들어, \( y = x^3 \) 함수는 \( x = 0 \)에서 변곡점을 가집니다. 왜냐하면,
- \( f''(x) = 6x \)이고,
- \( f''(0) = 0 \)이며,
- \( x = 0 \)의 좌우에서 \( f''(x) \)의 부호가 바뀌기 때문입니다. \( x < 0 \)일 때 \( f''(x) < 0 \), \( x > 0 \)일 때 \( f''(x) > 0 \)입니다.
이러한 변곡점을 찾기 위해 2차 도함수 테스트(Second Derivative Test)를 사용하기도 합니다. 변곡점의 위치를 정확히 알아내기 위해서는 함수의 도함수를 계산하고 그 값을 분석하는 과정이 필요합니다.
특징
- 연속성: 변곡점에서 함수는 연속이어야 합니다.
- 미분 가능성: 변곡점에서 함수는 최소한 1차 미분 가능해야 합니다.
- 곡률 변화: 변곡점을 기준으로 함수의 곡률(curvature)이 바뀝니다. 즉, 그래프의 오목성(concavity)이 변화합니다.
- 접선의 특성: 변곡점에서의 접선은 함수 그래프를 관통합니다. 이 점을 제외한 다른 점에서는 접선이 함수 그래프와 한 점에서만 만납니다.
- 2차 도함수와의 관계: 대부분의 경우, 변곡점에서 2차 도함수(f''(x))가 0이 됩니다. 그러나 2차 도함수가 존재하지 않는 경우에도 변곡점이 될 수 있습니다.
- 3차 도함수의 역할: 만약 2차 도함수가 0이라면, 3차 도함수를 확인하여 실제로 변곡점인지 판단할 수 있습니다. 3차 도함수가 0이 아니라면 그 점은 변곡점입니다.
댓글2
-
세상의모든계산기
"4차 함수의 변곡점이 존재한다면, 그 도함수는 반드시 극대, 극소값을 가진다."라는 명제는 참인가?
### 명제
"4차 함수의 변곡점이 존재한다면, 그 도함수는 반드시 극대, 극소값을 가진다."
### 증명
1. **전제:**
- 4차 함수 \( f(x) = Ax^4 + Bx^3 + Cx^2 + Dx +E, (A \neq 0) \)의 변곡점이 존재한다.2. **변곡점의 조건:**
- 변곡점 \( a \)에서 \( f''(a) = 0 \)이면서, \( a \)의 좌우에서 \( f''(x) \)의 부호가 바뀐다.3. **2차 도함수 \( f''(x) \):**
- \( f''(x) \)는 4차 함수 \( f(x) \)의 두 번째 도함수로서 2차 함수의 형태이다.
- 따라서 \( f''(x) \)는 다음과 같은 형태를 가진다:
\[ f''(x) = 12Ax^2 + 6Bx + 2C \]
여기서 \( A \neq 0 \)이고, \( A \), \( B \), \( C \)는 4차 함수의 계수에 따른 상수이다.4. **2차 방정식의 성질:**
- \( f''(x) = 0 \)을 만족하는 \( α \)가 존재하고, \( α \)의 좌우에서 \( f''(x) \)의 부호가 바뀌므로 \( f''(x) = 0 \)을 만족하는 또 다른 실근 \( β \)가 반드시 존재해야 한다.
- 이는 2차 방정식 \( f''(x) = 0 \)이 서로 다른 두 실근 \( α \)와 \( β \)를 가진다는 것을 의미한다.5. **1차 도함수 \( f'(x) \):**
- \( f'(x) \)는 4차 함수 \( f(x) \)의 첫 번째 도함수로서 3차 함수의 형태이다.
- 3차 함수 \( f'(x) \)는 \( f''(x) = 0 \)이 되는 점 \( α \)와 \( β \)에서 극값(극대,극소 or 극소,극대)을 가진다.6. **결론:**
- 3차 함수 \( f'(x) \)는 극대값과 하나의 극소값을 가진다.
- 따라서, 4차 함수의 변곡점이 존재한다면, 그 도함수인 3차 함수 \( f'(x) \)는 반드시 극대와 극소값을 가진다. -
1
세상의모든계산기
반례) f'(x) = a*(x-α)*(x-β)^2 형태인 경우 ?
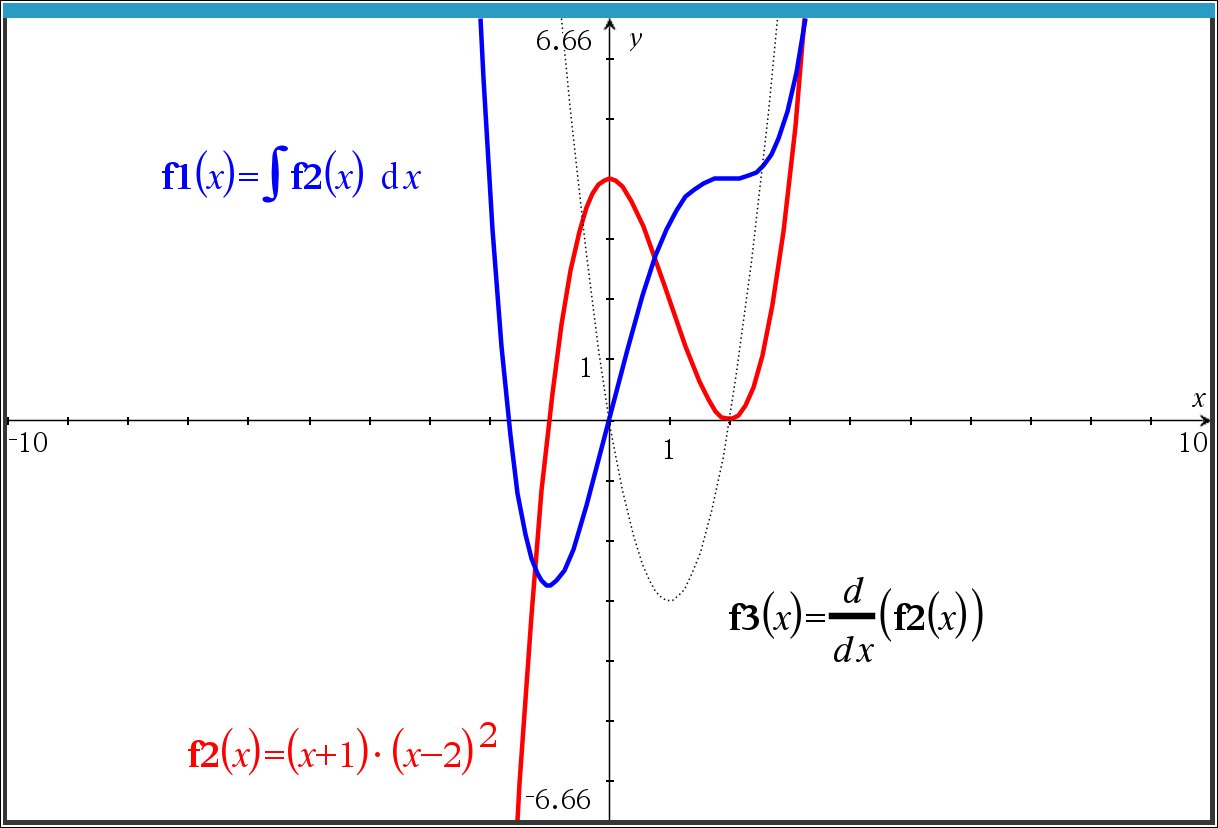
3차함수 f2(x) 는 극대, 극소를 모두 가짐.
따라서 반례 실패.
"4차함수가 극대/극소를 모두 가지는지 물은 것이 아님"


세상의모든계산기 님의 최근 댓글
낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10 마지막 발언이 마지막 힌트이자 문제의 핵심이군요. 처음 들은 달이 8월이었다면 (15일인지 17일인지 확신할 수 없어서) 마지막 대사를 할 수 없지만, 처음 들은 달이 7월이었다면 (선택지가 16일 하나라서 확신이 가능하므로) 마지막 대사를 할 수 있다. 대사를 했으니 7월이다. 이제 이해되었습니다. 지금 보니까 이해가 되는데, 당시에는 왜 이해가 안됐을까요? 세가지 전제 하에 문제를 풀면 A는 마지막 대화 2줄만으로 C의 생일을 알 수 없어야 정상인데, 무슨 이유에서인지 "그럼 나도 앎!"이라고 선언해 버립니다. 알게 된 이유를 대화 속에서 찾을 수는 없습니다. 이 편견에 사로잡혀 빠져나오지 못하고 다른 길로 계속 샜나봅니다. 2025 10.09 (장*훈)님 (+10,000원) 계좌 후원(2025/10/09) 감사 드립니다. 2025 10.09 원래 식이 풀어진 상태에서는 두번째 인수 v가 분모, 분자에 섞여 있어서 계산기가 처리하지 못하는 듯 합니다. 이 때는 위에서와 반대로 분모 부분만 다른 문자(w)로 치환한 다음 completesquare(,v^2) 처리를 하면 일부분은 묶이는 듯 합니다. 하지만 여기서 처음 모양으로 더 이상 진행되진 않네요. 2025 10.08 전체 식에서 일부분(분모, 루트 내부)만 적용할 수는 없습니다. 번거롭더라도 해당 부분만 따로 끄집어 내서 적용하셔야 합니다. https://allcalc.org/30694#comment_30704 2025 10.08