- HP HP Prime
HP-39gs 에 대하여
!주의!
댓글로 알려주신 유저분(미나미 님)의 정보에 따르면 알리 구입품이 진품이 아닐 가능성이 있어 보입니다.
설령 진품이라 하더라도 상태가 좋지 않은 진품일 수 있습니다. 해외 직구시 구매평을 꼼꼼히 읽어보시고 구입에 주의하시는게 좋겠습니다.
[추가 21-07-24]
비슷한 등급의 CASIO fx-9750GIII 를 (아마존, 이베이 등에서) 배송비 포함해 $50 아래로 구입할 수 있는 상황입니다.
따라서 HP-39GS보다는 fx-9750GIII 쪽을 더 추천합니다.

1. 가격
알리 익스프레스를 서핑하던 중 HP-39gs 를 보았는데 가격이 US $18.49(무배, 13~21일)로 매우 낮아서 급관심이 갔습니다.
네이버에서 검색해 보니 케이스 없는(아마도 벌크) 제품이 43,650원에 판매중이더라구요. (최저가)
http://11st.kr/QR/P/1442792279
상품 사진상 그래핑이 가능한 것으로 보이는데, 과연 어느 급의 계산기일지, 상세한 성능에 대해 간략히 알아 보았습니다.
유저 메뉴얼 : http://h10032.www1.hp.com/ctg/Manual/c00045564.pdf
[2024년 9월 내용 추가]
현재는 알리든 국내에서 직구하는 거든 관계없이 저렴한 제품은 없습니다. 가격대가 6만~7만원 정도 하는 상황입니다.
진품인지도 확신할 수 없는 상황이므로 구입할 가치가 없습니다.
2. 성능
- 사칙연산, 지수/로그, 삼각함수 ㅇ
- 통계 ㅇ, 분포 ㅇ
- 정적분, 미분계수 ㅇ
- 복소수 ㅇ
- 행렬 ㅇ (최대?)
복소수 행렬 ㅇ
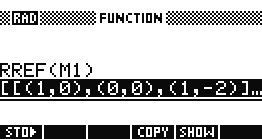
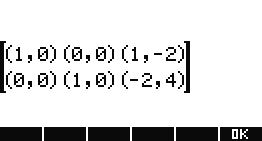
- 벡터 O
- 공식 저장 ㅇ
(Function Applet ㅇ)
- 프로그래밍 ㅇ
- 그래핑 ㅇ
- 재무 함수 ? (없는 듯)
TVM Solver (Applet) ㅇ

- C.A.S ? △
Symbolic calculations 이라는 기능이 있습니다.
하지만 최신의 C.A.S 계산기와 같은 성능으로 보긴 어려운 것 같습니다.간단한 기호 연산?
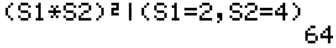
간단한 미분
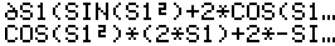
간단한 부정적분
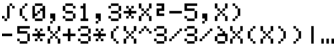
└ 보시는 것처럼 깔끔하게 처리되는 것은 아닙니다.
3. 총평
그래핑 급(예 : fx-9860G 시리즈나 TI-84급) 계산기로는 충분합니다. CAS 기능은 일부 있지만 크게 기대할 수준은 아닌 것 같구요. 직구로 A/S 포기한 가격이 2만원 초반대라면 매우 메리트 있어 보입니다. 국내 쇼핑몰 최저가인 43650원(케이스 없는 벌크)도 경쟁 제품(카시오 9860G 시리즈)과 비교하면 메리트 있어 보입니다. 다만 국내 A/S 가능한 제품인지는 불확실해 보입니다.
"fx-570 급으로는 뭔가 부족하고, fx-9860G 사기엔 돈아깝다"고 생각될 때 대안으로서 적절해 보입니다.
다만, 적은 사용자 수, 고장시 A/S가 어렵다는 점, 알리의 느린 해외(무료)배송 등이 걸림돌로 남습니다.
댓글7
- 1
- 1
-
세상의모든계산기
HP 39 series 변천사
39g
(F1906A)39g+
(F2224A)39gs
(F2223A)39gII
(NW249AA)출시일 2000 2003 2006 2011 CPU 4MHz Yorke
(Saturn core)75MHz
(ARM920T Core)75MHz
(ARM920T Core)80MHz
(ARM926EJ-S Core)RAM / Flash 256KB / - 256KB / 1MB 256KB / 1MB 256KB / 128MB Screen 131×64 131×64 131×64 256×128 특징 39g와 OS 동일.
Saturn 칩을 에뮬로 동작시킴.
ㄴ 하지만 더 빠름수학 라이브러리
갈아 엎음.
System RPN으로부터 독립적임.
실험적? 작품으로
각종 bug가 고쳐지지 않음.* 자료 출처
https://en.wikipedia.org/wiki/HP_39/40_series


세상의모든계산기 님의 최근 댓글
수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17 Gemini-2.5-pro 답변 ✦ 현대 컴퓨터 대수 시스템(CAS) 계산기에 탑재된 solve 기능의 일반적인 내부 동작 원리에 대해 설명해 드리겠습니다. 현대 CAS의 solve 기능은 단순히 하나의 알고리즘으로 작동하는 것이 아니라, 마치 '순수 수학자'와 '문제 해결 공학자'가 협력하는 것처럼, 여러 단계에 걸친 정교한 '하이브리드(Hybrid)' 방식으로 동작합니다. solve 함수의 작동 과정 1단계: 기호적 해법 (Symbolic Solver) - '순수 수학자'의 접근 계산기는 가장 먼저 방정식을 대수적으로, 즉 정확한 수학적 해를 찾으려고 시도합니다. 이 단계는 마치 사람이 공식을 이용해 문제를 푸는 과정과 같습니다. 1. 방정식 분석: solve 명령을 받으면, 시스템은 먼저 입력된 방정식의 구조를 분석합니다. (예: 이것이 다항식인가? 삼각방정식인가? 로그방정식인가?) 2. 규칙 기반 풀이: 분석된 구조에 따라, 시스템은 내장된 방대한 수학 규칙 라이브러리를 적용합니다. * 선형/이차 방정식: ax+b=c 나 ax²+bx+c=0 같은 형태는 이항, 인수분해, 근의 공식 등을 이용해 즉시 풉니다. * 고차 다항식: 인수분해, 조립제법 등의 규칙을 적용하여 유리수 해를 찾습니다. * 삼각방정식: sin(x) = 0.5 와 같은 경우, x = nπ + (-1)ⁿ * (π/6) 와 같이 주기성을 고려한 일반해 공식을 적용합니다. * 기타: 로그, 지수 법칙 등 해당 방정식에 맞는 대수적 풀이법을 총동원합니다. 3. 결과: 이 단계에서 해를 찾으면, 1.414... 와 같은 근사값이 아닌 √2 나 π/3 와 같은 정확한 기호 형태의 해를 반환합니다. > 강점: 수학적으로 완벽하고 정확한 해를 제공합니다. > 한계: 대수적인 풀이법이 알려져 있지 않은 방정식(예: cos(x) = x 또는 eˣ = x+2)은 풀 수 없습니다. --- 2단계: 수치적 해법 (Numerical Solver) - '문제 해결 공학자'의 접근 만약 1단계의 '순수 수학자'가 "이건 공식으로 풀 수 없어"라고 결론 내리면, solve 기능은 포기하지 않고 2단계인 '문제 해결 공학자'에게 문제를 넘깁니다. 이 단계의 목표는 정확한 해는 아니더라도, 매우 정밀한 근사해를 찾는 것입니다. 1. 반복적 탐색: 수치적 해법은 방정식을 직접 푸는 것이 아니라, 해가 있을 만한 지점에서부터 시작하여 반복적인 계산을 통해 해에 점점 더 가까워지는 방식을 사용합니다. * 적당한 값을 추측해서 대입해 봅니다. * 결과가 0보다 큰지 작은지에 따라, 다음 추측값을 어느 방향으로 수정할지 결정합니다. * 이 과정을 수없이 반복하여 오차가 거의 0에 가까워질 때까지 해를 좁혀나갑니다. 2. 핵심 알고리즘: 이때 사용되는 대표적인 알고리즘은 다음과 같습니다. * 뉴턴-랩슨법 (Newton-Raphson Method): 미분(접선)을 이용하여 매우 빠른 속도로 해에 수렴하는 강력한 방법입니다. * 이분법 (Bisection Method): 해가 존재하는 특정 구간을 계속 절반으로 나누어 범위를 좁혀나가는 방식으로, 속도는 느리지만 안정적으로 해를 찾을 수 있습니다. 3. 결과: 이 단계가 성공하면, 시스템은 0.739085133215 와 같이 소수점 아래 여러 자리까지 표현되는 매우 정밀한 부동소수점 형태의 근사해를 반환합니다. > 강점: 대수적으로 풀 수 없는 복잡한 방정식의 해도 근사적으로 찾아낼 수 있습니다. > 한계: 근사해이며, 알고리즘의 특성상 특정 조건(예: 해가 중근을 갖는 경우)에서는 해를 찾지 못하고 실패할 수도 있습니다. 결론: 왜 하이브리드 방식인가? 분석 → 기호적 풀이 시도 → (실패 또는 불가능 시) → 수치적 풀이로 전환 이처럼 현대 CAS의 solve 기능은 정확성(기호적 해법)과 범용성(수치적 해법)이라는 두 마리 토끼를 모두 잡기 위해 설계된 정교한 협력 시스템입니다. 먼저 가장 이상적인 '정확한 해'를 추구하되, 그것이 불가능할 경우 차선책으로 '정밀한 근사해'라도 찾아내어 사용자에게 최대한의 결과를 제공하는 것입니다. 2025 10.17 hp prime 이 solve 함수에서 해를 찾는데 어떤 방법(method)을 사용하는지 공식적인 무서로 정확하게 파악되진 않습니다. 2025 10.17 참고 x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을 x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯? 2025 10.17