- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
안티로그 Antilog 가 뭐지?? 첨 들어봤넹...
웹을 검색하다가 "안티로그"라는 단어를 처음 보게 되었습니다.

뭔가 로그에 대한 비난을 쏟아낼 것 같은 느낌이 들어서 움찔했는데,
그냥 '상용로그의 역함수'이더라구요.
(간혹 자연로그의 역함수로 설명하기도 합니다. 그냥 로그의 역함수로 보면 될 듯.)
![]() 괜히 쫄았네.ㅎ
괜히 쫄았네.ㅎ
"Antilog"는 수학에서 로그의 역연산을 의미합니다.
기본적으로 로그는 어떤 수가 특정한 밑에 대해 몇 번 곱해져서 다른 수가 되는지 찾는 과정입니다.
이때 antilog는 그 과정을 거꾸로 하는 작업으로, 주어진 로그 값으로부터 원래의 숫자를 구하는 것입니다.
예시
- 만약 우리가 \( \log_{10}(x) = 2 \)라는 값을 가지고 있다면, 이는 10을 몇 번 곱했을 때 \(x\)가 되는지 알려줍니다.
- \( \log_{10}(x) = 2 \)는 \( x = 10^2 \), 즉 \( x = 100 \)이 됨을 의미합니다.
- 이때 \(100\)을 "antilog"라고 부를 수 있습니다.
일반식
주어진 로그 값 \( y \)에 대해, 밑 \( b \)에 대한 antilog는 \( b^y \)입니다.
- 예를 들어, \( y = 3 \)이고 \( b = 2 \)인 경우, antilog는 \( 2^3 = 8 \)이 됩니다.
계산기에서 antilog 사용
일반 계산기에서는 보통 \(10^x\) 또는 \(e^x\) 키를 사용하여 10진수나 자연 로그의 antilog를 계산할 수 있습니다.
댓글4
-
세상의모든계산기
Logarithm Table (로그 테이블)
https://maths.forkids.education/antilog-log-table-how-to-use-see-value/
Download Print-Friendly PDF Version:
File 1 (1 to 50)
and
File 2 (51 to 99)
-
세상의모든계산기
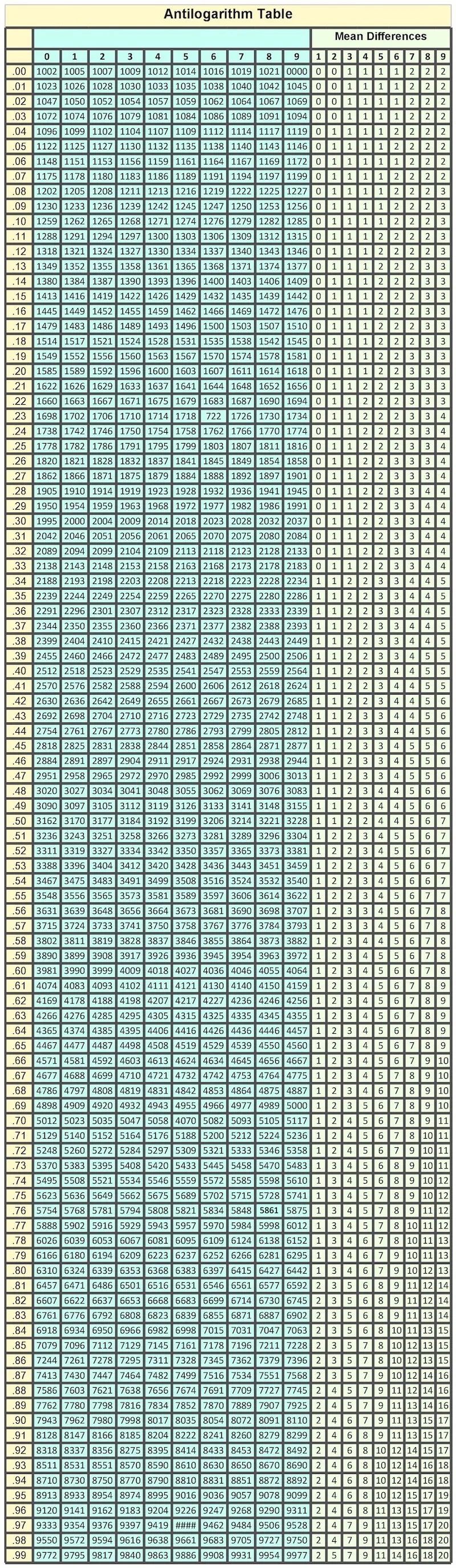
Antilogarithm Table (안티로그 테이블)
Download Print Friendly Antilog Table PDF File:
and
-
세상의모든계산기
log(k)= 1.5629228687415 에서 k 를 구할 때
말씀하신 내용을 반영하여 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 정확하게 찾는 방법을 다시 설명드리겠습니다.
1. 정수 부분과 소수 부분 분리:
\[
\log_{10}(k) = 1.5629228687415
\]
여기서 정수 부분은 1이고, 소수 부분은 0.5629228687415입니다.2. 소수 부분을 두 자리로 반올림:
소수 부분 0.5629228687415을 두 자리로 반올림하면 0.56이 됩니다.3. 안티로그 표에서 0.56 찾기:
안티로그 표의 세로축에서 0.56을 찾습니다. 해당 행에서 첫 번째 열의 값은 3631입니다.
4. 소수 부분의 세 번째 자리 반영:
소수 부분의 세 번째 자리는 2입니다. 0.56 행의 두 번째 열(0.562에 해당)을 찾아야 합니다. 이 값은 3648입니다.5. 소수 부분의 네 번째 자리 반영:
소수 부분의 네 번째 자리는 9입니다. Mean Differences 열에서 9에 해당하는 값을 찾습니다. 이 값은 8입니다.6. 값 더하기:
안티로그 표의 0.562에 해당하는 값인 3648에 Mean Differences의 9에 해당하는 값 8을 더합니다:
3648 + 8 = 3656안티로그표의 값은 원래의 값을 1000배 한 값이므로, 원래값은 ÷1000 으로 구할 수 있습니다.
따라서 소수부분에 해당하는 값은 $ 10^{0.5629228687415} = 3.656 $ 입니다.
7. 정수 부분 반영:
\[
k = 10^{1.5629228687415} = 10^1 \times 10^{0.5629228687415}
\]정수 부분 1을 반영하기 위해 \(10^1\)을 곱합니다:
\[
k = 10^1 \times 3.656 = 10 \times 3.656 = 36.56
\]따라서 최종적으로 주어진 로그 값 \(\log_{10}(k) = 1.5629228687415\)에서 \(k\) 값을 구하면, \(k \approx 36.56\)이 됩니다.


세상의모든계산기 님의 최근 댓글
고장남 - POST 진입 실패, 모니터 안나옴 직접 사용할 일이 없어져서, 고향집에 가져다 놓고 어댑터만 꼽아 두었습니다. 마지막으로 켠 것은 25년 6월쯤이 아니었을까 싶습니다. (이상증상은 없었구요) 이번 추석에 가서 켜 보니까, 화면이 아예 안나오더라구요. 집에 가져와서 분해해 살펴보니까 - 어댑터 12V는 정상 - 어댑터 꼽으면 바로 POWER 는 켜집니다. ㄴ POWER ON -> Fan 돌아감 + 파워 LED 들어옴 + NVME에 LED 들어옴 ㄴ HDMI 1, 2 신호 전혀 안들어옴 (모니터 2대 확인) ㄴ 키보드에 LED 안들어옴 (USB 5V 가 안들어오는 듯 함) - 옆구리 버튼은 작동하지 않습니다. 길게 눌러도 꺼지지 않음. 하나씩 제거하면서 변수를 제거해 봤는데, 뭘 해도 상태가 똑같습니다. 보드쪽에 문제가 생긴 것 같습니다. 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14 낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10