선박의 아웃리거에 의한 선박 안정성(요동 감쇄)
Reduction Of Outrigger Wide To Maximize Fishing Boat ...
https://iptek.its.ac.id › article › download › pdf_266
2024. 8. 5. — Moreover, broader outriggers can amplify vessel motion, leading to extended oscillation periods, ... of the boat with and without the use ...
1. 연구 배경:
- 프리기 지역의 주깅(Jukung) 어선들은 넓은 아웃리거(약 5미터) 때문에 해안 가까이 정박하기 어려운 문제가 있습니다.
2. 연구 목적:
- 아웃리거 폭을 줄여 PPN 프리기 항구의 정박 용량을 늘리면서도 선박 안정성을 유지하는 방법을 찾고자 합니다.
3. 연구 방법:
- 다양한 아웃리거 폭(1.5m, 1.25m, 1m, 0.75m)에 대해 선박 안정성을 분석했습니다.
- HSC 2000 Annex 7과 Annex 749 (18) Ch3 설계 기준을 사용했습니다.
4. 주요 결과:
- 아웃리거 폭을 1미터로 줄여도 선박 안정성 기준을 충족합니다.
- 이 변경으로 15미터 정박지에서 정박 효율을 66% 높일 수 있습니다.
- PPN 프리기 동쪽 부두의 주깅 선박 수용량이 142척에서 236척으로 증가합니다.
5. 결론:
- 아웃리거 폭을 줄이면 항구 인프라를 최적화하고 프리기 어업 공동체의 운영 효율성을 향상시킬 수 있습니다.
이 연구는 전통적인 어선 설계를 현대화하여 항구 용량과 효율성을 개선하는 방법을 제시하고 있습니다.
댓글2
-
세상의모든계산기
클로드 Sonnet 3.5에게 수치적으로 분석해 달라고 했습니다.
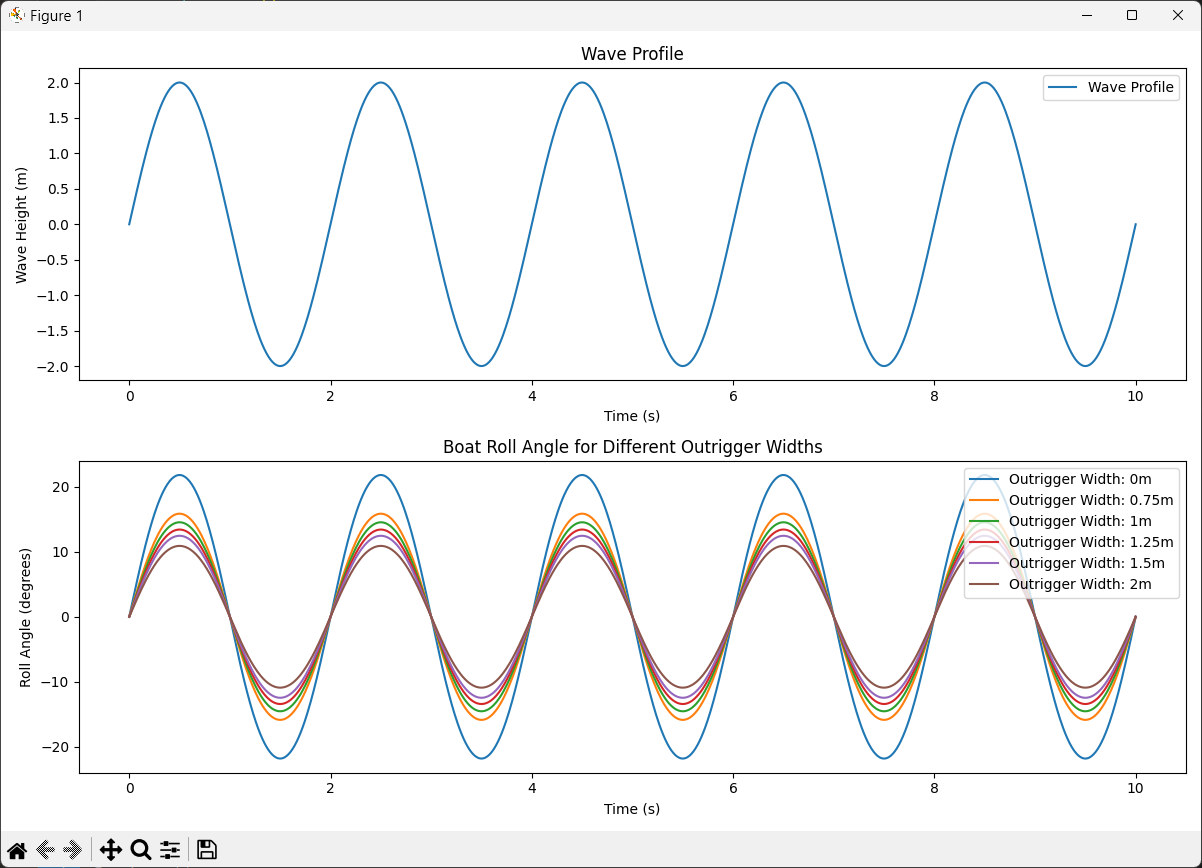
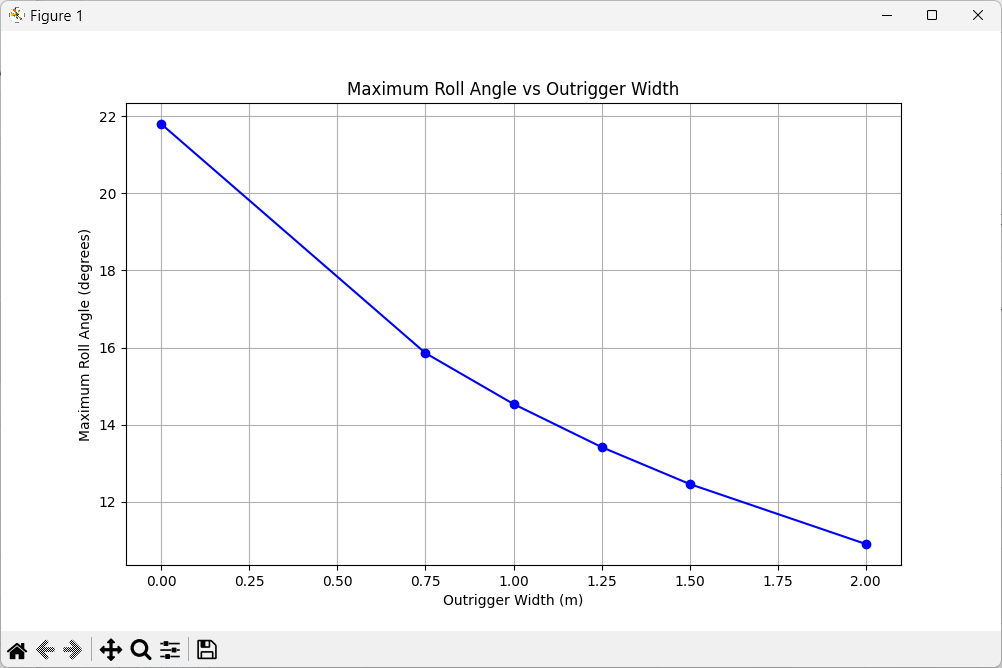
import numpy as np import matplotlib.pyplot as plt from scipy.signal import find_peaks # 파도 프로파일 생성 함수 def generate_wave_profile(time, amplitude, frequency): return amplitude * np.sin(2 * np.pi * frequency * time) # 선박 요동 각도 계산 함수 def calculate_boat_angle(wave_height, outrigger_width): base_angle = np.arctan(wave_height / 5) # 기본 각도 (아웃리거 없을 때) if outrigger_width == 0: return np.degrees(base_angle) else: return np.degrees(base_angle / (1 + outrigger_width * 0.5)) # 아웃리거 효과 # 파라미터 설정 time = np.linspace(0, 10, 1000) # 10초 동안 1000개 데이터 포인트 wave_amplitude = 2 # 파도 진폭 (미터) wave_frequency = 0.5 # 파도 주파수 (Hz) # 파도 프로파일 생성 wave_profile = generate_wave_profile(time, wave_amplitude, wave_frequency) # 아웃리거 폭 범위 설정 outrigger_widths = [0, 0.75, 1, 1.25, 1.5, 2] # 그래프 설정 plt.figure(figsize=(12, 8)) # 파도 프로파일 플롯 plt.subplot(2, 1, 1) plt.plot(time, wave_profile, label='Wave Profile') plt.title('Wave Profile') plt.xlabel('Time (s)') plt.ylabel('Wave Height (m)') plt.legend() # 선박 요동 각도 플롯 plt.subplot(2, 1, 2) for width in outrigger_widths: boat_angles = [calculate_boat_angle(h, width) for h in wave_profile] plt.plot(time, boat_angles, label=f'Outrigger Width: {width}m') plt.title('Boat Roll Angle for Different Outrigger Widths') plt.xlabel('Time (s)') plt.ylabel('Roll Angle (degrees)') plt.legend() plt.tight_layout() plt.show() # 최대 요동 각도 분석 max_angles = [] for width in outrigger_widths: boat_angles = [calculate_boat_angle(h, width) for h in wave_profile] peaks, _ = find_peaks(boat_angles) max_angle = np.mean(np.array(boat_angles)[peaks]) max_angles.append(max_angle) # 최대 요동 각도 플롯 plt.figure(figsize=(10, 6)) plt.plot(outrigger_widths, max_angles, 'bo-') plt.title('Maximum Roll Angle vs Outrigger Width') plt.xlabel('Outrigger Width (m)') plt.ylabel('Maximum Roll Angle (degrees)') plt.grid(True) plt.show() # 결과 출력 for width, max_angle in zip(outrigger_widths, max_angles): print(f"Outrigger Width: {width}m, Max Roll Angle: {max_angle:.2f} degrees")인공지능 정말 똑똑하네요.
인공지능은 아직 개발 초기단계라는거...


세상의모든계산기 님의 최근 댓글
고장남 - POST 진입 실패, 모니터 안나옴 직접 사용할 일이 없어져서, 고향집에 가져다 놓고 어댑터만 꼽아 두었습니다. 마지막으로 켠 것은 25년 6월쯤이 아니었을까 싶습니다. (이상증상은 없었구요) 이번 추석에 가서 켜 보니까, 화면이 아예 안나오더라구요. 집에 가져와서 분해해 살펴보니까 - 어댑터 12V는 정상 - 어댑터 꼽으면 바로 POWER 는 켜집니다. ㄴ POWER ON -> Fan 돌아감 + 파워 LED 들어옴 + NVME에 LED 들어옴 ㄴ HDMI 1, 2 신호 전혀 안들어옴 (모니터 2대 확인) ㄴ 키보드에 LED 안들어옴 (USB 5V 가 안들어오는 듯 함) - 옆구리 버튼은 작동하지 않습니다. 길게 눌러도 꺼지지 않음. 하나씩 제거하면서 변수를 제거해 봤는데, 뭘 해도 상태가 똑같습니다. 보드쪽에 문제가 생긴 것 같습니다. 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14 낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10