ESB 서체 - EBS 훈민정음 / EBS 훈민정음 새론체 / EBS 주시경
사이트 방문해서 다운받으실 수 있습니다.
https://about.ebs.co.kr/kor/organization/font?tabVal=hunmin
소개
교육 한류와 올바른 언어사용을 선도하고 있는 EBS가 훈민정음 반포 568돌 기념 한글날을 맞아 새롭게 개발한 “EBS 훈민정음”을 전 국민대상으로 무료 배포합니다.
EBS가 제작하여 무료 배포하는 “EBS 훈민정음”은 훈민정음 창제와 더불어 목판으로 제작된 해례본체의 기본형과 주요특징을 유지하면서 단순화한 획과 선으로 디자인하여 글꼴의 가독성을 높이고 데이터를 줄여 모바일과 웹 환경에 최적화하였습니다.
글꼴 및 다운로드

글꼴 모듈 및 기본틀 구성
- EBS 훈민정음 글꼴 모듈
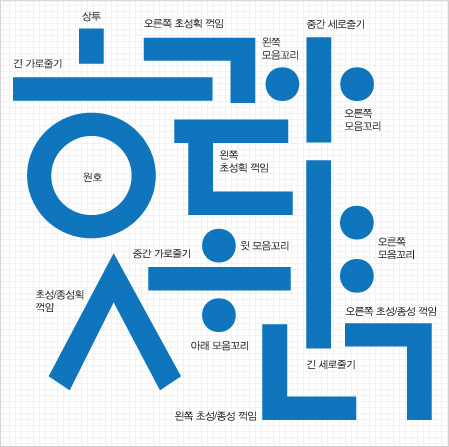
- EBS 훈민정음 기본틀 구성
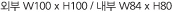
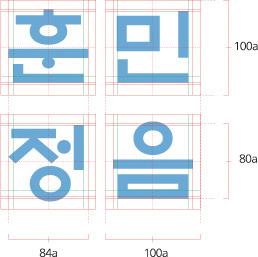
자음 및 모음구성
- EBS 훈민정음 자음구성

- EBS 훈민정음 모음구성

사용안내
- 1. 저작권
- EBS 훈민정음의 저작권 및 소유권의 제반권리는 EBS한국교육방송공사에 있습니다.
- 2. 사용범위
- 가. 학교, 개인, 공공기관 등 누구나 무료로 다운로드하여 사용할 수 있습니다.
- 나. 영상매체, 인쇄매체, 웹, 모바일 등 매체와 용도에 제한 없이 상업적으로도 사용이 가능합니다.
- 3. 제한사항
- 가. EBS의 사전 서면승인 없이 <EBS훈민정음 새론체>의 소스코드 수정 및 역설계 등 일부 혹은 전부를 임의로 변형할 수 없습니다.
- 나. EBS의 사전 서면승인 없이 서체자체의 임의개작, 개명을 통한 재배포나 재판매 등의 행위는 금지됩니다.
- 다. 음란물, 반사회적 제작물 등 부정적 이미지의 제작물에 사용할 수 없습니다.



세상의모든계산기 님의 최근 댓글
예시11) 선형 연립방정식에서 답이 false 로 나올 때 https://allcalc.org/55823 2025 10.22 approx(참 해) 값이 이상하게 튀는 것 같아서 AI를 이용해 (python 으로) 구해보았습니다. * python 의 유효자릿수가 nspire 의 유효자릿수(14자리~15자리)보다 더 길기 때문에 시도하였습니다. ** 원래는 wolfram alpha 로 구해보려고 했는데, 울프람에서는 수식 길이가 너무 길다고 거부하는 바람에 포기하였습니다. 그 결과, AI approx(참 해) 값은 정상 범주에 포함되었고, 이는 solve()로 구한 대부분의 결과값과 유사하였습니다. 그럼 nspire 의 approx(참 해)는 왜 튀었나? 참 해에 더하기,빼기,곱하기,나누기 가 너무 많이 포함되어 있다보니, 모두 계산하고 나면 오차가 누적&증폭되어 버리는 것 같습니다. 그래서 오히려 solve의 numeric 한 접근보다도 더 큰 오차가 발생한 듯 하고, 그래서 적절한 해의 x 구간을 벗어나버린 듯 합니다. 그것이 처음의 solve 에서 false 를 이끌어낸 주 원인이 아니었을까요? (추정) 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 참 값을 approx() 로 변환한 근사값은 원래 방정식 모두를 만족할 수 없지만, linsolve() 로 찾은 근사값과, AI로 참 값을 근사변환한 값은 원래 방정식 모두를 만족할 수 있습니다. 2025 10.21