- 세상의 모든 계산기 자유(질문) 게시판 질문 ()
TI NSPIRE CX CAS에서 행렬의 곱으로 분해하는 방법을 좀 알려주세요.
안녕하세요.
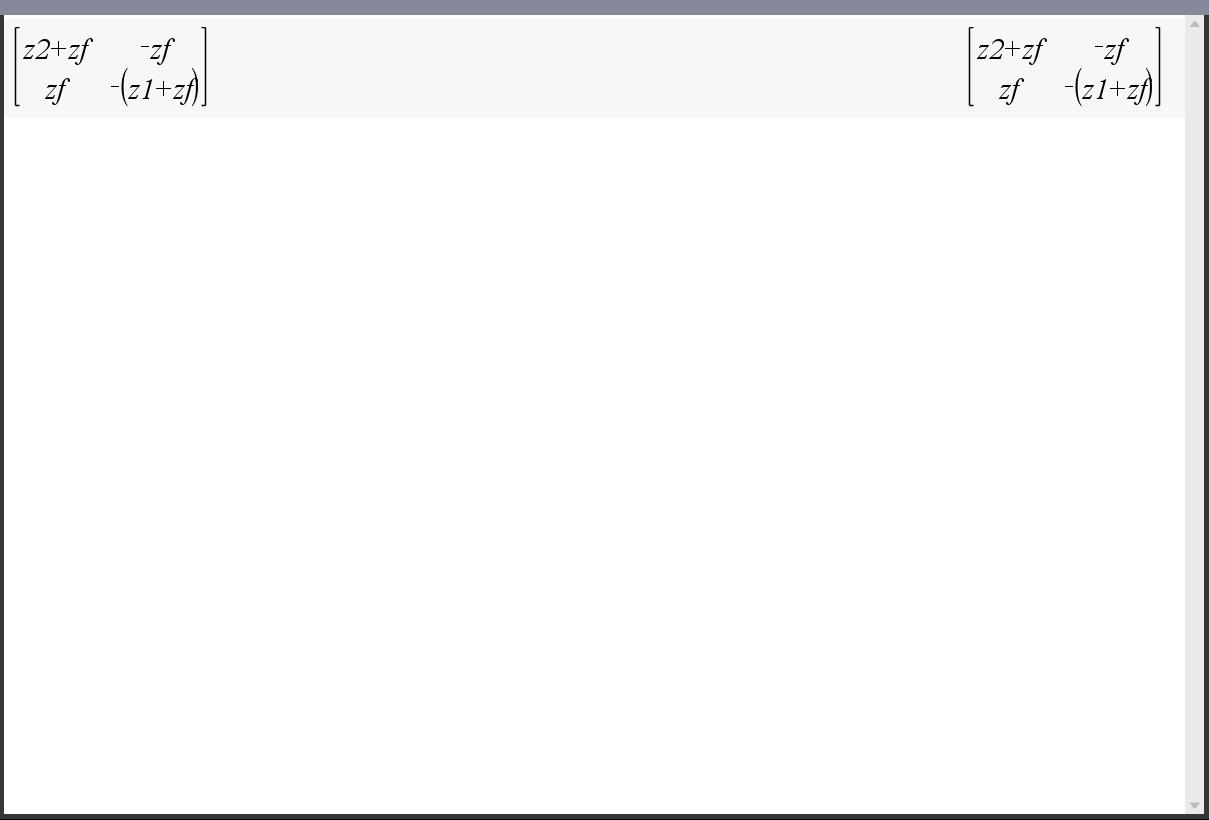
보기와 같은 2*2 행렬이 z1, z2, zf 3개의 인자로 구성이 되어 있습니다.
2*2 행렬을 행렬의 곱으로 표현을 하려고 합니다.
(2*3 행렬) 곱하기 (3*2 행렬)로 만들면 가능할 거 같은데요.
아무리 생각을 해 봐도 행렬의 곱으로 표현을 할 수 있는지 생각이 나지를 않네요.
polycoeffs 명령어를 적절히 하면 될거 같은데 잘 모르겠네요.
도움 좀 부탁 드리겠습니다.
늘 감사합니다.
댓글7
-
세상의모든계산기2024.06.20 - 16:33 #41911
TI-nspire 에 내장된 기능중에 행렬을 분해하는 기능은
LU Decomposition 이 유일한 것으로 보입니다.
[TI-nspire] 행렬 LU 분해 = LU Decomposition = LU fatorization

그 외의 방법으로 분해를 하는 것은 불가능하며,
원하시는 구조가 있다면 그에 맞게 프로그램을 작성하시는 방법 뿐입니다.
-
세상의모든계산기
ChatGPT-4o 에게 물어보니 이렇게 답해주네요.
주어진 행렬을 다음과 같이 정의합니다:
\[ \begin{pmatrix}z_2 + z_f & -z_f \\ z_f & -(z_1 + z_f) \end{pmatrix} \]
이제 이 행렬을 두 개의 행렬의 곱으로 분해하는 방법을 살펴보겠습니다.
### 방법 1: 두 개의 \(2 \times 2\) 행렬로 분해
분해하고자 하는 행렬 \(A\)를 두 개의 \(2 \times 2\) 행렬 \(B\)와 \(C\)의 곱으로 표현할 수 있습니다:
\[ A = B \cdot C \]
행렬 \(B\)와 \(C\)를 다음과 같은 형태로 두어 보겠습니다:
\[ B = \begin{pmatrix} a & b \\ c & d \end{pmatrix}, \quad C = \begin{pmatrix} e & f \\ g & h \end{pmatrix} \]
그러면, \(B \cdot C\)는 다음과 같이 계산됩니다:
\[ B \cdot C = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} e & f \\ g & h \end{pmatrix} = \begin{pmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{pmatrix} \]
이제 이 결과를 원래의 행렬 \(A\)와 비교하여 각 성분이 일치하도록 식을 세워봅시다:
\[ \begin{pmatrix} ae + bg & af + bh \\ ce + dg & cf + dh \end{pmatrix} = \begin{pmatrix} z_2 + z_f & -z_f \\ z_f & -(z_1 + z_f) \end{pmatrix} \]
이를 통해 다음과 같은 네 개의 방정식을 얻습니다:
1. \( ae + bg = z_2 + z_f \)
2. \( af + bh = -z_f \)
3. \( ce + dg = z_f \)
4. \( cf + dh = -(z_1 + z_f) \)
이 네 개의 방정식을 만족하는 \(a, b, c, d, e, f, g, h\)를 찾으면 됩니다.
### 방법 2: \(2 \times 3\)와 \(3 \times 2\) 행렬로 분해
행렬 \(A\)를 \(2 \times 3\) 행렬 \(P\)와 \(3 \times 2\) 행렬 \(Q\)의 곱으로 분해해보겠습니다:
\[ A = P \cdot Q \] 행렬 \(P\)와 \(Q\)를 다음과 같이 정의합니다:
\[ P = \begin{pmatrix} a & b & c \\ d & e & f \end{pmatrix}, \quad Q = \begin{pmatrix} g & h \\ i & j \\ k & l \end{pmatrix} \]
그러면 \(P \cdot Q\)는 다음과 같이 계산됩니다:
\[ P \cdot Q = \begin{pmatrix} a & b & c \\ d & e & f \end{pmatrix} \begin{pmatrix} g & h \\ i & j \\ k & l \end{pmatrix} = \begin{pmatrix} ag + bi + ck & ah + bj + cl \\ dg + ei + fk & dh + ej + fl \end{pmatrix} \]
이제 이 결과를 원래의 행렬 \(A\)와 비교하여 각 성분이 일치하도록 식을 세워봅시다:
\[ \begin{pmatrix} ag + bi + ck & ah + bj + cl \\ dg + ei + fk & dh + ej + fl \end{pmatrix} = \begin{pmatrix} z_2 + z_f & -z_f \\ z_f & -(z_1 + z_f) \end{pmatrix} \]
이를 통해 다음과 같은 네 개의 방정식을 얻습니다:
1. \( ag + bi + ck = z_2 + z_f \)
2. \( ah + bj + cl = -z_f \)
3. \( dg + ei + fk = z_f \)
4. \( dh + ej + fl = -(z_1 + z_f) \)
이 네 개의 방정식을 만족하는 \(a, b, c, d, e, f, g, h, i, j, k, l\)를 찾으면 됩니다.
이와 같은 식을 풀기 위해서는 다양한 방법을 사용할 수 있습니다.
예를 들어, 특정 값을 대입하거나, 행렬의 고유값 분해를 이용할 수도 있습니다.
그러나 주어진 조건이 복잡할 경우, 수치 해석적 방법을 사용할 수도 있습니다.
-
세상의모든계산기
그런 일반론적인 방법 말고, 무슨 알고리즘에 의한 방법은 없을까? 예를 들자면 LU 분해라거나
주어진 행렬을 분해하기 위해 LU 분해와 같은 알고리즘적인 접근 방법을 고려할 수 있습니다. LU 분해는 일반적으로 정사각 행렬을 하삼각행렬(L)과 상삼각행렬(U)로 분해하는 방법입니다. 그러나 주어진 행렬을 두 개의 2×2 행렬의 곱으로 분해하는 문제를 해결하기 위해, LU 분해나 다른 구체적인 알고리즘을 적용하는 방법에 대해 설명드리겠습니다.
LU 분해
LU 분해는 행렬을 하삼각행렬 L과 상삼각행렬 U로 분해하는 알고리즘입니다. 하지만 주어진 행렬을 두 개의 일반적인 2×2 행렬로 분해하기 위해서는 LU 분해 외에도 다른 방법을 고려해야 할 수 있습니다. 그러나 일단 LU 분해를 사용하여 문제를 풀어보겠습니다.
행렬 A를 다음과 같이 정의합니다:
\[ \begin{pmatrix} z_2 + z_f & -z_f \\
z_f & -(z_1 + z_f)
\end{pmatrix} \]
이 행렬을 LU 분해하면 다음과 같은 형태가 됩니다:
\[ A = LU \]
여기서 \(L\)은 하삼각행렬이고 \(U\)는 상삼각행렬입니다.
행렬 \(L\)과 \(U\)의 형태는 다음과 같습니다:
\[ L = \begin{pmatrix}
1 & 0 \\
l_{21} & 1
\end{pmatrix}, \quad U = \begin{pmatrix}
u_{11} & u_{12} \\
0 & u_{22}
\end{pmatrix} \]
이제 \(LU\)의 곱을 계산하여 원래 행렬 \(A\)와 같게 만들어 보겠습니다:
\[ \begin{pmatrix}
1 & 0 \\
l_{21} & 1
\end{pmatrix} \begin{pmatrix}
u_{11} & u_{12} \\
0 & u_{22}
\end{pmatrix} = \begin{pmatrix}
u_{11} & u_{12} \\
l_{21}u_{11} & l_{21}u_{12} + u_{22}
\end{pmatrix} \]
이를 행렬 \(A\)와 비교하여 성분별로 일치시키면 다음과 같은 방정식을 얻습니다:
1. \( u_{11} = z_2 + z_f \)
2. \( u_{12} = -z_f \)
3. \( l_{21}u_{11} = z_f \)
4. \( l_{21}u_{12} + u_{22} = -(z_1 + z_f) \)
이제 각 방정식을 풀어 보겠습니다:
1. \( u_{11} = z_2 + z_f \)
2. \( u_{12} = -z_f \)
3. \( l_{21}(z_2 + z_f) = z_f \) 에서 \( l_{21} = \frac{z_f}{z_2 + z_f} \)
4. \( \frac{z_f}{z_2 + z_f}(-z_f) + u_{22} = -(z_1 + z_f) \)
따라서 \( u_{22} \)는 다음과 같이 구할 수 있습니다:
\[ u_{22} = -(z_1 + z_f) + \frac{z_f^2}{z_2 + z_f} \]
\[ u_{22} = \frac{-(z_1 + z_f)(z_2 + z_f) + z_f^2}{z_2 + z_f} \]
\[ u_{22} = \frac{-z_1z_2 - z_1z_f - z_fz_2 - z_f^2 + z_f^2}{z_2 + z_f} \]
\[ u_{22} = \frac{-z_1z_2 - z_1z_f - z_fz_2}{z_2 + z_f} \]
따라서 \(L\)과 \(U\)는 다음과 같습니다:
\[ L = \begin{pmatrix}
1 & 0 \\
\frac{z_f}{z_2 + z_f} & 1
\end{pmatrix}, \quad U = \begin{pmatrix}
z_2 + z_f & -z_f \\
0 & \frac{-z_1z_2 - z_1z_f - z_fz_2}{z_2 + z_f}
\end{pmatrix} \]
### 다른 행렬 분해 알고리즘
주어진 행렬을 \(2 \times 3\) 행렬 \(P\)와 \(3 \times 2\) 행렬 \(Q\)로 분해하는 다른 방법으로 SVD (Singular Value Decomposition) 또는 QR 분해를 사용할 수 있습니다.### SVD (Singular Value Decomposition)
행렬 \(A\)는 다음과 같이 세 행렬의 곱으로 분해할 수 있습니다:
\[ A = U \Sigma V^T \]
여기서 \(U\)는 직교 행렬, \(\Sigma\)는 대각 행렬, \(V\)는 직교 행렬입니다. 이 방법을 통해 \(A\)를 \(2 \times 3\) 행렬과 \(3 \times 2\) 행렬로 분해할 수 있습니다.
구체적인 알고리즘 적용은 수학적 계산을 통해 정확한 값을 도출해야 하지만, 이러한 기본적인 알고리즘적 접근을 통해 원하는 분해를 수행할 수 있습니다. SVD의 경우, 수치적 계산이 필요하므로 소프트웨어 도구를 사용하는 것이 일반적입니다.
이와 같은 알고리즘적인 방법을 사용하면 주어진 행렬을 다양한 형태로 분해할 수 있습니다.


조니 님의 최근 댓글
예전에 질문을 했었던 이슈네요. 잊어버리고 있다가 다시금 알게 되었습니다. 감사합니다. 2025 09.29 짝수승을 대입을 하면 극한값이 계산이 되네요. 덕분에 오늘도 또 한개 배우고 갑니다. 2025 08.06 역시 저의 실수였군요. 늘 감사드립니다. 2025 08.01 그렇군요. 알려주셔서 감사합니다. 2025 06.05 안되는 거였군요. 오늘도 또 하나 배우고 갑니다. 2025 05.21