- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
인공지능(AI) 수학능력 TEST
앞의 글에서 조니님께서 질문하신 것을 인공지능에게 물어봤습니다.
과연 답변을 잘 할까요?
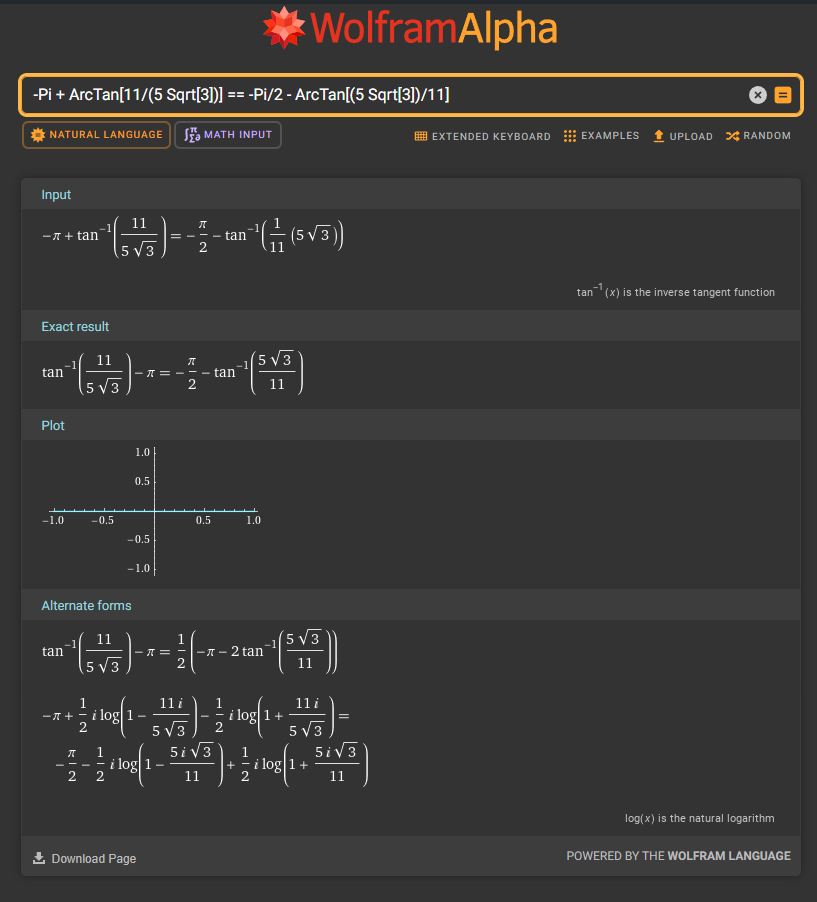
일단 울프람알파는 명확하게 답변을 안하네요.
댓글9
-
세상의모든계산기2024.05.21 - 10:41 #40794
ChatGPT-4o 에게 물어 봤습니다.
To determine if the equation
is true or false, we can simplify and compare both sides.
### Left Side:
### Right Side:
### Using the Identity for $\arctan$:
We use the identity for the sum of arctangents:
This identity holds when .
In this case, let and :Since , the sum formula becomes:
Thus,
Now, substitute this back into the original equation:
### Left Side Simplification:
### Comparing Left and Right Sides:
The simplified left side is:
This matches the right side exactly. Therefore, the original equation is:
Thus, the statement is **true**.
-
조니
저도 chatgpt-4인데 false가 나오네요. 이 것도 부호 계산을 틀리게 하네요. ㅠㅠ
-
조니
chatgpt 3.5는 true가 나오는게 approximate를 사용해서 같다고 결론을 도출하는데, 이건 아닌거 같습니다. ㅎㅎ
그리고 한글 버전에서는 계산이 안되는데 영문 버전에서는 그나마 엉터리 같지만 결과가 근사하게 나오기는 하네요.
-
-
세상의모든계산기2024.05.21 - 10:44 #40799
제미나이에게도 같은 질문으로 물어 봤습니다.
The statement "-Pi + ArcTan[11/(5 Sqrt[3])] == -Pi/2 - ArcTan[(5 Sqrt[3])/11]" is false.
To prove this, we can simplify both sides of the equation:
Left side:
-Pi + ArcTan[11/(5 Sqrt[3])]
= -Pi + ArcTan[11/(5 * 3^(1/2))]
= -Pi + ArcTan[11/(5 * (3^1/2))]
= -Pi + ArcTan[(11 * 3^(-1/2)) / 5]
= -Pi + ArcTan[(11 * (1/3^(1/2))) / 5]
= -Pi + ArcTan[(11/3^(1/2)) / 5]
Right side:
-Pi/2 - ArcTan[(5 Sqrt[3])/11]
= -Pi/2 - ArcTan[(5 * 3^(1/2)) / 11]
= -Pi/2 - ArcTan[(5 * (3^1/2)) / 11]
= -Pi/2 - ArcTan[(5/11) * (3^1/2)]
= -Pi/2 - ArcTan[(5/11) * (1/3^(1/2))]
= -Pi/2 - ArcTan[(5/(11 * 3^(1/2)))]
= -Pi/2 - ArcTan[(5/(11 * (1/3^(1/2)))]
= -Pi/2 - ArcTan[(5/(11/3^(1/2)))]
= -Pi/2 - ArcTan[(5 * 3^(1/2)) / 11]
Comparing the simplified forms of both sides, we see that they are not equal. Therefore, the original statement is false.
Additional verification:
We can also use a graphing calculator to verify that the two expressions do not have the same value. Plotting both expressions on a graph, we can see that they have different y-intercepts and slopes. This confirms that the two expressions are not equal.
Conclusion:
Based on the above analysis, we can conclude that the statement "-Pi + ArcTan[11/(5 Sqrt[3])] == -Pi/2 - ArcTan[(5 Sqrt[3])/11]" is false.
-
조니
제미나이 저도 해 봤는데 true라고 나오네요
그런데 이건 좀 희한한게 tan(pi/6)을 -루트3/3으로 부호를 틀리게 계산을 했는데도 결과가 맞다고 도출하는게 올바른 결과인지 의문입니다.
-
세상의모든계산기
Copilot 에게도 물어 봤습니다.
True! The given equation holds. Both sides are equal. Here’s the breakdown:1. Start with the left-hand side (LHS):
2. Simplify the fraction:
3. Use the identity:
Applying this to our expression:
4. Simplify the second term:
5. Combine the arctan terms:
6. Use the identity again:
Applying this to our expression:
7. Simplify the numerator:
And the denominator:
8. Final result:
Since
, we have:
Therefore, the LHS equals
.
9. Now let’s look at the right-hand side (RHS):
10. We already found that
So the RHS also equals
.
Since both sides are equal, the given equation is true! �




세상의모든계산기 님의 최근 댓글
참고 https://allcalc.org/52065 TI NSPIRE CX CAS 복소수 관련 문제 문의 드립니다. 2025 09.28 Rectangular 설정시 ▶Polar 2025 09.28 Real or Cpmplex Format : Polar 설정시 2025 09.28 비교 AC-68U[ ID] Interval Transfer Bandwidth[ 4] 0.00-10.00 sec 475 MBytes 398 Mbits/sec sender[ 4] 0.00-10.00 sec 475 MBytes 398 Mbits/sec receiver 2025 09.24 비교 : AC-68U [ ID] Interval Transfer Bandwidth [ 4] 0.00-10.01 sec 65.0 MBytes 54.5 Mbits/sec sender [ 4] 0.00-10.01 sec 65.0 MBytes 54.5 Mbits/sec receiver 이상해서 다시 접속 C:\iperf-3.1.3-win64>iperf3.exe -c 192.168.68.36 -p 5000 -t 10 -f m -i 2 Connecting to host 192.168.68.36, port 5000 [ 4] local 192.168.68.217 port 12792 connected to 192.168.68.36 port 5000 [ ID] Interval Transfer Bandwidth [ 4] 0.00-2.00 sec 22.4 MBytes 93.7 Mbits/sec [ 4] 2.00-4.00 sec 24.5 MBytes 103 Mbits/sec [ 4] 4.00-6.00 sec 23.6 MBytes 98.9 Mbits/sec [ 4] 6.00-8.01 sec 24.2 MBytes 101 Mbits/sec [ 4] 8.01-10.00 sec 24.1 MBytes 102 Mbits/sec - - - - - - - - - - - - - - - - - - - - - - - - - [ ID] Interval Transfer Bandwidth [ 4] 0.00-10.00 sec 119 MBytes 99.7 Mbits/sec sender [ 4] 0.00-10.00 sec 119 MBytes 99.7 Mbits/sec receiver * 공유기 2.4G 연결된 장치가 많아서 연결속도/다운속도가 떨어지는 것이 아닌가 합니다. 2025 09.24