- 세상의 모든 계산기 자유(질문) 게시판 리뷰 ()
[벤치마크] SSD, Kingston A400 120GB CrystalDiskMark 비교 (feat. Sandisk X110)
-
- 2019.08.18 - 14:22 2018.09.09 - 21:34 1365 4
최근(한달 조금 넘었나?) (내돈주고) 구입한 킹스턴 A400 (120GB) 제품의 벤치마크 결과입니다.
샌디스크 X110은 UpgradeBAY(ODD Bay)에 꼽혀 있고, A400은 HDD Bay에 꼽혀 있습니다만... 그건 별 영향이 없을 듯 싶구요.
전반적으로 엎치락 뒷치락 하는데 4KiB Q8T8 Read 는 차이가 많이 나는군요. (322.1MB/s vs 112.7MB/s)
체감상 차이는 없을 듯 합니다.
* 벤치마크한 시스템
HP 8460p, SATA2 연결, HDD BAY(킹스턴 A400, 포맷 직후), ODD BAY(X110, OS, 부팅)
-
25
댓글4
-
세상의모든계산기
it동아의 벤치마크 결과 http://it.donga.com/27228/
(버전업에 따른 측정항목의 차이는 그렇다고 치더라도)
결과에 유의미한 차이가 있는 것 같아서 구버전을 다운받아서 돌려봤습니다.
<벤치마크 1차>
이거 OS 마이그레이션 설치하고 사소한 문제생겨서 PC초기화(개인설정 남김)한 직후인데,
그 때문인건지 결과가 엉망이네요. 나중에 다시 해봐야 할 듯.
<벤치마크 2차>
PC 초기화(개인설정 삭제)한 직후에 다시 벤치 돌렸습니다. 결과는 1차와 동일합니다.
현재 시스템이 뭔가 꼬인 모양입니다. HDD하고 충돌나는 것 같기도 하구요.
<벤치 3차>
하드웨어 구성은 1차 2차와 동일한 상태에서, HDD로 부팅해서 테스트 해봤습니다.
4K Q32T1 결과가 불스럽지만, 그래도 쓰기 성능이 어느 정도 정상화되었습니다.OS 설치/부팅한 상태에서 벤치가 제대로 되지 않는 것인지...
<4차 벤치마크>C: 의 페이지 파일을 없애고 > 재부팅하고 > 다시 벤치
좀 나아졌다고 해야할지... -
세상의모든계산기
1년쯤 사용하였고,
주 사용 디스크 상태로 측정해 보았느데... ㅎㄷㄷ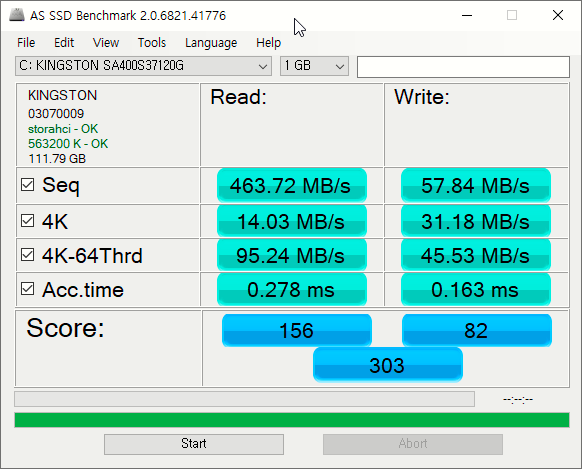
Seq Write 58 MB/s 이거 뭡니까!
-
세상의모든계산기
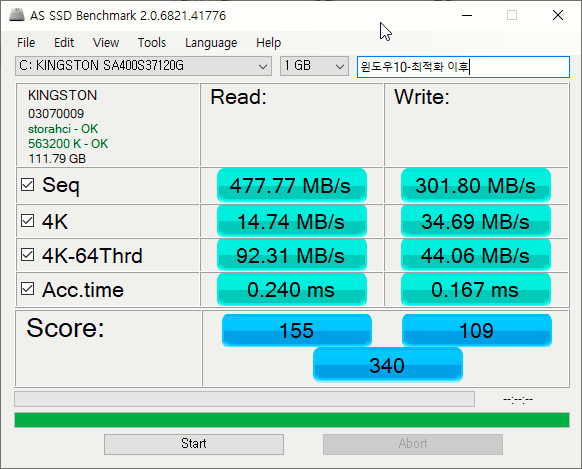
윈도우 디스크 속성 - 도구 - 드라이브 최적화 이후에 좋아졌습니다.
세상의모든계산기 님의 최근 댓글
예시11) 선형 연립방정식에서 답이 false 로 나올 때 https://allcalc.org/55823 2025 10.22 approx(참 해) 값이 이상하게 튀는 것 같아서 AI를 이용해 (python 으로) 구해보았습니다. * python 의 유효자릿수가 nspire 의 유효자릿수(14자리~15자리)보다 더 길기 때문에 시도하였습니다. ** 원래는 wolfram alpha 로 구해보려고 했는데, 울프람에서는 수식 길이가 너무 길다고 거부하는 바람에 포기하였습니다. 그 결과, AI approx(참 해) 값은 정상 범주에 포함되었고, 이는 solve()로 구한 대부분의 결과값과 유사하였습니다. 그럼 nspire 의 approx(참 해)는 왜 튀었나? 참 해에 더하기,빼기,곱하기,나누기 가 너무 많이 포함되어 있다보니, 모두 계산하고 나면 오차가 누적&증폭되어 버리는 것 같습니다. 그래서 오히려 solve의 numeric 한 접근보다도 더 큰 오차가 발생한 듯 하고, 그래서 적절한 해의 x 구간을 벗어나버린 듯 합니다. 그것이 처음의 solve 에서 false 를 이끌어낸 주 원인이 아니었을까요? (추정) 2025 10.21 그래프로 확인 그래프 함수로 지정하고, 매우 좁은 구간으로 그래프를 확대해 보면 불연속적인 그래프 모습이 확인됩니다. 이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문일 것이구요. 다만 특이한 점은, 그래프상으로 교점에 해당하는 구간이 73.049507058477≤x≤73.049507058484 사이로 나오는데 -> 이 구간은 'solve에서 여러 방법으로 직접 구해진 해들'은 포함되는 구간입니다. -> 하지만, '참값인 해를 계산기로 구한 appprox 값 x=73.049507058547'은 포함되지 않는 구간입니다. 2025 10.21 tns 파일 첨부 sol_num_vs_exact.tns 2025 10.21 검증하면 1번 식을 x에 대해 정리하고, → 그 x 값을 2번 식에 대입해 넣으면 → 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음. 얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음. 구해진 참값의 근사값을 구하면 x=73.049507058547 and y=23.747548955927 참 값을 approx() 로 변환한 근사값은 원래 방정식 모두를 만족할 수 없지만, linsolve() 로 찾은 근사값과, AI로 참 값을 근사변환한 값은 원래 방정식 모두를 만족할 수 있습니다. 2025 10.21