- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
알파고 ELO Rating 이 4500??
-
- 2024.03.17 - 19:45 2016.03.27 - 13:12 2015 6
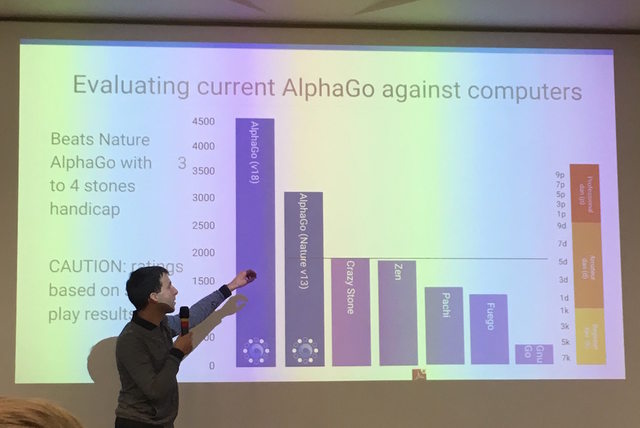
사진 출처 :
http://test.pgr21.com/pb/pb.php?id=humor&no=269200
http://gall.dcinside.com/board/view/?id=baduk&no=137040&page=5
http://www.lifein19x19.com/forum/viewtopic.php?f=18&t=12922
https://www.zhihu.com/question/41780229
David Silver yesterday gave a lecture at UCL, which refers to the ELO ratings AlphaGo, where chess with Shishi version (v18) actually has up to 4500 points, allowing the arm with Fan chess that paragraph AlphaGo (v13) four sub . ELO rating is the score http://goratings.org on the current world chess Ke Jie was the first person to 3615 points - the points difference Elo rating represents the corresponding winning percentage, 800 points, then the difference between winning percentage is 100%, the difference between 677 if winning is 99%. Shishi learned this after watching scores of the fourth set, with no set up (?) Cherish the AlphaGo labeled bug state, is really not easy.
중국어 -> 영어 구글 번역
- Nature v13 = 판후이와 대국했던 시절(네이쳐 논문발표) 버전의 알파고
- v18 = 이세돌과 대국한 버전의 알파고 (하드웨어 동일?)
- v18 의 기력 측정은 Nature v13 과 4점 접바둑을 통해 측정한 기력
-
25
댓글6
-
세상의모든계산기
출처 : http://www.bbsdigest.com/thread/index?bid=87&tid=31270999
I'm a PhD student in Computational Neuroscience/Machine Learning who attended a talk today at UCL by David Silver, lead author on the AlphaGo Nature paper: http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html Although unfortunately I didn't take any pictures, I can confirm he did show us some slides on AlphaGo's evaluation functions and how their assessment of the probability of winning changed during the course of each match.
Since I heard there was some interest about whether the game is balanced in its initial state, I looked carefully at the initial intersection with the y-axis, corresponding to the point at which no moves had been played. I can confirm that according to the Value Network's assessment, white has an initial probability of winning bigger that 50%, my guess being 53% (the scale used a 25% interval and so was very hard to read). By contrast, the Monte Carlo rollout had what looked like an almost exact 50-50 assessment. Although AlphaGo uses both assessments, David Silver said that the Value Network is in general more accurate and is thus more highly weighted in the latest versions of AlphaGo. So it's fair to say AlphaGo thinks white (with 7.5 komi) has a small advantage.
Also, one other interesting tidbit is that according to Deepmind's internal assessment, AlphaGo's ELO was much, much bigger than Lee Sedol's (above 4000 iirc). However, David Silver acknowledged that he didn't really trust their internal assessment as AlphaGo was only playing versions of itself by reinforcement learning, and so may have been completely unaware of surprising strategies which can beat it. Which is why they had to play Lee Sedol in those exciting matches (and indeed, according to their internal ELO they probably would have expected 5-0 not 4-1)
Hope you find this interesting anyway, I sure did!요약
- 알파고 가치망에서는 덤7.5집일 때 백이 약간이나마 유리하다고 평가
- 알파고 ELO 4500 은 간접측정이라 신뢰성이 부족.
-
세상의모든계산기
구글 번역 사이트가 인공신경 지능망으로 업그레이드 되었다고 합니다. (2016-11-16)
그래서 위의 영문을 번역시켜 보았습니다.저는 Computational Neuroscience / Machine Learning의 박사 과정 학생으로서 AlphaGo Nature 논문의 수석 저자 David Silver가 UCL에서 오늘 연설을했습니다 : http://www.nature.com/nature/journal/v529/n7587/full /nature16961.html 불행히도 사진을 찍지는 않았지만 AlphaGo의 평가 기능에 대한 슬라이드와 각 경기가 진행되는 동안 우승 확률에 대한 평가가 어떻게 달라지는 지 확인할 수있었습니다.
게임이 초기 상태에서 균형을 이루는 지에 대한 관심이 있다고 들었으므로 움직이지 않는 지점에 해당하는 y 축과의 초기 교차점을주의 깊게 살펴 봤습니다. Value Network의 평가에 따르면 흰색은 초기 확률이 50 % 이상인 것으로 나타났습니다. 내 생각에 53 % (25 %의 눈금을 사용했기 때문에 읽는 것이 매우 어려웠습니다)입니다. 대조적으로, 몬테카를로 롤아웃은 거의 정확한 50-50 평가처럼 보였습니다. AlphaGo는 두 가지 평가를 모두 사용하지만 David Silver는 Value Network가 일반적으로 정확하고 AlphaGo의 최신 버전에 더 가중되어 있다고 말했습니다. 그래서 AlphaGo는 흰색 (7.5 komi)이 작은 이점을 가지고 있다고 생각한다고 말하는 것은 공평합니다.
또한, 흥미로운 또 하나의 재미있는 점은 Deepmind의 내부 평가에 따르면 AlphaGo의 ELO가 Lee Sedol (4000 iirc 이상)보다 훨씬 크다는 것입니다. 그러나 David Silver는 AlphaGo가 강화 학습을 통해 버전을 재생하기 때문에 내부 평가를 실제로 신뢰하지 않았기 때문에이를 극복 할 수있는 놀라운 전략을 전혀 알지 못했을 수도 있음을 인정했습니다. 그래서 그들이 흥미 진진한 경기에서 Lee Sedol과 경기를해야했던 이유입니다. (실제로 내부 ELO에 따르면 그들은 아마도 5-0에서 4-1로 예상했을 것입니다)
어쨌든이 재미있는 것을 찾으시기 바랍니다.와우... 인상적이네요.
-
세상의모든계산기
참고 : 한국기원 기사 랭킹제도
https://www.baduk.or.kr/record/ranking_info.asp- 승률 기대치 = E(d) =
- 조정되는 점수 =
K=16,
α=0.8=패자에게만 주어지는 위로점수? (디플레이션 방지 목적)
* 가중치
예선 본선 결승전(도전기) 1등급 기전 1.5 2.3 3.0 2등급 기전 1.3 1.9 2.5 3등급 기전 1.0 1.5 2.0 제한 기전 및 특별 대국 1.0 1.0 1.5 * 임시점수 : 대국 숫자가 적은 선수는 임시점수제도를 통해 점수 부여
-
세상의모든계산기
절예 // 가중치 개선 진행중?
카타고 (18*384nbt) // 가중치 개선 진행중
카타고 (60*320)
카타고 (40*384)
카타고 (40*256)
카타고 (30*256)
카타고 (20*256)
알파고 제로 (40*256, 40일)
릴라 제로 #272 (40*256)
미니고 v17 (20*256)
미니고 v16 (40*256)
알파 제로 (20*256, 36시간)
엘프고 v2 (20*256)
알파고 제로 (20b, 3일)
알파고 마스터
인간 프로 기사 GOAT
알파고 리 (=인간 프로 기사 최상급)
인간 프로 기사 현역
알파고 판
기준 : 블럭*채널, 가장 강한 가중치 버전
직접 대국하지 않은 것이 많아 추정일 뿐임.
https://www.reddit.com/r/baduk/comments/hma3nx/unified_elo_rating_for_ais/
위 글을 기본으로 작성한 순위표임. / SHKD13 작성https://github.com/breakwa11/GoAIRatings#go-ai-ratings
기본적으로는 여기서 많이 가져온 듯 하고,
알파고와 비교할 수 있는 것은 엘프고 개발자의 멘트가 중요했던 듯 싶음.
세상의모든계산기 님의 최근 댓글
수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17 Gemini-2.5-pro 답변 ✦ 현대 컴퓨터 대수 시스템(CAS) 계산기에 탑재된 solve 기능의 일반적인 내부 동작 원리에 대해 설명해 드리겠습니다. 현대 CAS의 solve 기능은 단순히 하나의 알고리즘으로 작동하는 것이 아니라, 마치 '순수 수학자'와 '문제 해결 공학자'가 협력하는 것처럼, 여러 단계에 걸친 정교한 '하이브리드(Hybrid)' 방식으로 동작합니다. solve 함수의 작동 과정 1단계: 기호적 해법 (Symbolic Solver) - '순수 수학자'의 접근 계산기는 가장 먼저 방정식을 대수적으로, 즉 정확한 수학적 해를 찾으려고 시도합니다. 이 단계는 마치 사람이 공식을 이용해 문제를 푸는 과정과 같습니다. 1. 방정식 분석: solve 명령을 받으면, 시스템은 먼저 입력된 방정식의 구조를 분석합니다. (예: 이것이 다항식인가? 삼각방정식인가? 로그방정식인가?) 2. 규칙 기반 풀이: 분석된 구조에 따라, 시스템은 내장된 방대한 수학 규칙 라이브러리를 적용합니다. * 선형/이차 방정식: ax+b=c 나 ax²+bx+c=0 같은 형태는 이항, 인수분해, 근의 공식 등을 이용해 즉시 풉니다. * 고차 다항식: 인수분해, 조립제법 등의 규칙을 적용하여 유리수 해를 찾습니다. * 삼각방정식: sin(x) = 0.5 와 같은 경우, x = nπ + (-1)ⁿ * (π/6) 와 같이 주기성을 고려한 일반해 공식을 적용합니다. * 기타: 로그, 지수 법칙 등 해당 방정식에 맞는 대수적 풀이법을 총동원합니다. 3. 결과: 이 단계에서 해를 찾으면, 1.414... 와 같은 근사값이 아닌 √2 나 π/3 와 같은 정확한 기호 형태의 해를 반환합니다. > 강점: 수학적으로 완벽하고 정확한 해를 제공합니다. > 한계: 대수적인 풀이법이 알려져 있지 않은 방정식(예: cos(x) = x 또는 eˣ = x+2)은 풀 수 없습니다. --- 2단계: 수치적 해법 (Numerical Solver) - '문제 해결 공학자'의 접근 만약 1단계의 '순수 수학자'가 "이건 공식으로 풀 수 없어"라고 결론 내리면, solve 기능은 포기하지 않고 2단계인 '문제 해결 공학자'에게 문제를 넘깁니다. 이 단계의 목표는 정확한 해는 아니더라도, 매우 정밀한 근사해를 찾는 것입니다. 1. 반복적 탐색: 수치적 해법은 방정식을 직접 푸는 것이 아니라, 해가 있을 만한 지점에서부터 시작하여 반복적인 계산을 통해 해에 점점 더 가까워지는 방식을 사용합니다. * 적당한 값을 추측해서 대입해 봅니다. * 결과가 0보다 큰지 작은지에 따라, 다음 추측값을 어느 방향으로 수정할지 결정합니다. * 이 과정을 수없이 반복하여 오차가 거의 0에 가까워질 때까지 해를 좁혀나갑니다. 2. 핵심 알고리즘: 이때 사용되는 대표적인 알고리즘은 다음과 같습니다. * 뉴턴-랩슨법 (Newton-Raphson Method): 미분(접선)을 이용하여 매우 빠른 속도로 해에 수렴하는 강력한 방법입니다. * 이분법 (Bisection Method): 해가 존재하는 특정 구간을 계속 절반으로 나누어 범위를 좁혀나가는 방식으로, 속도는 느리지만 안정적으로 해를 찾을 수 있습니다. 3. 결과: 이 단계가 성공하면, 시스템은 0.739085133215 와 같이 소수점 아래 여러 자리까지 표현되는 매우 정밀한 부동소수점 형태의 근사해를 반환합니다. > 강점: 대수적으로 풀 수 없는 복잡한 방정식의 해도 근사적으로 찾아낼 수 있습니다. > 한계: 근사해이며, 알고리즘의 특성상 특정 조건(예: 해가 중근을 갖는 경우)에서는 해를 찾지 못하고 실패할 수도 있습니다. 결론: 왜 하이브리드 방식인가? 분석 → 기호적 풀이 시도 → (실패 또는 불가능 시) → 수치적 풀이로 전환 이처럼 현대 CAS의 solve 기능은 정확성(기호적 해법)과 범용성(수치적 해법)이라는 두 마리 토끼를 모두 잡기 위해 설계된 정교한 협력 시스템입니다. 먼저 가장 이상적인 '정확한 해'를 추구하되, 그것이 불가능할 경우 차선책으로 '정밀한 근사해'라도 찾아내어 사용자에게 최대한의 결과를 제공하는 것입니다. 2025 10.17 hp prime 이 solve 함수에서 해를 찾는데 어떤 방법(method)을 사용하는지 공식적인 무서로 정확하게 파악되진 않습니다. 2025 10.17 참고 x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을 x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯? 2025 10.17