- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
인공지능 바둑 프로그램 수준이 많이 올라갔네요.
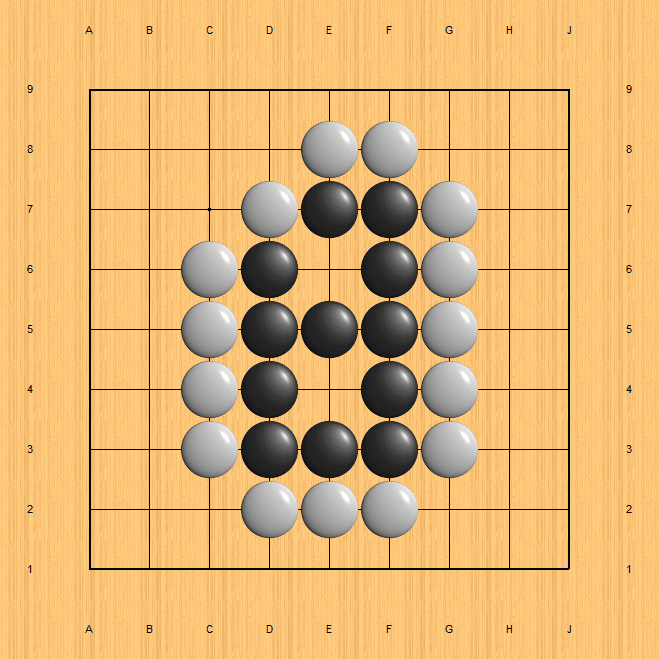
천하수담, 은별 나올 때까지만 기억하고 잊고 있었는데, 그 사이에 몬테 카를로 기법을 도입한 AI 바둑 프로그램이 대세가 되어 있었나봐요. 기력도 부쩍 뛰어서 지금은 상당한 수준에 올라왔나보더라구요. PC 발전도 한 몫 한 것 같구요.
https://ko.wikipedia.org/wiki/%EB%AA%AC%ED%85%8C%EC%B9%B4%EB%A5%BC%EB%A1%9C_%EB%B0%A9%EB%B2%95
체스 프로그램에 딥 블루가 이용되었던 것처럼 (여러 컴퓨터 시스템을 하나로 연결한)클러스터링 PC를 구축해서 두면, 최상급의 프로그램인 경우 아마 4~5단 정도는 둘 수 있는 것 같습니다. (컴퓨터 상태 및 세팅에 따라 기력이 달라질 수 있습니다.)
- 최상급(아마 4단~5단, 클러스터급에서) : ZEN(일본), 돌바람(한국), Crazy Stone(프랑스), Pachi
- 중급(2급, 아마도 일반 데스크탑에서?) : Fuego
- 하급(7급, 아마도 일반 데스크탑에서?) : GNUgo
※ 기력은 국가별/서버별로 측정 기준이 다를 수 있는데, 그것이 적절하게 반영되지 않은채 인터뷰/언급된 것일 수도 있습니다. 참고하시기 바랍니다.
몬테카를로 방법은 바둑의 기본 원리와는 무관하게 (수많은) 결과들을 보고 뒤로 거슬러서 현재의 상황에서 어떤 수가 좋은지를 판단하는 만큼 바둑의 발전과는 무관하다고 볼 수 있는데, 바둑의 기본원리에 기초한 정밀한 알고리즘을 짜는 것은 원래부터 불가능한 것이었을까요? 한계에 부딛힌 것인지... 일시적으로 다른 기법에 밀려서 주춤한 것인지 잘 모르겠습니다. 여튼 현재의 대세는 몬테카를로인가봅니다. 하지만 바둑 원리를 적용하지 않고, 들입다 random 계산만 올리는 방법만으로는 한계에서 조금도 나아가지 못할 겁니다.
댓글13
-
세상의모든계산기
컴퓨터 AI 프로그램 공식 사이트 & 최신 버전
- 은성기위 16 (구 은별바둑) : http://www.silverstar.co.jp/02products/kgigo/kgigo.html
(상업용 )
NK 제품인가? 수출 문제로 일본에서만 판매되는 것으로 보임. (일본어 버전 Only?)
구 버전은 언어문제로 한글윈도우에 설치되지 않기도 하였다고 함. 복잡한 문제는 아니지만... 불편한 것은 사실.
- ZEN : http://soft.mynavi.jp/pcigo/tencho3/index.html
(상업용 11509 Yen) Zenith of Go 5, December 13, 2013
- Crazy Stone : http://www.remi-coulom.fr/CrazyStone/
(상업용 $80) Ver 2013, http://www.unbalance.co.jp/english/software/
- 돌바람 : 없음
- Pachi : http://pachi.or.cz/
(오픈소스) Ver 11. Apr 14, 2015
- Fuego : http://fuego.sourceforge.net/
(오픈소스) Ver 1.1, 2013-11-12
Ver2.0 개발중? http://sourceforge.net/p/fuego/wiki/Fuego%20Release%20Checklist/
- GNUgo : https://www.gnu.org/software/gnugo/
(오픈소스) Ver 3.8, February 19, 2009
- 은성기위 16 (구 은별바둑) : http://www.silverstar.co.jp/02products/kgigo/kgigo.html
-
세상의모든계산기
[컴퓨터의 성능과 기력의 관계]
1. Pachi 소개 문서(2011)에 따르면,
Regularly plays on the internet; KGS:
3 dan on cluster, 1 dan on single machine1 thread weaker than Fuego, but scales better (multi-threaded ≥ Fuego)
2. Pachi Ver 11 의 설명서(README)에 따르면
The default engine plays by Chinese rules and should be about 7d KGS strength on 9x9. On 19x19 (using e.g. six-way Intel i7), it can hold a solid KGS 2d rank. When using a large cluster (64 machines, 20 cores each), it maintains KGS 3d to 4d and has won e.g. a 7-stone handicap game against Zhou Junxun 9p.
3. 그리고 기력 비교표에 따르면,
Japan China Korea[4] Europe[3] AGA KGS IGS Wbaduk[5] DGS OGS FICGS Tygem[6] 1k 3k 5k 4k 1k 2k 3k 6-2k 4k 4k 3k 1d 1d 2k 4k 3k 1d 1k 2k 4-1k 3k 3k 2k 2d 2d 1k 3k 2k 2d 1d 1k 2k-2d 2k 2k 1k 3d 3d 1d 2k 1k 3d 2d 1d 1-3d 1k 1k 1k 3d 4d 2d 1k 1d 4d 3d 2d 2-4d 1d 1d 1d 4d 4d 3d 1d 2d 5d 4d 3d 3-5d 2d 2d 1d 5d 4. Crazy Stone의 홍보 문구에 따르면
2014-03-24: Recently, Crazy Stone established a solid 6-dan rank on KGS, took the second place of the 7th UEC Cup, and won in the Densei-sen in a 4-stone game againstNorimoto Yoda.
5. 결론
단독형 컴퓨터(2016년 현재 상급수준의 가정용 컴퓨터)와 클러스터 컴퓨터를 비교하면, 당연히 클러스터 쪽의 기력이 좋긴 하겠지만, 위 자료를 분석하면 어느 정도의 수준에 다다르면(i7 CPU×2 정도??), 그 이상의 투자대비 효율은 급격하게 떨어질 것으로 추정할 수 있을 것 같음.
-
세상의모든계산기
KGS 서버에서 매월 열리는 AI 간 대결에 사용되는 컴퓨터 사양
http://www.weddslist.com/kgs/past/119/index.htmlDetails of processor numbers, power, etc.
- abakus
- abakus, running on
8 nodes
each with two Intel Xeon E5-2670, 2.6GHz and 64 GByte main memory (128 cores total)
and each with a Tesla K20 (8 GPUs total). - AyaMC
- Aya, using GPU for 12-layer DCNN,
running on Xeon W3680 3.3GHz 6 cores + GTX 980, 6 threads. - darkfmcts3
- Darkforest running on
"10 gpu machines" – further information will appear here when more is known - DolBaram
- DolBaram, running on
Amazon EC2 C4.8xLarge (2.9GHz * 18core) - gnugo3pt8
- GNU Go, version 3.8, running
one thread on one i5-5200 CPU. - WeakBot
- HiraBot running on
an i7-4790k 4 cores 8 threads. HiraBot use neural network data. - YKDbot
- GREAT, running on
an Intel i7-3930K 3.20GHz - Zen19S
- Zen, running on
a mini cluster of - a dual 12-core Xeon E5-2690 v3@2.6 GHz 32 GB RAM,
a dual 10-core Xeon E5-2690 v2@3 GHz 32 GB RAM,
a dual 6-core Xeon X5680@3.5 GHz 12 GB RAM and
an 8-core Core i7 5690X@2.8 GHz 16 GB RAM computers.
Connected via a GbE LAN. 64 cores total.
-
세상의모든계산기
오늘 기사가 하나 올라왔습니다.
http://www.yonhapnews.co.kr/bulletin/2016/01/27/0200000000AKR20160127182600017.HTML?input=feed_daum
http://www.hani.co.kr/arti/economy/it/728244.html
'알파고' 라는 프로그램이 유럽 바둑 챔피언이자 중국 프로 바둑기사인 판후이(2단)와 다섯 차례의 대국에서 핸디캡 없이 모두 이겼고, 이번에는 이세돌 사범과 맞바둑을 둔다고 합니다. -
세상의모든계산기
* 알파고 공식 사이트 : http://www.deepmind.com/alpha-go.html
세부 정보 (From Nature PAPER)
- https://storage.googleapis.com/deepmind-data/assets/papers/deepmind-mastering-go.pdf (링크 짤린듯)
- https://gogameguru.com/i/2016/03/deepmind-mastering-go.pdf
- https://vk.com/doc-44016343_437229031?dl=56ce06e325d42fbc72
- 알고리즘
"We also introduce a new search algorithm that combines Monte-Carlo simulation with value and policy networks."
- 장비
"The final version of AlphaGo used 40 search threads, 48 CPUs, and 8 GPUs. We also implemented a distributed version of AlphaGo that exploited multiple machines, 40 search threads, 1202 CPUs and 176 GPUs."
- 성능 (기력)
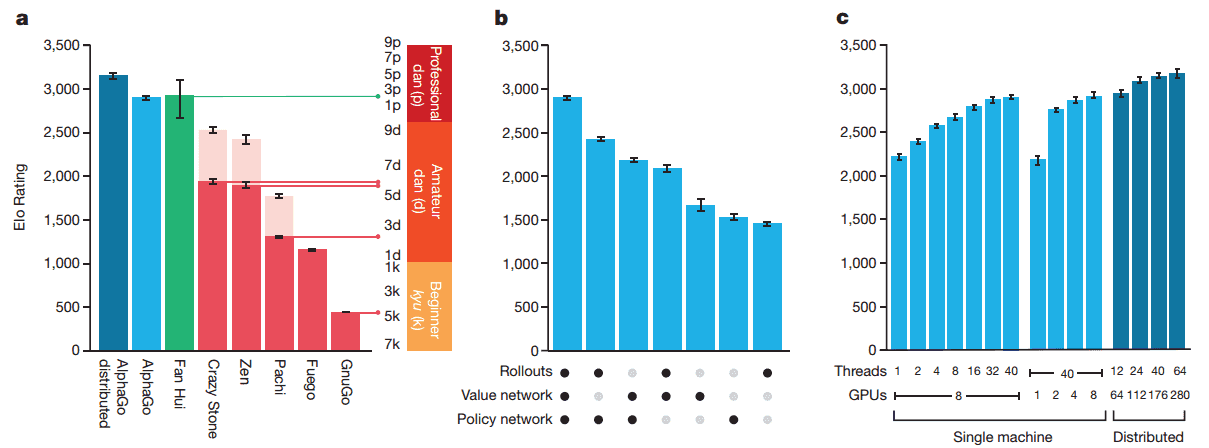
참고 : 이세돌의 ELO Rating http://www.goratings.org/players/5.html
-
세상의모든계산기
대전상대 정보 (Fan Hui 3단)
http://gobase.org/information/players/?pp=Fan%20Hui
http://senseis.xmp.net/?FanHui
Fan Hui (born 1981) is a naturalized French 2-dan professional Go player, originally from China. Fan has been a resident in France since November 2000.
Fan learned to play at age 7 in Xi'an and became a 1-dan professional at 16. He started to study in Toulouse in September 2002.
Fan was the winner of the Paris (2001/2002/2003/2004/2005/2008) and Amsterdam tournaments. He won the EGC [ext] 2013 tournament with a 10/10 result, and won the title of European Champion in 2014 and 2015
In 2005 he became the official instructor of the French Go Federation as a fulltime contractor on their payroll, a role which ended in 2014.
Plays on KGS as fanhui. A section of his book on shape l'âme du go is available in English on SL!


세상의모든계산기 님의 최근 댓글
수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17 Gemini-2.5-pro 답변 ✦ 현대 컴퓨터 대수 시스템(CAS) 계산기에 탑재된 solve 기능의 일반적인 내부 동작 원리에 대해 설명해 드리겠습니다. 현대 CAS의 solve 기능은 단순히 하나의 알고리즘으로 작동하는 것이 아니라, 마치 '순수 수학자'와 '문제 해결 공학자'가 협력하는 것처럼, 여러 단계에 걸친 정교한 '하이브리드(Hybrid)' 방식으로 동작합니다. solve 함수의 작동 과정 1단계: 기호적 해법 (Symbolic Solver) - '순수 수학자'의 접근 계산기는 가장 먼저 방정식을 대수적으로, 즉 정확한 수학적 해를 찾으려고 시도합니다. 이 단계는 마치 사람이 공식을 이용해 문제를 푸는 과정과 같습니다. 1. 방정식 분석: solve 명령을 받으면, 시스템은 먼저 입력된 방정식의 구조를 분석합니다. (예: 이것이 다항식인가? 삼각방정식인가? 로그방정식인가?) 2. 규칙 기반 풀이: 분석된 구조에 따라, 시스템은 내장된 방대한 수학 규칙 라이브러리를 적용합니다. * 선형/이차 방정식: ax+b=c 나 ax²+bx+c=0 같은 형태는 이항, 인수분해, 근의 공식 등을 이용해 즉시 풉니다. * 고차 다항식: 인수분해, 조립제법 등의 규칙을 적용하여 유리수 해를 찾습니다. * 삼각방정식: sin(x) = 0.5 와 같은 경우, x = nπ + (-1)ⁿ * (π/6) 와 같이 주기성을 고려한 일반해 공식을 적용합니다. * 기타: 로그, 지수 법칙 등 해당 방정식에 맞는 대수적 풀이법을 총동원합니다. 3. 결과: 이 단계에서 해를 찾으면, 1.414... 와 같은 근사값이 아닌 √2 나 π/3 와 같은 정확한 기호 형태의 해를 반환합니다. > 강점: 수학적으로 완벽하고 정확한 해를 제공합니다. > 한계: 대수적인 풀이법이 알려져 있지 않은 방정식(예: cos(x) = x 또는 eˣ = x+2)은 풀 수 없습니다. --- 2단계: 수치적 해법 (Numerical Solver) - '문제 해결 공학자'의 접근 만약 1단계의 '순수 수학자'가 "이건 공식으로 풀 수 없어"라고 결론 내리면, solve 기능은 포기하지 않고 2단계인 '문제 해결 공학자'에게 문제를 넘깁니다. 이 단계의 목표는 정확한 해는 아니더라도, 매우 정밀한 근사해를 찾는 것입니다. 1. 반복적 탐색: 수치적 해법은 방정식을 직접 푸는 것이 아니라, 해가 있을 만한 지점에서부터 시작하여 반복적인 계산을 통해 해에 점점 더 가까워지는 방식을 사용합니다. * 적당한 값을 추측해서 대입해 봅니다. * 결과가 0보다 큰지 작은지에 따라, 다음 추측값을 어느 방향으로 수정할지 결정합니다. * 이 과정을 수없이 반복하여 오차가 거의 0에 가까워질 때까지 해를 좁혀나갑니다. 2. 핵심 알고리즘: 이때 사용되는 대표적인 알고리즘은 다음과 같습니다. * 뉴턴-랩슨법 (Newton-Raphson Method): 미분(접선)을 이용하여 매우 빠른 속도로 해에 수렴하는 강력한 방법입니다. * 이분법 (Bisection Method): 해가 존재하는 특정 구간을 계속 절반으로 나누어 범위를 좁혀나가는 방식으로, 속도는 느리지만 안정적으로 해를 찾을 수 있습니다. 3. 결과: 이 단계가 성공하면, 시스템은 0.739085133215 와 같이 소수점 아래 여러 자리까지 표현되는 매우 정밀한 부동소수점 형태의 근사해를 반환합니다. > 강점: 대수적으로 풀 수 없는 복잡한 방정식의 해도 근사적으로 찾아낼 수 있습니다. > 한계: 근사해이며, 알고리즘의 특성상 특정 조건(예: 해가 중근을 갖는 경우)에서는 해를 찾지 못하고 실패할 수도 있습니다. 결론: 왜 하이브리드 방식인가? 분석 → 기호적 풀이 시도 → (실패 또는 불가능 시) → 수치적 풀이로 전환 이처럼 현대 CAS의 solve 기능은 정확성(기호적 해법)과 범용성(수치적 해법)이라는 두 마리 토끼를 모두 잡기 위해 설계된 정교한 협력 시스템입니다. 먼저 가장 이상적인 '정확한 해'를 추구하되, 그것이 불가능할 경우 차선책으로 '정밀한 근사해'라도 찾아내어 사용자에게 최대한의 결과를 제공하는 것입니다. 2025 10.17 hp prime 이 solve 함수에서 해를 찾는데 어떤 방법(method)을 사용하는지 공식적인 무서로 정확하게 파악되진 않습니다. 2025 10.17 참고 x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을 x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯? 2025 10.17