- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
수식 입력기(ckeditor - wiris) 설치 테스트
1. MathJax 문제 발생
기존에 MathJax 를 스크립트로 헤더에 추가하여 수식을 표시하도록 하였습니다. 일반 유저의 경우 문제가 없었던 것으로 파악이 되는데...(아무도 사용을 안했으니까... -_-) 관리자 ID로 로그인하면 MathJax 수식 로딩시 엄청 버벅거리면서 20초가량 사이트 이용이 거의 불가능한 상태가 되곤 하였습니다.
그 문제가 해결될 기미가 없어(=문제를 해결할 수 없어) 기존 방식을 과감하게 포기하였습니다.
대신 ckeditor 에 플러그인으로 수식 편집기를 추가하였습니다. 이 플러그인은 네이버 지식인처럼 수식을 그림으로 넣어줍니다. 기존 방식의 라텍스 문법 입력도 가능합니다.
※ 간혹 (아래처럼) 수식 변환이 되지 않는 경우가 있습니다.
동영상 로딩등으로 페이지 인코딩이 길어질 때인데, 수식을 확인하시려면 F5 (refresh) 제대로 표시될 수 있습니다.
 ⇒
⇒ 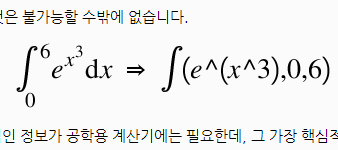
2. 수식 편집기 사용 방법
- ckeditor 입력창의 오른쪽 위에 있는 툴바 확장 단추
 클릭
클릭
└ 툴바가 이미 펼쳐진 상태면 클릭할 필요가 없습니다.
- 툴바 마지막 줄에 있는 노란 루트기호
 클릭
클릭
- wiris 수식 편집기에서 수식 입력후 【승인】 클릭
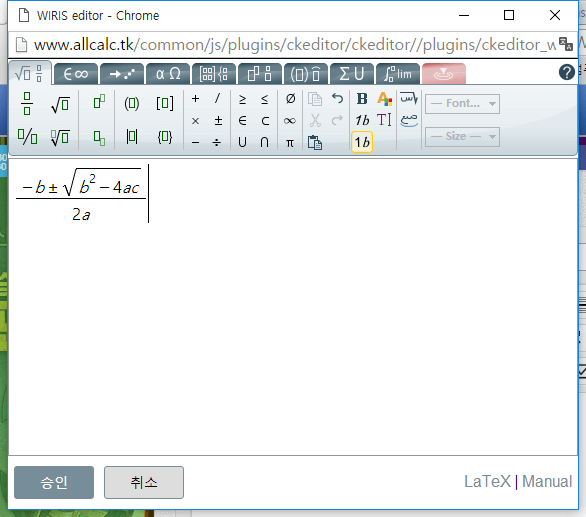
- 수식이 ckeditor에 잘 삽입 되었으면 글을 완성하고 【등록】. 끝.
3. 수식 입력 예제
* Wiris 수식
// 2차방정식 근의 공식
// 기존 MathJax는 수식과 게시판 text 를 한 줄에 넣을 수 없었는데 이젠 가능.
* MathJax 수식
// 에디터에서 쓸 때는 MathJax 수식이지만 뷰어에서 보여줄 때는 Wiris 에서 이미지로 처리하도록 바뀜
혹시 위의 수식이 제대로 표시되지 않는다면 【F5】 로 페이지를 새로고침 해보세요.
댓글11
-
세상의모든계산기
댓글 수식 test (실제):
1. Wiris 를 통한 입력 ▶▶▶
2. 기존 MathJax 방식 입력 ▶▶▶
위(↑)의 수식 표시 화면이
아래와 같이 표시(브라우저 Rendering)되면 성공
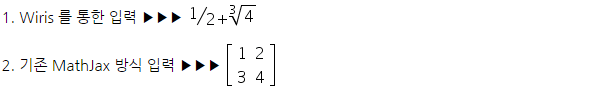
아래와 같이 표시(브라우저 Rendering)되면 실패
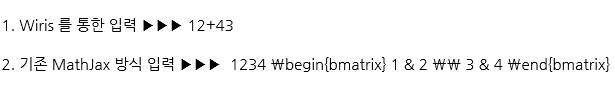
-
세상의모든계산기
브라우저별 수식 표시 가능성 비교
본문 댓글 Wiris MathJax Wiris MathJax 크롬47(PC) O O O O 크롬(모바일) O O O O 오페라34(PC) O O O O FireFox43* O O O O Safari5* O O O O EDGE(Win10) O X⇒ OX⇒ OX⇒ OIE11(Win10) O X⇒ OX⇒ OX⇒ O
* 표시된 브라우저는 https://spoon.net/ 을 통해서 간접 측정하였습니다.
EDGE 와 IE11 은 약간의 문제가 있었지만 script sync 방식을 defer로 변경하여 문제를 해결하였습니다. -
세상의모든계산기
CAS계산기
√ 버튼 옆에 있는 = 버튼은 CAS계산기입니다.
JAVA 프로그램이므로 크롬과 오페라(NPAPI 지원중단)에서는 사용이 불가능합니다.
(IE, 파이어폭스에서는 사용 가능합니다)잠깐 써 봤는데, 생각보다는 꽤 괜찮지만, 로딩이 매우 느리고, 안정성도 조금 부족한 것 같습니다.
(회원 등급에 따라 붙여넣기 해도 안보일 수 있으니 가급적 사용을 자제하여 주시기 바랍니다.)버튼을 누르면 이렇게 계산기 창이 뜹니다.
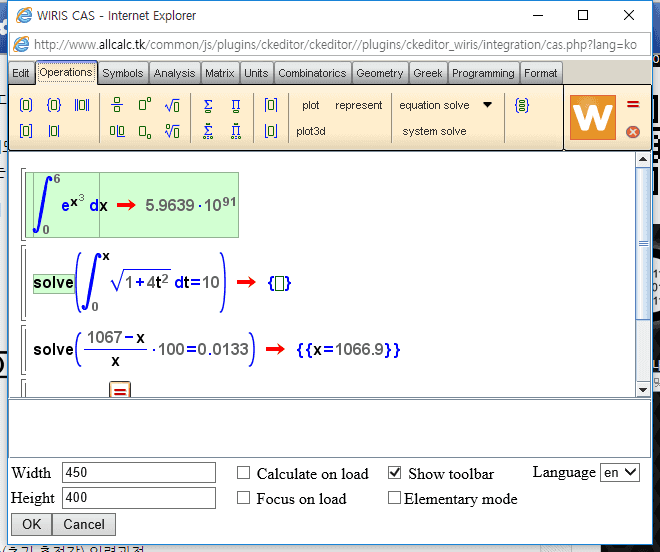
계산식을 모두 입력 완료하고 OK 버튼을 누르면 사이즈에 맞는 계산기가 입력이 됩니다.
이미지 파일이 링크됩니다. 그런데 alt 형식으로 계산식 (애플릿 스크립트) 자체가 로딩될 수도 있습니다.
글 입력한 사람 뿐 아니라, 다른 사람도 해당 계산기를 이용할 수 있긴한데...
크롬 유저는 (현 상황으로는) 그림도/계산기도 볼 수 없으니...
계산기를 그대로 입력하는 방식은 가급적 사용을 자제해 주셨으면 합니다. -
세상의모든계산기
계산기를 넣은 다음 소스보기를 하면 굉장히 긴 이미지 링크가 나오는데,
중간을 삭제하면 계산기 애플릿은 로딩되지 않고 이미지만 링크가 되어서 모든 브라우저에서 볼 수가 있습니다.

이렇게요.

-
세상의모든계산기
지금 보니까 CAS 계산기가 안열리네요. (크롬, IE 모두)
PC에 JAVA 는 설치되어 있는데 JAVA 가 필요need 하다고 나오는 상황...
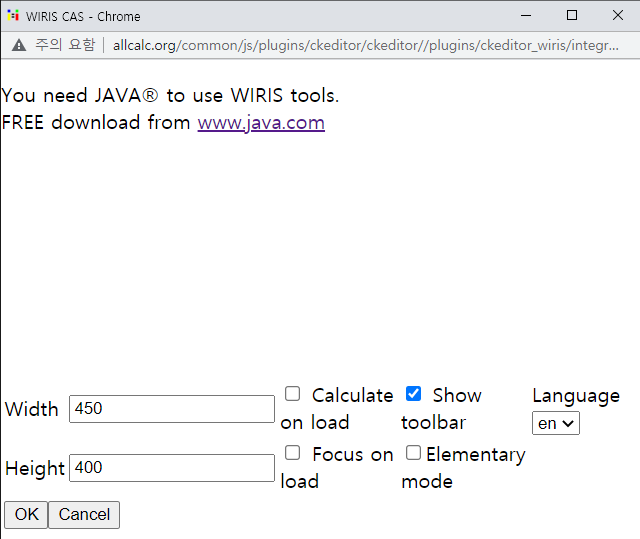
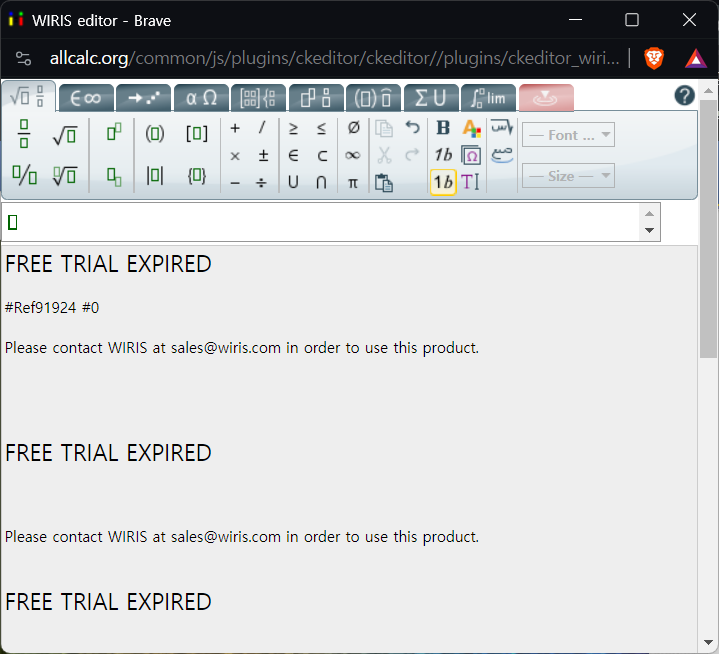
활용도가 떨어지고, 개발자도 버린 듯 하니... 일단 사용 안하는 걸로 변경!
하려고 했는데, 아이콘 하나만 빼는 것은 안되는 듯.


세상의모든계산기 님의 최근 댓글
수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17 Gemini-2.5-pro 답변 ✦ 현대 컴퓨터 대수 시스템(CAS) 계산기에 탑재된 solve 기능의 일반적인 내부 동작 원리에 대해 설명해 드리겠습니다. 현대 CAS의 solve 기능은 단순히 하나의 알고리즘으로 작동하는 것이 아니라, 마치 '순수 수학자'와 '문제 해결 공학자'가 협력하는 것처럼, 여러 단계에 걸친 정교한 '하이브리드(Hybrid)' 방식으로 동작합니다. solve 함수의 작동 과정 1단계: 기호적 해법 (Symbolic Solver) - '순수 수학자'의 접근 계산기는 가장 먼저 방정식을 대수적으로, 즉 정확한 수학적 해를 찾으려고 시도합니다. 이 단계는 마치 사람이 공식을 이용해 문제를 푸는 과정과 같습니다. 1. 방정식 분석: solve 명령을 받으면, 시스템은 먼저 입력된 방정식의 구조를 분석합니다. (예: 이것이 다항식인가? 삼각방정식인가? 로그방정식인가?) 2. 규칙 기반 풀이: 분석된 구조에 따라, 시스템은 내장된 방대한 수학 규칙 라이브러리를 적용합니다. * 선형/이차 방정식: ax+b=c 나 ax²+bx+c=0 같은 형태는 이항, 인수분해, 근의 공식 등을 이용해 즉시 풉니다. * 고차 다항식: 인수분해, 조립제법 등의 규칙을 적용하여 유리수 해를 찾습니다. * 삼각방정식: sin(x) = 0.5 와 같은 경우, x = nπ + (-1)ⁿ * (π/6) 와 같이 주기성을 고려한 일반해 공식을 적용합니다. * 기타: 로그, 지수 법칙 등 해당 방정식에 맞는 대수적 풀이법을 총동원합니다. 3. 결과: 이 단계에서 해를 찾으면, 1.414... 와 같은 근사값이 아닌 √2 나 π/3 와 같은 정확한 기호 형태의 해를 반환합니다. > 강점: 수학적으로 완벽하고 정확한 해를 제공합니다. > 한계: 대수적인 풀이법이 알려져 있지 않은 방정식(예: cos(x) = x 또는 eˣ = x+2)은 풀 수 없습니다. --- 2단계: 수치적 해법 (Numerical Solver) - '문제 해결 공학자'의 접근 만약 1단계의 '순수 수학자'가 "이건 공식으로 풀 수 없어"라고 결론 내리면, solve 기능은 포기하지 않고 2단계인 '문제 해결 공학자'에게 문제를 넘깁니다. 이 단계의 목표는 정확한 해는 아니더라도, 매우 정밀한 근사해를 찾는 것입니다. 1. 반복적 탐색: 수치적 해법은 방정식을 직접 푸는 것이 아니라, 해가 있을 만한 지점에서부터 시작하여 반복적인 계산을 통해 해에 점점 더 가까워지는 방식을 사용합니다. * 적당한 값을 추측해서 대입해 봅니다. * 결과가 0보다 큰지 작은지에 따라, 다음 추측값을 어느 방향으로 수정할지 결정합니다. * 이 과정을 수없이 반복하여 오차가 거의 0에 가까워질 때까지 해를 좁혀나갑니다. 2. 핵심 알고리즘: 이때 사용되는 대표적인 알고리즘은 다음과 같습니다. * 뉴턴-랩슨법 (Newton-Raphson Method): 미분(접선)을 이용하여 매우 빠른 속도로 해에 수렴하는 강력한 방법입니다. * 이분법 (Bisection Method): 해가 존재하는 특정 구간을 계속 절반으로 나누어 범위를 좁혀나가는 방식으로, 속도는 느리지만 안정적으로 해를 찾을 수 있습니다. 3. 결과: 이 단계가 성공하면, 시스템은 0.739085133215 와 같이 소수점 아래 여러 자리까지 표현되는 매우 정밀한 부동소수점 형태의 근사해를 반환합니다. > 강점: 대수적으로 풀 수 없는 복잡한 방정식의 해도 근사적으로 찾아낼 수 있습니다. > 한계: 근사해이며, 알고리즘의 특성상 특정 조건(예: 해가 중근을 갖는 경우)에서는 해를 찾지 못하고 실패할 수도 있습니다. 결론: 왜 하이브리드 방식인가? 분석 → 기호적 풀이 시도 → (실패 또는 불가능 시) → 수치적 풀이로 전환 이처럼 현대 CAS의 solve 기능은 정확성(기호적 해법)과 범용성(수치적 해법)이라는 두 마리 토끼를 모두 잡기 위해 설계된 정교한 협력 시스템입니다. 먼저 가장 이상적인 '정확한 해'를 추구하되, 그것이 불가능할 경우 차선책으로 '정밀한 근사해'라도 찾아내어 사용자에게 최대한의 결과를 제공하는 것입니다. 2025 10.17 hp prime 이 solve 함수에서 해를 찾는데 어떤 방법(method)을 사용하는지 공식적인 무서로 정확하게 파악되진 않습니다. 2025 10.17 참고 x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을 x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯? 2025 10.17