[공학용 계산기] = 와 ≒ ≈ 의 비교 (equal vs almost equal)
1. equal vs almost equal
| = | ≒ or ≈ | |
| 명칭 | equal sign, equality symbol |
approximation sign, approximately equal symbol |
| 의미 |
같다 |
대략 같다 almost equal to approximately equal to |
| 비고 | 방정식이나 함수의 정의를 나타내기 위해 자주 사용 | ≒ 동양권(한국, 일본, 대만 등)에서 주로 사용 ≈ 서양권에서 주로 사용. 더 보편적임. |
역사적 배경 : 출처 (위키) (Quora)
등호 기호(=)는 1557년 로버트 레코드(Robert Recorde)에 의해 처음 소개되었습니다.
그는 자신의 저서 "The Whetstone of Witte"에서 두 평행선이 같음을 의미한다고 설명했습니다.
"≈" 기호는 그 연원에 대해 웹 검색이 되지 않고 있고,
"≒" 기호는 1875년에 Anton Steinhauser 가 이와 유사한 ≐ 기호를 "Is nearly Equal to"로 사용했다는 것이 검색됩니다.
여튼 두 기호는 여러가지 형태로 쓰이다가 비교적 최근에 정립된 기호로 판단됩니다.
학창시절
학창시절... 너무 오래된 기억이라서 정확하진 않은데, 처음 배울 때 두가지 기호 모두에 대해 설명을 들었던 것 같긴 합니다.
처음 배운 이후로 물결(≈) 을 사용해 수식을 적으셨던 선생님은 한분도 안계셨던 것 같습니다.
저도 그 영향인지 평생 ≒ 만 사용했었구요.
여러분들은 어떠신가요?
2. 계산기에서의 근사값 기호의 사용
대부분의 계산기에는 【=】 기호만 있습니다. 기호 대신에 【EXE】 나 【enter】 등의 명령어 버튼이 등호 기능을 담당하기도 합니다.
하지만 이런 계산기에서 【=】 기호가 적힌 버튼을 누른다고 해서 항상 equal 한 결과가 나오는 것은 아닙니다.
equal 한 결과를 낼 수 있다면 equal 한 결과를 도출하겠지만, 불가피한 경우에는 equal 이 아닌 almost equal 한 결과 ≒ 를 얻습니다.
예를 들어 1÷3 을 계산하는데 그 결과로 ⅓ 을 저장하고 출력하지 못하는 계산기는
⅓ 대신 0.3333333333 처럼 일정한 자릿수까지 짤려진 근사값(approximation)을 구하게 됩니다.
특별한 계산기
위에 설명드린 대부분의 계산기와 달리 근사값을 구하는 기능이 따로 구분된 계산기도 있습니다.
(그런데 보통은 ≒ 기호로 적기 보다는 물결표시 ≈ 로 적는 경우가 많습니다. 서구권에서 개발되었기 때문일까요?)
 [TI-nspire]
[TI-nspire]  [HP Prime]
[HP Prime]
이러한 계산기는 대부분 C.A.S 기능이 있는 계산기들로서 참값으로 계산하하도록 하면 정확한 값을 최대한! 우선적으로 찾기 때문에 기호를 포함한 아주 복잡한 수식이 나오기도 합니다.
간단한 수치만 필요한 상황에서 복잡한 수식으로 결과가 나오면 오히려 불편하기만 하므로, 이런 때에는 정확한 값을 찾지말고 대충 비슷한 값을 찾으라고 계산기에 강제로 명령하는 것이 필요합니다.
※ 참값 계산시보다 근사값 계산시 계산 시간이 단축되는 장점도 있습니다.
댓글5
-
세상의모든계산기
유사 기호
≠ : 같지 않음을 나타내는 기호로, 두 값이 동일하지 않음을 의미합니다. (U+2249)
≡ : 항등 기호로, 두 표현식이 항상 동일함을 나타냅니다. 주로 논리학 및 수학에서 사용됩니다. (U+003D)
∝ : 비례 기호로, 한 값이 다른 값에 비례함을 나타냅니다.
https://math.stackexchange.com/questions/864606/difference-between-%E2%89%88-%E2%89%83-and-%E2%89%85
- ≈ : ALMOST EQUAL TO (U+2248)
- ≃ : ASYMPTOTICALLY EQUAL TO (U+2243)
- ≅ : APPROXIMATELY EQUAL TO (U+2245)
Some Common Mathematical Symbols and Abbreviations (with History) Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (January 21, 2007)
:=

-
세상의모든계산기
A History of Mathematical Notations,
저자: Florian Cajori
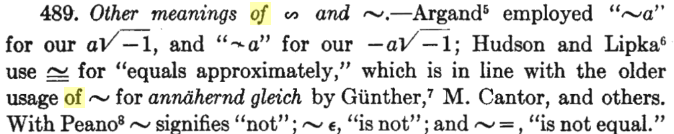


-
세상의모든계산기
https://mathshistory.st-andrews.ac.uk/Miller/mathsym/relation/
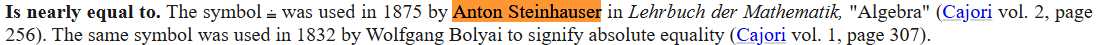
Cajori_Florian_A_History_of_Mathematical_Notations_2_Vols.pdf



세상의모든계산기 님의 최근 댓글
ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28 자게로 이동조치하였습니다. 그리고 이 글의 내용을 정리하여 HP 포럼에 올려두었습니다. https://allcalc.org/55774 [HP Prime] Solve 함수 사용법 2025 10.27 수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데... 위의 스샷을 보면 되는 듯 하면서도 아래 스샷을 보면 안되는 것 같기도 합니다. solve(Expr,[Var]) csolve(LstEq,LstVar) nSolve(Expr,Var,[Guess or Interval],[Method]) deSolve(Eq,[TimeVar],FncVar) linsolve(LstLinEq,LstVar) fsolve(Expr,Var,[Guess or Interval],[Method]) 2025 10.17 종합해서 답변을 드리면 HP Prime 에 solve 에서 변수명에 구간을 입력하면 수치해석 방식으로 bisection 을 사용함. 이 bisection 방식은 해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고 해의 좌-우 부호가 같으면 해를 인식하지 못합니다. 이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다. 2025 10.17