[공학용 계산기] 정적분 계산 속도 벤치마크 비교
-
- 2021.07.27 - 19:28 2015.11.04 - 09:32 5476 10
계산기는 계산을 하는 도구이고, 계산의 중심에는 CPU 가 있습니다. CPU 의 종류에 따라 속도는 천차만별일 수 있습니다. 유튜브 동영상중에 공학용 계산기 CPU 성능을 비교 벤치마크한 것이 있습니다. 정밀한 벤치마크는 아닙니다.
[주의] 벤치마크에 사용한 수식은 정적분인데요. 수치해석적으로 계산하는 방법과 부정적분 후 계산하는 방법(CAS계산기)이 있습니다. 수치해석적으로 계산할 때는 계산 횟수가 굉장히 많은 편이라서 CPU 성능이 좋지 않으면 시간이 꽤 오래걸리게 됩니다. 하지만 부정적분을 먼저 하고 구간을 대입하는 계산방식이라면, 계산이 몇회만에 끝나기 때문에 CPU 성능을 측정하는데는적합하지 않습니다.
- 아래에 사용된 수식은 부정적분으로 식이 쉽게 정리되는 꼴이 아니므로, 큰 문제는 없는 듯 합니다만...
식1) "(e^(x^3)) 함수를 0에서 6까지 정적분"하는 계산에 걸리는 시간을 측정하였습니다.
그 정확한 결과값은 울프람 알파를 참조하시구요. 대략적으로 5.9639380918993E91 이 나옵니다.
결과값을 얻는데 걸리는 시간은 각각 아래와 같습니다.
| 제조사 | 모델명 | 식1) | 식2) |
| CASIO | fx-9860G II | 0:06 | |
| fx-CG10 | 0:04.5 | ||
| fx-570 ES (PLUS) | 2:00 | 3:28 | |
| fx-570 EX fx-991 EX |
0:25 | 0:37 | |
| ClassPad II | 0:03 | ||
| TI | 36X Pro | 1:48 | 01:01 |
| nSpire CX | ＜0:01 | ||
| nSpire CX II | |||
| 89 Titanium | 0:14 | ||
| 84 Plus SE | 0:07 | ||
| HP | 50G | 1:05 |
EXACT |
| Prime | ＜0:01 | ||
| 39gII | Error | 0:08 | |
| 35s | 15:30 and ERROR |
| 제조사 | 모델명 | 식1) | 식2) |
| CASIO | F-7899GA | 기록 없음 | 4:40 |
| fx-9750gIII | 0:04 | 0:05.5 | |
- 최신 CAS 급 계산기들은 걸리는 시간이 몇 초 이내라서 벤치마크 판별력이 없습니다.
- [TI-89T] 와 [HP50G] 가 예상외로 상당히 부진한 결과를 보여줍니다. 계산 방식(정확성)의 차이가 아닐까 싶지만 정확한 이유는 모르겠습니다.
-
25
댓글10
-
세상의모든계산기
실물 계산기가 아닌 PC용 에뮬의 속도는? (확실히 실물보다 빠르네요)
[fx-570 ES PC Emul]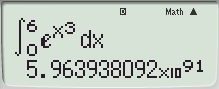 
- 15초~20초
[fx-570 EX PC Emul]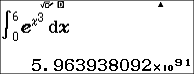 
- 대략 10초
[fx-570 MS PC EMUL] 
- 1초 이내
- 그런데 오차가...
-
세상의모든계산기
SHARP\EL_W506_W516_W546_v110 PC Emul
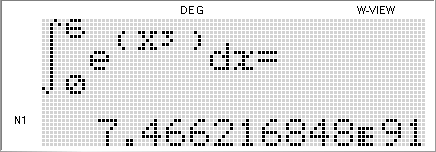
- 2~3초
- 오차 후덜덜
-
세상의모든계산기
* 또 다른 Benchmark : Casio fx-991 DE X classwiz vs. fx-991 ES
계산식 2) :
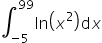
991 ES : 3 Min 28 Sec
991 EX (Classwiz) : 37 Sec동영상 댓글 내용에 의하면
ijabbott63 3개월 전(수정됨)
Thanks. For comparison, I ran the same benchmark on some other calculators:
TI-36X Pro - 01:01
Casio fx-115ES PLUS - 02:50
Canon F-789SGA - 04:40
HP 35s ('ALL' display) - ran for 15:30 before returning the error "NONEXISTENT" -
세상의모든계산기
참값은 198*ln(99)+10*ln(5)-208 = 99*ln(9801)+10*ln(5)-208 인데,
근사값은 정확하게 확인하지 못했습니다만, 울프람갓을 정답이라고 가정하면...Wolfram Alpha : 717.928109450989 ±0.000000000000
HP Prime : 717.928109450887 -0.000000000102
fx-9860G : 717.928109450611 -0.000000000378
fx-570 ES P : 717.92810945059 -0.000000000399
TI-nspire : 717.92810934465 -0.000000106339
TI-89T : 717.92810934465 -0.000000106339
TI-84 : 717.92812676129 +0.000017310301전반적으로 TI 계열이 상태가 안좋네요.
※ Ans - 717.9281 【=】 계산을 하여 추가자릿수까지 확인한 결과입니다.
원래의 식에 -717.9281 을 더하면 결과가 달라질 수 있습니다. -
세상의모든계산기
HP 39gII 수식2
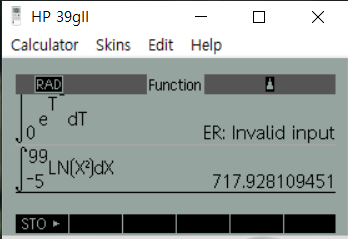
실물 계산기 8초정도 걸리고, PC에뮬은 즉시 나옵니다. -
세상의모든계산기
HP 50g 는
어쩔 때는 Singularity! Continue? 가 나오면서 Exact 결과값이 나오기도 하는데,
또 어쩔 때는 한~~참 후에 근사답이 나오기도 합니다.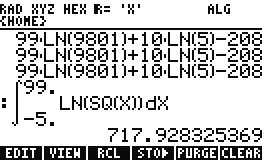
-
세상의모든계산기
hp 39gII 는 수식1에서 에러가 발생하네요(ER: Invalid input)
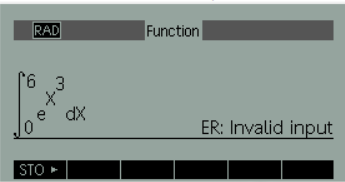
※ 설정상의 문제 같은데... 해결이 안되네요.
세상의모든계산기 님의 최근 댓글
HP-39gII 에 ExistOS 설치하기 https://allcalc.org/38526 2025 11.07 1. 왜 검은색이 아닌 다른 색으로 보일까? (제공된 LUT 필터) 제가 제공해 드린 magenta_lens.cube LUT 필터는 540~560nm(녹색-노란색) 파장대의 색상을 '완전히 제거(검은색으로 만듦)'하는 대신, '다른 색상으로 왜곡/변환'하도록 설계되었습니다. * 원리: LUT(Look-Up Table)는 특정 입력 색상(Input RGB)을 미리 정해진 다른 출력 색상(Output RGB)으로 매핑하는 테이블입니다. 이 LUT는 540~560nm에 해당하는 RGB 값들이 들어오면, 검은색(0, 0, 0)이 아닌, 매우 어둡거나 채도가 낮은 특정 색(예: 어두운 올리브색, 갈색 등)으로 변환하라고 지시합니다. * 의도: * 현실적인 물리 필터 시뮬레이션: 실제 고가의 색약 보정 안경도 특정 파장을 100% 완벽하게 차단하지는 못합니다. 빛의 일부를 흡수하고 일부는 통과시키거나 변환하는데, 이 LUT는 그러한 현실 세계의 필터 효과를 더 비슷하게 흉내 냈을 수 있습니다. * 시각적 정보 유지: 특정 색을 완전히 검게 만들면 그 부분의 형태나 질감 정보가 완전히 사라집니다. 하지만 다른 어두운 색으로 대체하면, 색상 정보는 왜곡되더라도 밝기나 형태 정보는 어느 정도 유지되어 전체적인 이미지가 덜 어색하게 보일 수 있습니다. 결론적으로, 스펙트럼 그림에서 해당 대역의 색이 갑자기 '다른 색으로 툭 바뀌는' 현상은, LUT 필터가 "이 파장대의 색은 앞으로 이 색으로 표시해!"라고 강제적으로 지시한 결과이며, 이것이 바로 이 필터가 작동하는 방식 그 자체입니다. 2. 왜 'Color Vision Helper' 앱은 검은색으로 보일까? 비교하신 'Color Vision Helper' 앱은 노치 필터의 원리를 더 이상적(Ideal)이고 교과서적으로 구현했을 가능성이 높습니다. * 원리: "L-콘과 M-콘의 신호가 겹치는 540~560nm 파장의 빛은 '완전히 차단'되어야 한다"는 개념에 매우 충실한 방식입니다. * 구현: 따라서 해당 파장에 해당하는 색상 정보가 들어오면, 어떠한 타협도 없이 그냥 '검은색(RGB 0, 0, 0)'으로 처리해 버립니다. 이는 "이 파장의 빛은 존재하지 않는 것으로 처리하겠다"는 가장 강력하고 직접적인 표현입니다. 2025 11.06 적용사례 4 - 파장 스펙트럼 https://news.samsungdisplay.com/26683 ㄴ (좌) 연속되는 그라데이션 ➡️ (우) 540 이하 | 구분되는 층(색) | 560 이상 - 겹치는 부분, 즉 540~560 nm 에서 색상이 차단? 변형? 된 것을 확인할 수 있음. 그럼 폰에서 Color Vision Helper 앱으로 보면? ㄴ 540~560 nm 대역이 검은 띠로 표시됨. 완전 차단됨을 의미 2025 11.05 빨간 셀로판지로도 이시하라 테스트 같은 숫자 구분에서는 유사한 효과를 낼 수 있다고 합니다. 색상이 다양하다면 빨강이나, 노랑, 주황 등도 테스트해보면 재밌겠네요. 2025 11.05 안드로이드 앱 - "Color Vision Helper" 다운받아 본문 내용을 카메라로 찍어 보니, 본문 프로그램에서는 애매하게 보이던 부분에서도 구분이 완전 확실하게 되네요. 숫자 구분 능력 & 편의성 면에서 압도적이라고 할 수 있겠습니다. 2025 11.05