- 세상의 모든 계산기 수학, 과학, 공학 이야기 확률통계 ()
신뢰도 함수 R(t) (고장률이 일정할 때)
-
- 2024.06.28 - 15:29 2024.06.28 - 10:40 1535 2
https://m.blog.naver.com/shipbuilding_pro/222239092204
신뢰도 함수 R(t)
신뢰도 함수 R(t)는 시스템이나 부품의 수명 시간 t 동안 신뢰도를 나타내는 함수입니다. 일반적으로 지수 분포나 와이블 분포 등의 확률 분포를 따릅니다. 고장 확률 분포는 시스템이나 부품이 고장 날 확률을 나타내는 분포입니다. 신뢰도 함수 R(t)와 고장 확률 분포는 밀접한 상관관계가 있습니다. 신뢰도 함수 R(t)는 고장 확률 분포를 적분하여 구할 수 있으며, 고장 확률 분포는 신뢰도 함수 R(t)를 미분하여 구할 수 있습니다. 예를 들어, 지수 분포를 따르는 신뢰도 함수 R(t)의 경우, 고장 확률 분포는 지수 분포를 따릅니다. 와이블 분포를 따르는 신뢰도 함수 R(t)의 경우, 고장 확률 분포는 로그 정규 분포를 따릅니다. 이러한 신뢰도 함수와 고장 확률 분포는 시스템이나 부품의 수명을 예측하고, 신뢰성을 평가하는 데 중요한 역할을 합니다.
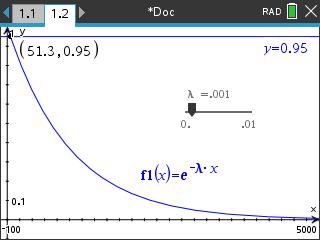
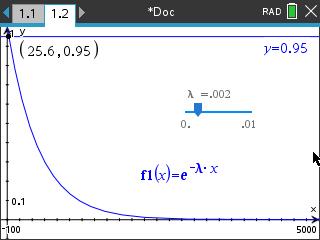
고장률이 일정할 때 사용하는 신뢰도 함수는 지수 분포를 따르며, 이에 대한 공식은 다음과 같습니다. R(t) = e^(-λt) 여기서 λ는 고장률을 의미하며 단위 시간당 고장 확률을 나타냅니다. 고장률이 일정한 경우, 시간이 지남에 따라 신뢰도가 일정한 비율로 감소합니다. 따라서 위의 공식을 이용하여 신뢰도를 계산할 수 있습니다. 더 궁금한 내용이 있으시다면 말씀해 주세요.
=exp(-λ*t) 로 쓰기도 함.
t 는 제품의 사용시간을 나타내고, λ 는 일정한 고장률(=평균고장률)을 나타냄.
신뢰도 함수는 t 시간이 지났을 때, 고장나지 않고 정상품으로 남아있을 확률을 의미한다.
람다 값이 커질수록, 시간당 고장확률이 크다. --> 그래프가 원점에 가까워진다.
-
25
세상의모든계산기 님의 최근 댓글
낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10 마지막 발언이 마지막 힌트이자 문제의 핵심이군요. 처음 들은 달이 8월이었다면 (15일인지 17일인지 확신할 수 없어서) 마지막 대사를 할 수 없지만, 처음 들은 달이 7월이었다면 (선택지가 16일 하나라서 확신이 가능하므로) 마지막 대사를 할 수 있다. 대사를 했으니 7월이다. 이제 이해되었습니다. 지금 보니까 이해가 되는데, 당시에는 왜 이해가 안됐을까요? 세가지 전제 하에 문제를 풀면 A는 마지막 대화 2줄만으로 C의 생일을 알 수 없어야 정상인데, 무슨 이유에서인지 "그럼 나도 앎!"이라고 선언해 버립니다. 알게 된 이유를 대화 속에서 찾을 수는 없습니다. 이 편견에 사로잡혀 빠져나오지 못하고 다른 길로 계속 샜나봅니다. 2025 10.09 (장*훈)님 (+10,000원) 계좌 후원(2025/10/09) 감사 드립니다. 2025 10.09 원래 식이 풀어진 상태에서는 두번째 인수 v가 분모, 분자에 섞여 있어서 계산기가 처리하지 못하는 듯 합니다. 이 때는 위에서와 반대로 분모 부분만 다른 문자(w)로 치환한 다음 completesquare(,v^2) 처리를 하면 일부분은 묶이는 듯 합니다. 하지만 여기서 처음 모양으로 더 이상 진행되진 않네요. 2025 10.08 전체 식에서 일부분(분모, 루트 내부)만 적용할 수는 없습니다. 번거롭더라도 해당 부분만 따로 끄집어 내서 적용하셔야 합니다. https://allcalc.org/30694#comment_30704 2025 10.08