- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
fx-570 ES/EX, solve() 특이 케이스
-
- 2024.06.26 - 03:12 2024.06.07 - 15:00 1896 2
TI-nspire 에서 solve() 함수로
f1(x) = f2(x) 를 만족하는 해를 찾아 보면
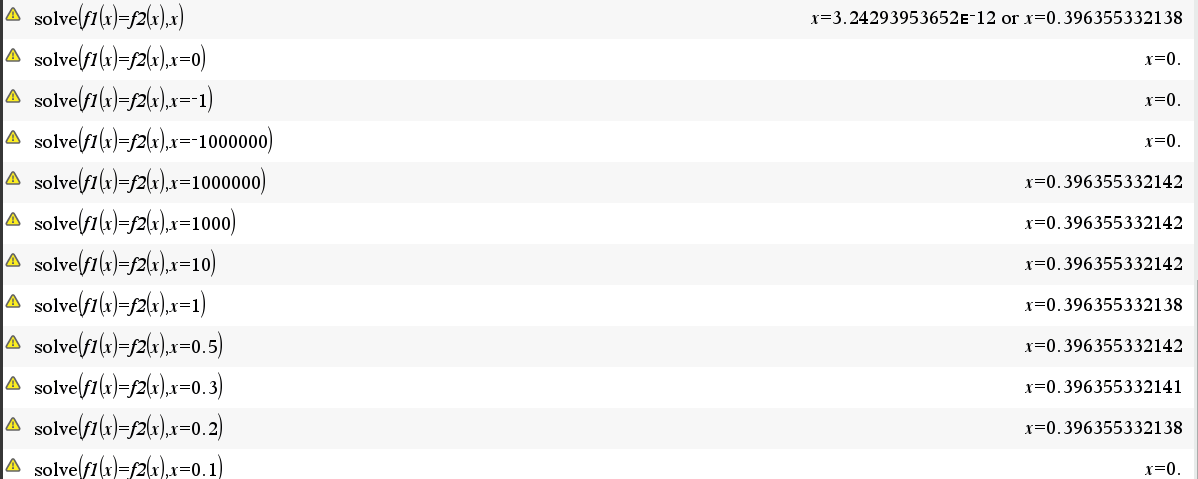
x=0 인 것은 명확해 보이는데,
추정치 없을 때) 처음에 x=0 이 아닌,
x=3.24293953652E−12 를 해 중 하나로 내놓았습니다.
수식에 소숫점이 들어가서 근사 계산으로만 계산했기 때문에 발생한 문제였던 것 같습니다.
추정치를 넣으면, 문제가 발생하진 않네요.
fx-570 ES 시리즈에서
수식 : 18.65(1.47^x-1) - 12.39(1.75^x-1)
기능 : solve
으로 해를 찾아봅니다.
1) 초기값을 0으로 넣으면
x=0.39635533214217 를 건너뛰고
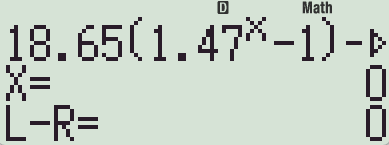
X = 0 을 반환합니다. 건너 뛰는 부분이 좀 특이한 것 같습니다.
2) 초기값을 100으로 넣으면
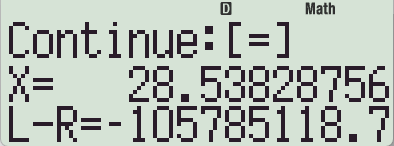
계산 횟수 한계로 중간에 한번 멈추구요. (L-R ≠ 0)
다시 한 번 이어서 【=】 계산하면
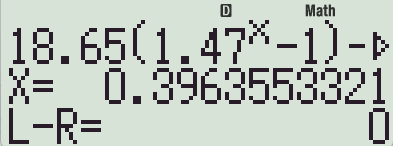
제대로(=건너 뛰지 않고) 해(x=0.3963553321)를 찾아냅니다.
3) 초기값을 10으로 하면
한번에 제대로(=건너 뛰지 않고) 해(x=0.3963553321)를 찾아냅니다.
4) 여기서 수식 형태를 바꿔서 18.65(1.47^x-1) = 12.39(1.75^x-1) 로 입력하면
3)과 같은 초기값 10에서 해(x=0.3963553321)를 건너 뛰고 x=0을 찾네요.
초기값 5에서도 건너 뛰고 x=0 만 반환합니다.
심지어 초기값으로 0.39를 넣어도
(x=0.3963553321) 를 못찾습니다.
이것 참 요상하네요.
혹시나 fx-570 EX 에서 해 봐도 같습니다.
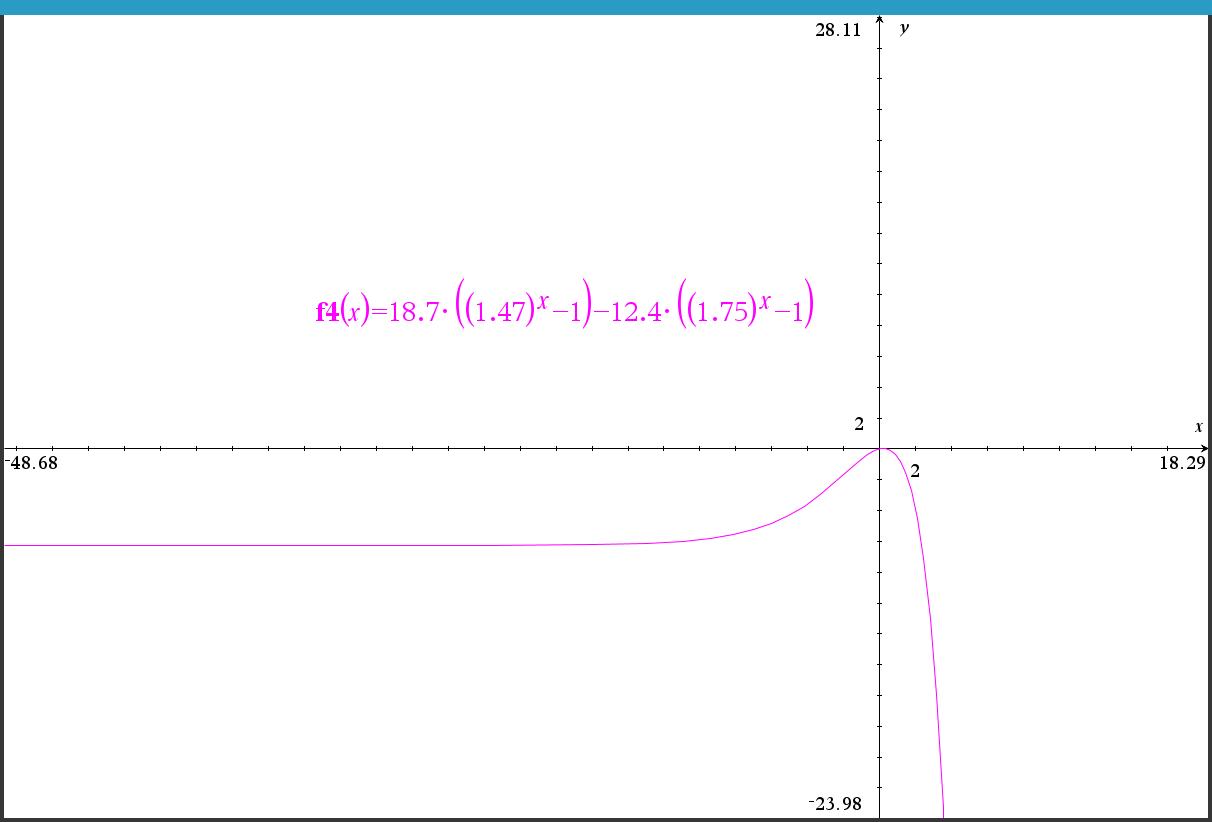
y=0 과 교차점을 줌인해 보면
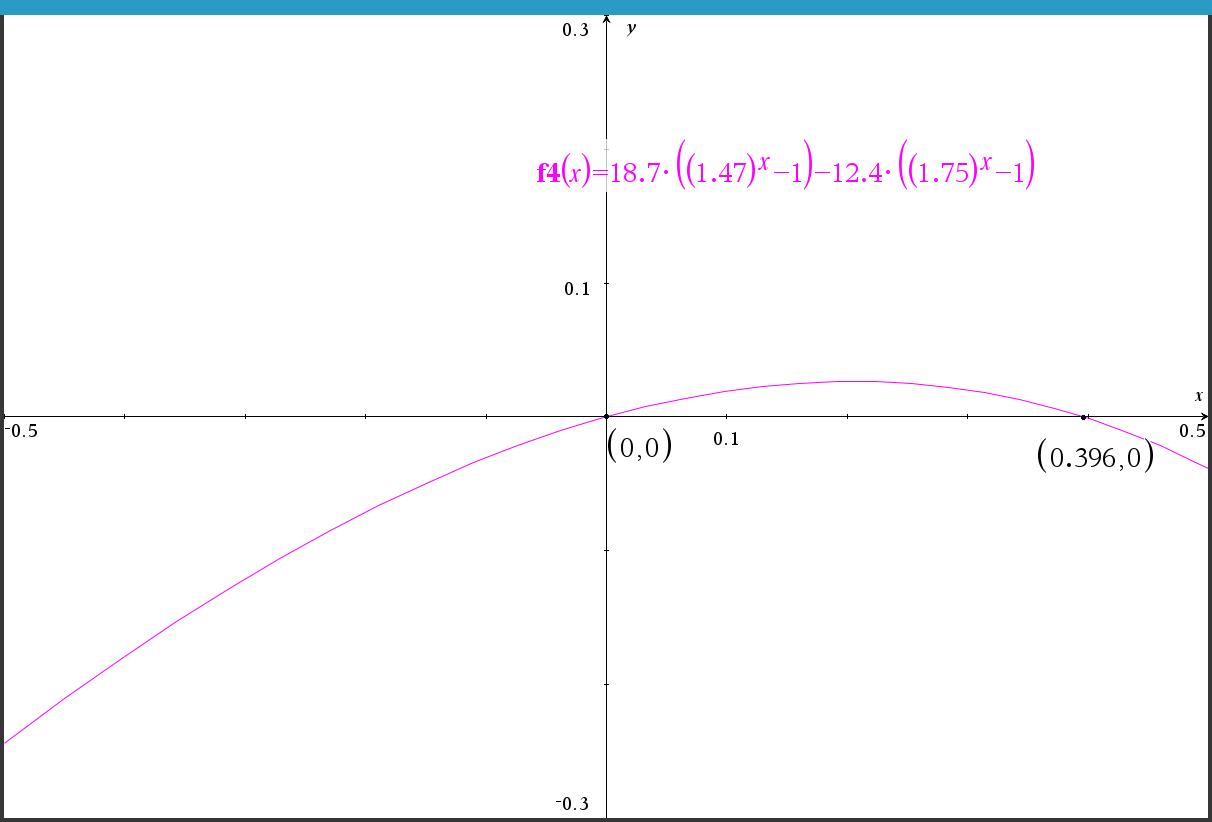
해가 2개 발견되고... solve() 로 답이 안나올만한 건 아닌데... 이상하네요.
-
25
세상의모든계산기 님의 최근 댓글
고장남 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14 낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10