- 세상의 모든 계산기 자유(질문) 게시판 질문 ()
Casio fx-570EX / 991EX, 복소수 모드에서 Stack ERROR 발생하는 원인? (버그 추정)
1. 수식은 0.05+0.4605*log((2)/(0.6*10^(-2))) 입니다.
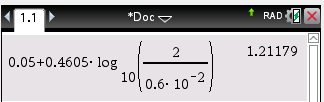
https://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1118&docId=395215225&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=1&search_sort=3&spq=0#
일반 Calculate 모드에서는 이상없이 계산이 잘 됩니다.

2. 그런데 복소수 모드 Complex 에서는 동일하게 입력했을 때
Stack Error 가 나옵니다.

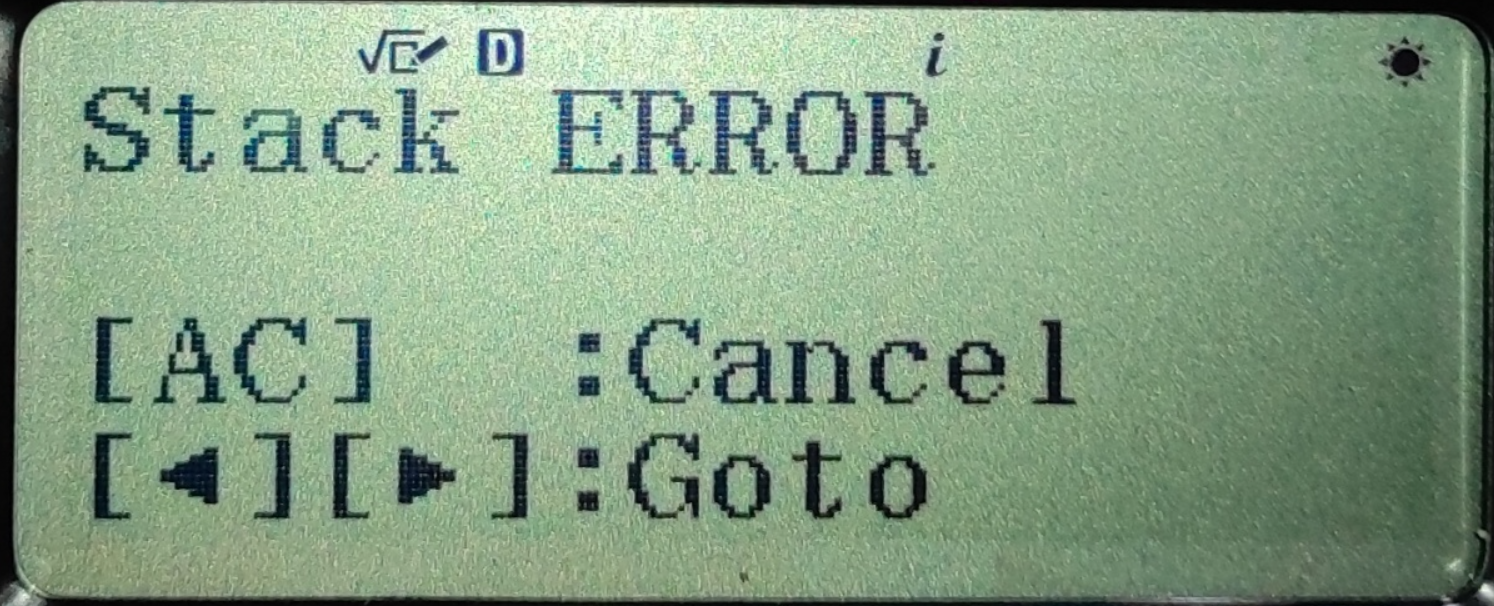
3. Goto 하면 log() 안에 있는 분모의 10^(-2) 로 이동합니다.
분모의 10^-2 를 분자로 보내 10^2 으로 입력하면 에러가 없습니다.
분모의 10^-2 를 【×10x】 버튼을 이용해 분모에 입력하면 에러가 없습니다.
왜 이러는 걸까요? (fx-570ES 에서는 문제 없는 것 같은데 말이죠)
fx-570ES Plus 도 동일한 에러가 발생합니다.
https://kin.naver.com/qna/detail.nhn?d1id=1&dirId=10205&docId=395293601&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=3&search_sort=3&spq=0

댓글4
-
세상의모든계산기
https://gigglehd.com/gg/bbs/902112
링크의 예제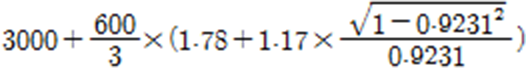
Complex Mode 계산시
fx-570ES PLUS, fx-991EX 모두 Stack ERROR 발생합니다. -
세상의모든계산기
1+(2+(3+(4+(5+(6+6)))))
fx-570ES PLUS, fx-991EX 모두 Stack ERROR 발생합니다.https://www.reddit.com/r/calculators/comments/czohyx/apparent_bug_in_casio_fx991ex_gives_syntax_error/
이상을 종합해 보면...
버그는 아니고, fx-570 급의 Complex 모드의 계산 능력(Stack 공간)이 매우 부실하다는 결론 -
세상의모든계산기
https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=436668037&qb=6rOE7IKw6riw&enc=utf8



세상의모든계산기 님의 최근 댓글
고장남 - POST 진입 실패, 모니터 안나옴 직접 사용할 일이 없어져서, 고향집에 가져다 놓고 어댑터만 꼽아 두었습니다. 마지막으로 켠 것은 25년 6월쯤이 아니었을까 싶습니다. (이상증상은 없었구요) 이번 추석에 가서 켜 보니까, 화면이 아예 안나오더라구요. 집에 가져와서 분해해 살펴보니까 - 어댑터 12V는 정상 - 어댑터 꼽으면 바로 POWER 는 켜집니다. ㄴ POWER ON -> Fan 돌아감 + 파워 LED 들어옴 + NVME에 LED 들어옴 ㄴ HDMI 1, 2 신호 전혀 안들어옴 (모니터 2대 확인) ㄴ 키보드에 LED 안들어옴 (USB 5V 가 안들어오는 듯 함) - 옆구리 버튼은 작동하지 않습니다. 길게 눌러도 꺼지지 않음. 하나씩 제거하면서 변수를 제거해 봤는데, 뭘 해도 상태가 똑같습니다. 보드쪽에 문제가 생긴 것 같습니다. 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14 낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10