- CASIO 570
[fx-570] 행렬 Matrix 의 입력/수정/계산, (역행렬)
-
- 2025.04.20 - 19:08 2015.10.18 - 14:16 19960 1
1. 행렬 모드 MAT
- 행렬은 행렬모드 내에서만 사용 가능합니다.
- 【MODE】 【6】 로 행렬 모드로 진입할 수 있습니다.
- 행렬모드일 때 화면 상단에 MAT 마크가 표시됩니다.
- [fx-570 ES] 시리즈 기종은 최대 3×3 행렬까지 입력 및 계산이 가능하며, 최대 3개의 행렬변수(MatA, MatB, MatC)에 행렬 DATA를 저장하여 계산에 사용합니다.
※ [fx-570 EX] 기종은 4×4 까지 가능합니다.
2. 행렬 관련 함수 및 그 기능
【SHIFT】 【4】 를 눌러서 행렬 관련 기능을 불러냅니다.
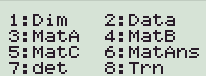
1:Dim 
(차원)을 지정하여 새로운 행렬을 생성
2:Data 
입력되어 있는 행렬의 DATA를 수정
3:MatA ~ 6:MatAns 행렬변수를 불러내서 새로운 계산을 함
7:det 행렬식(Determinant) 을 계산하여 Ans 에 저장
8:Trn 전치행렬(Transpose) 를 구하여 MatAns 에 저장
3. 행렬의 입력 및 연산
행렬의 입력 및 수정
- 다른 모드로 이동하거나 행렬 모드로 재진입하면 DATA가 초기화됩니다. (주의)
- 행렬 요소(Element)의 입력이 끝나면, 【AC】를 눌러 행렬 모드 기본 화면으로 넘어갑니다.
- 행렬은 【SHIFT】【4】 를 눌러 ┌MATRIX┐ 로 진입 후 【2】 DATA 에서 수정합니다.
행렬의 연산
- [fx-570] 기종의 행렬기능은 매우 빈약한 수준입니다. 큰 기대는 하지 않으시는게 좋습니다.
- 행렬끼리의 단순 연산 : 더하기, 빼기, 곱하기(O) / 나누기(X)
- 행렬과 상수의 단순 연산 : 곱하기, 나누기(O) / 더하기, 빼기(X)
- 행렬 DATA를 직접 화면에 띄운 채로 연산할 수는 없고, 행렬이 저장된 행렬변수만을 사용하여 연산할 수 있습니다.
- 행렬의 연산 결과는 Ans가 아닌 MatAns에 저장됩니다.
※ 역행렬(Inverse) 기능은 메뉴에 없고, 행렬변수 호출 뒤, MODE 버튼 아래에 있는 【x-1】버튼을 눌러서 입력합니다.
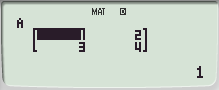
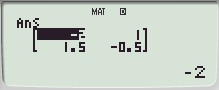
행렬곱은 MatA×MatB 등으로 계산할 수 있습니다.
MatA2 와 MatA3 은 계산이 되지만, MatA^(2) 나 MatA^(3)의 꼴로 입력하면 에러가 발생합니다.
4. 주의 사항
- 행렬 안에 복소수를 입력할 수 없습니다.
- 연립방정식의 해를 구하려는 경우에는 행렬 모드 대신 방정식(EQN) 모드를 이용하는 것이 바람직합니다.
-
25
댓글1
-
세상의모든계산기
역행렬 예제
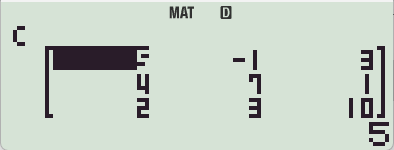-> MatC 에 저장
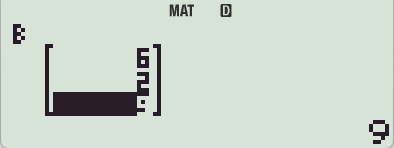-> MatB에 저장MatC(역행렬) * MatB 하면?
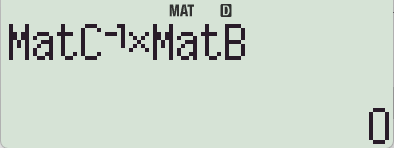
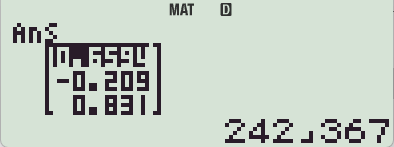
MatC(역행렬만 보면)
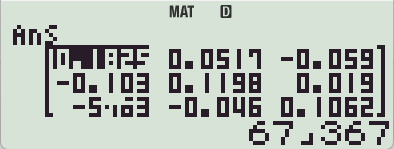
4*4 행렬 -> 역행렬 예제 : fx-570 EX, fx-991 EX
세상의모든계산기 님의 최근 댓글
4*4 행렬 계산이 가능한 fx-570EX 이후 계산기는 행렬 기능을 이용하는 방법도 있지만, 본문 방법이 더 편리한 것 같습니다. [fx-570 EX] 복소수 1차 연립방정식 해 구하기 (feat. MATRIX) https://allcalc.org/21582 2025 10.15 고장남 - POST 진입 실패, 모니터 안나옴 직접 사용할 일이 없어져서, 고향집에 가져다 놓고 어댑터만 꼽아 두었습니다. 마지막으로 켠 것은 25년 6월쯤이 아니었을까 싶습니다. (이상증상은 없었구요) 이번 추석에 가서 켜 보니까, 화면이 아예 안나오더라구요. 집에 가져와서 분해해 살펴보니까 - 어댑터 12V는 정상 - 어댑터 꼽으면 바로 POWER 는 켜집니다. ㄴ POWER ON -> Fan 돌아감 + 파워 LED 들어옴 + NVME에 LED 들어옴 ㄴ HDMI 1, 2 신호 전혀 안들어옴 (모니터 2대 확인) ㄴ 키보드에 LED 안들어옴 (USB 5V 가 안들어오는 듯 함) - 옆구리 버튼은 작동하지 않습니다. 길게 눌러도 꺼지지 않음. 하나씩 제거하면서 변수를 제거해 봤는데, 뭘 해도 상태가 똑같습니다. 보드쪽에 문제가 생긴 것 같습니다. 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14