- TI nspire
[TI-nspire] 행렬의 입력 & 계산 - 확장 라이브러리 Matrix Library
-
- 2024.10.21 - 14:56 2015.01.13 - 22:45 8956 12
1. 라이브러리 설명
행렬의 입력 및 계산을 도와주는 확장 라이브러리입니다.
Matrix pieces Arithmetic function & Cofactor Expansion Program TI-Nspire
By creeras
Ver 1.5 (2024-10-21)
---
Usage
Function_name(matrix1,matrix2,row_number,column_number)
: For overwrite(), add(), subtract(), multiply(), divide()
Dim(matrix1) have to be bigger than dim(matrix2), and have to put all matrix2 elements opon matrix1 elements to calculate it.
Function_name(matrix,row_number,column_number)
: For insert(), insertrow(), insertcol(), minor(), cofactor()
Function_name(matrix,r or c,index)
: For coex()
Function_name(matrix)
: For adjoint(), rank(), lunp()
Caution
Result of Function() is not stored to original matrix. So store it to original matrix variable or new matrix variable.
2. 함수 (및 프로그램) 설명
- add(matrix1,matrix2,row_number,column_number) : 행렬을 일부분만 더함
ㄴ mat_big 행렬에 mat_small을 더함. 4행 2열 ~ 5행 3열 부분만
subtract(matrix1,matrix2,row_number,column_number) : 행렬을 일부분만 뺌
multiply(matrix1,matrix2,row_number,column_number) : 행렬을 일부분만 곱함
divide(matrix1,matrix2,row_number,column_number) : 행렬을 일부분만 나눔 - overwrite(matrix1,matrix2,row_number,column_number) : 행렬을 일부분만 덮어쓰기 ; 기존 값은 무시되고, 새로운 함수의 값이 덧쓰입니다.
- insert(matrix,row_number,column_number) : 행 또는 열을 추가합니다. (0으로 채워져 있음)
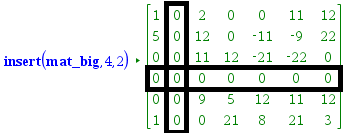
delete(matrix,row_number,column_number) : 행 또는 열을 삭제합니다(=소행렬)
- Insertrow(matrix,row_number,column_number) : 1행(만)의 이동.
ㄴ 나머지 행들간의 순서변화 없음.
ㄴ 내장함수 rowSwap( )은 2행 사이의 위치 교환
Insertcol(matrix,row_number,column_number) : 1열(만)의 이동. (나머지 열들간의 순서변화 없음.)
- minor(matrix,row_number,column_number) : "소행렬식", 부호를 고려하지 않은 소행렬의 행렬식. \( M_{ij} \)
cofactor(matrix,row_number,column_number) : 여인자, 부호를 고려한 소행렬식. \( C_{ij} = (-1)^{i+j} M_{ij} \)
adjoint() : 딸림행렬 = 수반행렬 - lunp() : permutation 없이 LU 분해하는 프로그램. // v1.4에서 추가됨. (다른 것들은 다 함수인데, 이것은 프로그램입니다)
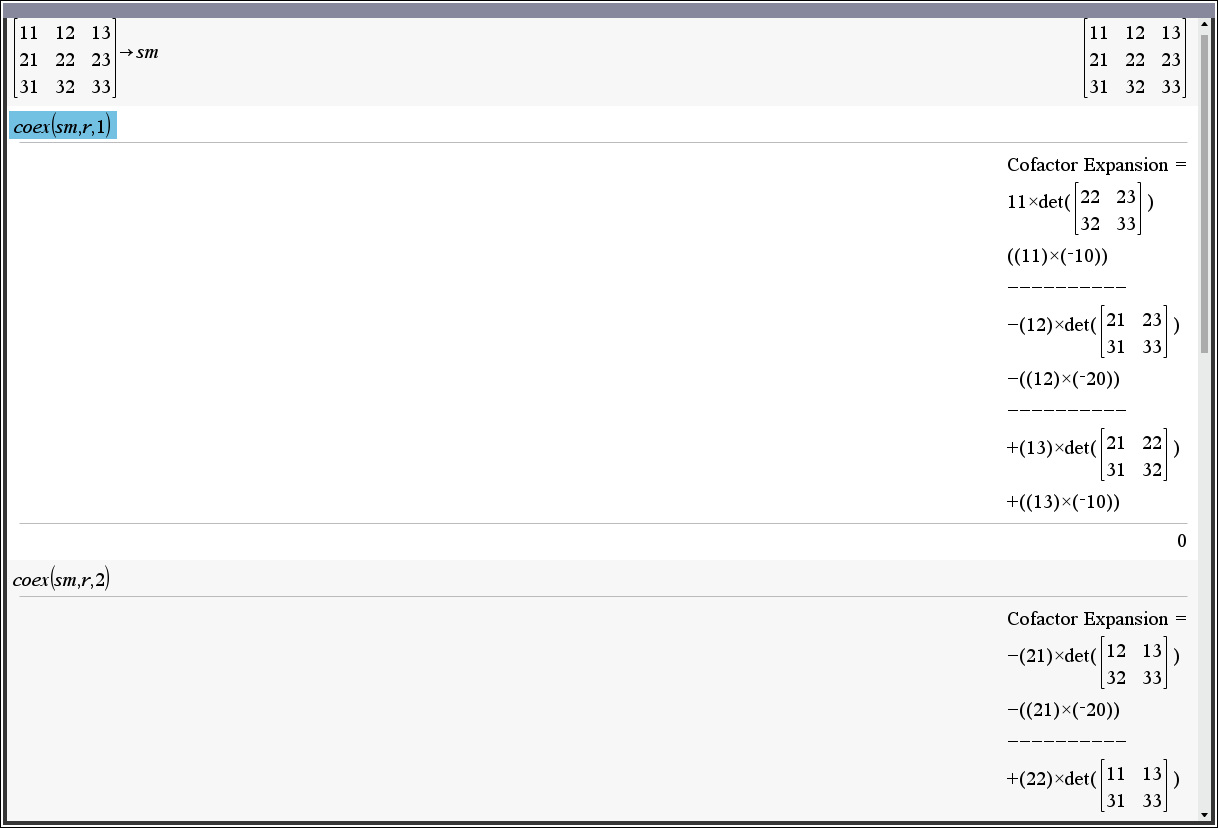
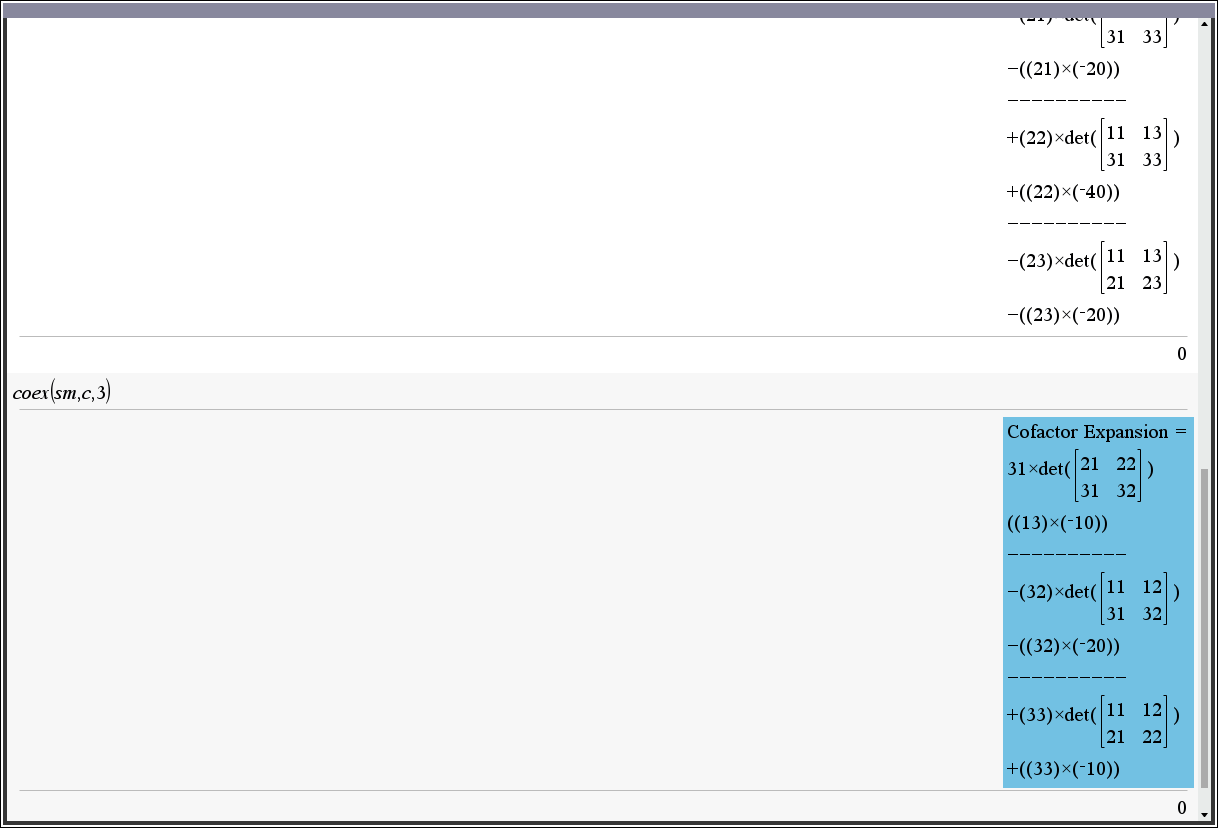
https://allcalc.org/9593#comment_49292 - coex(matrix,r or c,index) : 여인자 전개 // v1.5 에서 수정됨.
3. 사용 방법
3-1. 라이브러리를 다운로드 : matrix.tns
3-2. TI-nspire의 MyLib 폴더에 옮겨 넣고
3-3. refresh Library : 【Doc】 【6】 상세 설명은 다음 링크 확인 https://allcalc.org/35636
사용하시면 됩니다.
4. 동영상 설명
5. 업데이트 내역
V1.31 (2015-11-22)
근사(approx)계산시 rank 오류 해결
V1.40 (2024-10-07)
lunp() 추가 // permutation 없이 LU 분해함.
V1.50 (2024-10-21)
coex() 수정 // 기존에 열선택할 수 없던 문제, 그리고 step-by-step 확인하지 못하던 문제 해결
-
25
댓글12
- 1
- 1
- 2
- 1
- 1
- 2
-
세상의모든계산기
여인자 전개 프로그램 수정 V1.5
Define LibPub coex(mat1,choice,index)= Func :© coex(matrix,r or c,index) :© Initialize :Local mat1_dim,i,j,co.result,minormat,sgn :dim(mat1)→mat1_dim :newMat(mat1_dim[1],2)→co.result : :©Main Body :Disp "Cofactor Expansion =" : :If string(choice)="r" Then : If 1≤index≤mat1_dim[1] Then : For j,1,mat1_dim[2] :[mat1[index,j],cofactor(mat1,index,j)]→co.result[j] : minormat:=delete(mat1,index,j) : sgn:=(−1)^(index+j) : If j=1 Then : If sgn=1 Then : Disp string(mat1[index,j])&"×det(",minormat,")" : Disp "(("&string(mat1[index,j])&")×("&string(minor(mat1,index,j))&"))" : Else : Disp "-("&string(mat1[index,j])&")×det(",minormat,")" : Disp "-"&"(("&string(mat1[index,j])&")×("&string(minor(mat1,index,j))&"))" : EndIf : Else : Disp "----------" : If sgn=1 Then : Disp "+("&string(mat1[index,j])&")×det(",minormat,")" : Disp "+"&"(("&string(mat1[index,j])&")×("&string(minor(mat1,index,j))&"))" : Else : Disp "-("&string(mat1[index,j])&")×det(",minormat,")" : Disp "-"&"(("&string(mat1[index,j])&")×("&string(minor(mat1,index,j))&"))" : EndIf : EndIf : EndFor : Else : Disp "Invalid Row Index" : EndIf : :ElseIf string(choice)="c" Then : If 1≤index≤mat1_dim[2] Then : For i,1,mat1_dim[1] :[mat1[i,index],cofactor(mat1,i,index)]→co.result[i] : minormat:=delete(mat1,i,index) : sgn:=(−1)^(index+i) : : If i=1 Then : If sgn=1 Then : Disp string(mat1[index,i])&"×det(",minormat,")" : Disp "(("&string(mat1[i,index])&")×("&string(minor(mat1,i,index))&"))" : Else : Disp "-("&string(mat1[index,i])&")×det(",minormat,")" : Disp "-"&"(("&string(mat1[index,i])&")×("&string(minor(mat1,index,i))&"))" : EndIf : : Else : Disp "----------" : If sgn=1 Then : Disp "+("&string(mat1[index,i])&")×det(",minormat,")" : Disp "+"&"(("&string(mat1[index,i])&")×("&string(minor(mat1,index,i))&"))" : Else : Disp "-("&string(mat1[index,i])&")×det(",minormat,")" : Disp "-"&"(("&string(mat1[index,i])&")×("&string(minor(mat1,index,i))&"))" : EndIf : : EndIf : EndFor : Else : Disp "Invalid Column Index" : EndIf :Else : Disp "Invalid Choice : Input ""r"" or ""c"" for 2nd argument" :EndIf : :© Finalize :Return det(mat1) :EndFunc사용 예시
세상의모든계산기 님의 최근 댓글
500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28 ChatGPT-5 💯 네, 정확히 그 지점을 짚으셨어요. 요약하면 이렇게 말할 수 있습니다: “생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다. 즉, 문자에서는 더 강하게 결합, 숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다. 🔹 두 경우의 구조적 차이 식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용 🔹 왜 문자식은 결합력이 더 강한가? 기호적 표현의 안정성 (ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다. 그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다. ab ÷ ab = (ab) ÷ (ab) 함수 표기와 구분 필요 예: (sinx ÷ x) 에서 sinx는 sin(x)로 묶여야 의미가 있습니다. 이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다. 🔹 반면 숫자·괄호에서는 (3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고, 여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다. 따라서 27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81 처럼 좌→우 순서로 처리합니다. 🔹 결론 생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다. 문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식) 숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산) 이건 “규칙이 바뀐 것”이 아니라, 표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. 2025 10.28