- 세상의 모든 계산기 수학, 과학, 공학 이야기 공학 ()
음압레벨(SPL), Peak, RMS 관계식
문제

풀이
음압레벨(Sound Pressure Level, SPL)을 dB로 표현할 때, 다음 공식을 사용합니다:
\[
SPL = 20 \log_{10} \left(\frac{P_{RMS}}{P_0}\right)
\]
여기서:
- \( P_{RMS} \)는 RMS(최대 평균 제곱근) 음압값 (Pa)
- \( P_0 \)는 기준 음압, 보통 20 μPa (또는 \( 2 \times 10^{-5} \) Pa)
문제에서 SPL이 130 dB이고, 기준 음압 \( P_0 = 2 \times 10^{-5} \) Pa입니다.
이를 이용하여 \( P_{RMS} \) 값을 계산하고, 그 후에 피크 값( \( P_{Peak} \) )을 구할 수 있습니다.
1. RMS 음압 \( P_{RMS} \) 계산:
\[
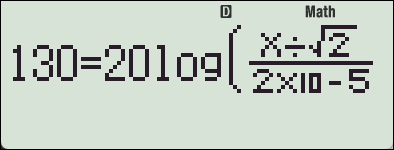
130 = 20 \log_{10} \left(\frac{P_{RMS}}{2 \times 10^{-5}}\right)
\]
양변을 20으로 나눕니다:
\[
\frac{130}{20} = \log_{10} \left(\frac{P_{RMS}}{2 \times 10^{-5}}\right)
\]
\[
6.5 = \log_{10} \left(\frac{P_{RMS}}{2 \times 10^{-5}}\right)
\]
지수 형태로 변환하면:
\[
10^{6.5} = \frac{P_{RMS}}{2 \times 10^{-5}}
\]
따라서,
\[
P_{RMS} = 10^{6.5} \times 2 \times 10^{-5} = 2 \times 10^{1.5}
\]
2. \( P_{RMS} \) 계산 후 피크 값 구하기:
RMS 값에서 피크 값을 구하는 과정에서는 보통 다음의 관계를 사용합니다:
\[
P_{Peak} = \sqrt{2} \times P_{RMS}
\]
따라서, 위 계산을 통해 구한 \( P_{RMS} \) 값을 사용하여 피크 값을 구합니다.
\[
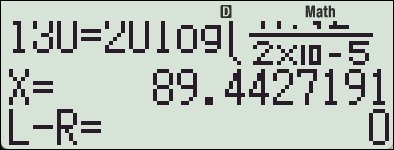
P_{Peak} = \sqrt{2} \times 2 \times 10^{1.5} \text{ Pa} \approx 89.443 \text{ Pa}
\]
따라서, Peak 값은 약 89.443 Pa 입니다.
계산기 fx-570 ES 이용시 (한번에 계산)








세상의모든계산기 님의 최근 댓글
낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10 마지막 발언이 마지막 힌트이자 문제의 핵심이군요. 처음 들은 달이 8월이었다면 (15일인지 17일인지 확신할 수 없어서) 마지막 대사를 할 수 없지만, 처음 들은 달이 7월이었다면 (선택지가 16일 하나라서 확신이 가능하므로) 마지막 대사를 할 수 있다. 대사를 했으니 7월이다. 이제 이해되었습니다. 지금 보니까 이해가 되는데, 당시에는 왜 이해가 안됐을까요? 세가지 전제 하에 문제를 풀면 A는 마지막 대화 2줄만으로 C의 생일을 알 수 없어야 정상인데, 무슨 이유에서인지 "그럼 나도 앎!"이라고 선언해 버립니다. 알게 된 이유를 대화 속에서 찾을 수는 없습니다. 이 편견에 사로잡혀 빠져나오지 못하고 다른 길로 계속 샜나봅니다. 2025 10.09 (장*훈)님 (+10,000원) 계좌 후원(2025/10/09) 감사 드립니다. 2025 10.09 원래 식이 풀어진 상태에서는 두번째 인수 v가 분모, 분자에 섞여 있어서 계산기가 처리하지 못하는 듯 합니다. 이 때는 위에서와 반대로 분모 부분만 다른 문자(w)로 치환한 다음 completesquare(,v^2) 처리를 하면 일부분은 묶이는 듯 합니다. 하지만 여기서 처음 모양으로 더 이상 진행되진 않네요. 2025 10.08 전체 식에서 일부분(분모, 루트 내부)만 적용할 수는 없습니다. 번거롭더라도 해당 부분만 따로 끄집어 내서 적용하셔야 합니다. https://allcalc.org/30694#comment_30704 2025 10.08