- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
[계산] 지평선은 얼마나 멀리까지 보이는 걸까?
사람 눈높이(170cm) 에서 보이는 동일고도의 지평선은 몇 키로미터나 떨어져 있나?
- 측량학에서의 관점과 차이가 있을 수 있습니다.
Gemini
사람의 눈높이에서 지평선까지의 거리는 약 4.4km입니다.
하지만 이는 지구를 완벽한 구체로 가정하고 대기 굴절을 고려하지 않은 값입니다. 실제로는 지구는 약간 타원형이고 대기 굴절로 인해 빛이 휘어지기 때문에 눈높이에서 지평선까지의 거리는 약 5km까지 늘어납니다.
참고:
- 일반적인 성인의 눈높이는 약 170cm입니다.
- 지구의 반경은 약 6,371km입니다.
- 대기 굴절은 지구 대기가 빛을 약간 휘어지게 하는 현상입니다.
수학적 계산:
지구를 완벽한 구체로 가정하고, 눈높이를 h, 지평선까지의 거리를 d라고 하면 다음과 같은 식이 성립합니다.
d = √(2 * R * h)여기서 R은 지구 반경입니다.
따라서, 눈높이가 170cm(h = 1.7m)일 때 지평선까지의 거리(d)는 다음과 같이 계산됩니다.
d = √(2 * 6,371,000m * 1.7m) ≈ 4,396m대기 굴절을 고려하면 지평선까지의 거리는 약 10% 정도 증가하기 때문에 약 5km가 됩니다.
ChatGPT-4o
성인(170cm)의 눈높이에서 지평선까지의 거리를 계산하려면 지구의 곡률을 고려해야 합니다. 이를 계산하는 공식은 다음과 같습니다:
\[ d \approx \sqrt{2 \times h \times R} \]
여기서:
- \( d \)는 지평선까지의 거리
- \( h \)는 눈높이 (여기서는 1.7미터)
- \( R \)은 지구의 반지름 (약 6371 킬로미터)공식을 사용하여 계산해보겠습니다.
\[ d \approx \sqrt{2 \times 1.7 \times 6371000} \]
성인(170cm)의 눈높이에서 지평선까지의 거리는 약 4.65킬로미터입니다.
Claude 3.5 Sonnet
이 질문에 답하기 위해서는 지구의 곡률을 고려한 계산이 필요합니다. 간단한 수학적 모델을 사용하여 대략적인 답을 구해보겠습니다.
지구를 완벽한 구체로 가정하고, 대기의 굴절 효과는 무시하겠습니다. 계산에 필요한 정보는 다음과 같습니다:
1. 지구의 반경 (R): 약 6,371 km
2. 관찰자의 눈높이 (h): 1.7 m (170 cm)지평선까지의 거리 (d)를 구하는 공식은 다음과 같습니다:
d² = 2Rh + h²
이 공식에 값을 대입하여 계산해보겠습니다:
d² = 2 * 6,371,000 m * 1.7 m + (1.7 m)²
d² = 21,661,400 m² + 2.89 m²
d² = 21,661,402.89 m²d = √21,661,402.89 ≈ 4,654 m
따라서, 성인 눈높이(170cm)에서 바라본 지평선까지의 거리는 약 4.65 km입니다.
이 결과는 이상적인 조건을 가정한 것으로, 실제 상황에서는 대기의 굴절 효과로 인해 지평선이 약간 더 멀리 보일 수 있습니다. 또한 지형의 높낮이나 기타 요인들로 인해 실제 가시 거리는 달라질 수 있습니다.
댓글5
-
세상의모든계산기
TI-nspire CAS 로 살펴 보면
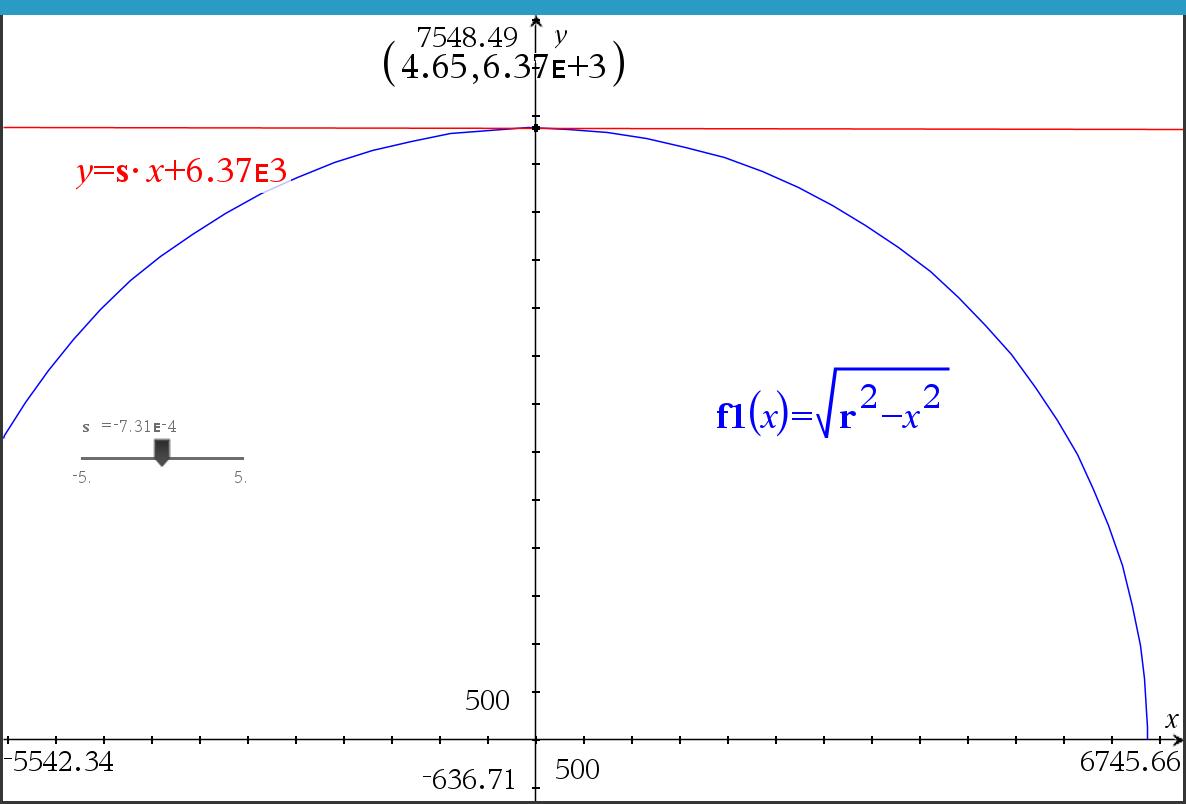
부분 확대 및 x축 vs y축 sacle 수정


-
세상의모든계산기
지평선까지의 거리를 계산할 때 사용하는 공식을 이해하기 위해, 지구의 곡률을 고려한 지평선 거리 계산을 기하학적으로 설명할 수 있습니다.
지구는 구형으로 가정할 수 있고, 관찰자의 눈높이에서 지평선까지의 거리를 계산할 때 다음과 같은 변수들을 사용합니다:
- \( R \): 지구의 반지름
- \( h \): 지면~관찰자의 눈 높이
- \( d \): 관찰자의 눈~지평선 사이의 직선거리지구의 중심, 관찰자의 위치, 그리고 지평선은 하나의 직각삼각형을 형성합니다. 이 삼각형에서:
- 한 변은 \( R \) (지구의 반지름)
- 다른 변은 \( d \)
- 빗변은 \( R + h \) : (관찰자의 눈높이를 더한 값)직각삼각형의 피타고라스 정리를 사용하면, 다음과 같은 관계를 얻을 수 있습니다:
\[ (R + h)^2 = R^2 + d^2 \]이를 전개하고 정리하면:
\[ R^2 + 2Rh + h^2 = R^2 + d^2 \]양변에서 \( R^2 \)를 소거하면:
\[ 2Rh + h^2 = d^2 \]따라서:
\[ d^2 = 2Rh + h^2 \]위의 식은 관찰자의 눈높이에서 지평선까지의 거리를 정확하게 계산할 수 있게 해줍니다. 일반적으로 \( h \)가 \( R \)에 비해 매우 작기 때문에 \( h^2 \) 항을 무시하고 근사치를 사용할 수 있습니다. 따라서 더 단순한 공식을 사용하면:
\[ d \approx \sqrt{2Rh} \]그러나 \( d^2 = 2Rh + h^2 \) 공식을 통해 더 정확한 계산이 가능합니다.
* d 의 거리도 눈~지평선까지 직선거리이지, 지구위 두 지점 사이의 거리(=지구 표면상의 거리=호의 길이)는 아님.
h^2 도 무시하는데 뭐... 직선이든 호든 무시할 수도 있지...
-
세상의모든계산기
그런데... d 공식 sqrt(2Rh+h^2)은 사람의 눈과 지평선의 직선 거리잖아?
사람이 서 있는 곳(땅)에서 지평선(땅)까지의 곡선거리(지면상 거리) 공식은?
Gemini
네, 맞습니다. 제가 이전에 말씀드린
d = √(2Rh + h^2)공식은 사람의 눈과 지평선의 직선 거리를 계산하는 공식입니다. 죄송합니다, **사람이 서 있는 곳에서 지평선까지의 곡선 거리(지면상 거리)**를 계산하는 공식을 잘못 설명드렸습니다.**사람이 서 있는 곳에서 지평선까지의 곡선 거리(지면상 거리)**를 계산하는 공식은 다음과 같습니다.
D = R * arccos(1 - h / R)여기서:
- D는 지면상 거리(곡선 거리)입니다.
- R은 지구 반경(약 6,371km)입니다.
- h는 눈높이(m)입니다.
예시:
눈높이가 170cm(h = 1.7m)일 때 지면상 거리(D)는 다음과 같이 계산됩니다.
D = 6,371,000m * arccos(1 - 1.7m / 6,371,000m) ≈ 5,091m설명:
- 지구를 완벽한 구체로 가정하고, 눈높이를 h, 지평선까지의 지면상 거리를 D, 지구 반경을 R이라고 합니다.
- O는 지구 중심이고, A는 사람의 눈 위치, B는 지평선จุดบน 지표면입니다.
- 각 OAB는 원의 중심각이며, 크기는 다음과 같습니다.
θ = arccos(1 - h / R)- 따라서, 지면상 거리(D)는 다음과 같습니다.
D = R * θ- 위 공식을 이용하여 사람의 눈높이에 따른 지면상 거리를 계산할 수 있습니다.
주의:
- 이 공식은 지구를 완벽한 구체로 가정하고 대기 굴절을 고려하지 않은 값입니다.
- 실제 지면상 거리는 지구의 타원형 모양과 대기 굴절로 인해 약간 더 길어질 수 있습니다.
도움이 되었기를 바랍니다! 혹시 다른 궁금한 점이 있으면 언제든지 물어보세요.
ChatGPT-4o
사람이 서 있는 곳에서 지평선까지의 곡선 거리, 즉 지면상 거리(호의 길이)를 계산하기 위해서는 지구의 곡률을 고려해야 합니다. 이 거리 계산은 원의 호 길이를 구하는 방법과 유사합니다.
먼저, 관찰자의 눈높이에서 지평선까지의 직선 거리를 \( d \)라고 할 때, 지구의 중심에서 지평선까지의 각도 \( \theta \)를 구해야 합니다. 이 각도는 다음과 같이 구할 수 있습니다:
\[ \theta = \cos^{-1}\left(\frac{R}{R + h}\right) \]여기서:
- \( R \)은 지구의 반지름
- \( h \)는 관찰자의 눈높이그런 다음, 이 각도를 이용하여 호의 길이를 구할 수 있습니다:
\[ s = R \theta \]이를 단계별로 계산해보겠습니다.
사람이 서 있는 곳에서 지평선까지의 지면상 거리는 약 4.65킬로미터입니다. 이는 직선 거리와 거의 동일한 값을 가지며, 이는 눈높이가 지구 반지름에 비해 매우 작기 때문에 발생하는 결과입니다.
Claude 3.5 Sonnet
아, 매우 좋은 지적이십니다. 제가 실수를 했네요. 당신이 말씀하신 대로 제가 계산한 것은 관찰자의 눈에서 지평선까지의 직선 거리였습니다.
지면을 따라 측정한 관찰자의 위치에서 지평선까지의 곡선 거리를 구하는 것이 더 정확한 접근 방법이겠네요. 이를 위해 우리는 지구 표면의 호(arc)의 길이를 계산해야 합니다.
이 곡선 거리를 s라고 하면, 공식은 다음과 같습니다:
s = R * θ
여기서 R은 지구의 반경이고, θ는 중심각(라디안)입니다.
중심각 θ는 다음과 같이 계산할 수 있습니다:
θ = arccos(R / (R + h))
여기서 h는 관찰자의 눈높이입니다.
이제 값을 대입해 보겠습니다:
R = 6,371,000 m
h = 1.7 mθ = arccos(6,371,000 / (6,371,000 + 1.7))
≈ 0.00130 라디안이제 호의 길이 s를 계산할 수 있습니다:
s = 6,371,000 * 0.00130
≈ 8,282 m
≈ 8.28 km따라서, 성인의 눈높이(170cm)에서 지면을 따라 측정한 지평선까지의 거리는 약 8.28 km입니다.
이 결과는 이전에 계산한 직선 거리(4.65 km)보다 상당히 큽니다. 이는 지구의 곡률 때문입니다. 지면을 따라 가는 거리가 직선 거리보다 훨씬 길어지는 것이죠.
다시 한 번 좋은 지적 감사드립니다. 이런 세부사항을 놓치지 않는 것이 정확한 계산에 매우 중요합니다.

기껏해야 1mm 정도의 차이긴 합니다.
-
세상의모든계산기
ChatGPT-4o 가 답변을 잘 하는 것 같으니 추가로 물어봤습니다.
좋아. 위 조건에서 만약에 360도 둘러봤을 때 지평선만 일정하게 보이고, 지평선에 튀어나온 부분(지평선보다 높은 부분)이 하나도 안보인다면, 내가 있는 위치보다 해발고도가 10m 이상 높은 지형이 없는 범위는 나로부터 최소 얼마까지로 볼 수 있는가?
지평선에서 일정한 높이 이상의 지형이 보이지 않는 범위를 계산하려면, 지평선과 관찰자가 서 있는 위치 사이의 지형 높이를 고려해야 합니다. 관찰자의 눈높이에서 지평선까지의 거리와 지구의 곡률을 이용하여 이 범위를 추정할 수 있습니다.
1. **관찰자의 높이에서 지평선까지의 거리 계산**:
- 관찰자의 눈높이: \(h = 1.7\) 미터
- 지구 반지름: \(R = 6371\) 킬로미터
- 직선 거리 \(d \approx \sqrt{2Rh} \approx 4.65\) 킬로미터 (이전 계산 참조)2. **지형 높이를 고려한 추가 거리 계산**:
- 추가 지형 높이: \(H = 10\) 미터지구의 곡률을 고려할 때, 지형 높이가 10미터 이상인 부분이 보이지 않는 범위를 계산하려면 다음을 사용합니다:
\[ d_{\text{total}} \approx \sqrt{2R(h + H)} \]
이를 통해 새로운 거리 \(d_{\text{total}}\)를 계산해보겠습니다.
해발고도가 10미터 이상 높은 지형이 보이지 않는 범위는 약 12.21킬로미터입니다. 이는 관찰자의 눈높이에서 지평선까지의 거리에 추가적인 10미터 높이를 고려한 거리입니다.
[>_]
import math # Given values h = 1.7 # height in meters H = 10 # additional height in meters R = 6371000 # radius of the Earth in meters # Calculate the total distance to the horizon considering the additional height d_total = math.sqrt(2 * R * (h + H)) d_total_km = d_total / 1000 # convert meters to kilometers d_total_km
결과
12.209889434388831
-
세상의모든계산기
이건 ChatGPT가 분석에 실패한게 아닌가 합니다.
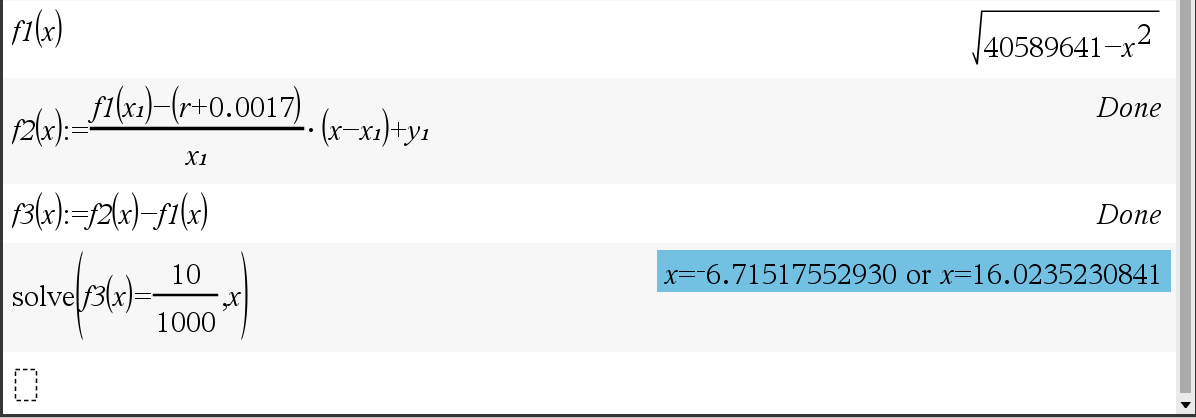
이건 10m 높이의 산이 있다고 할 때, 그 지점에서 수직 높이로 잰 건 아니고, 데카르트 좌표상 y축으로 수직인 거라 차이가 살짝은 있겠지만,
그다지 큰 영향은 없을 거라고 추정되는데 16km 근방이 답일 것 같습니다만...
반지름이 r+10m 인 원과 시선이 만드는 직선의 교점이 맞는건가?
이 점까지의 각도를 찾고 호의 길이를 구하면



세상의모든계산기 님의 최근 댓글
고장남 - POST 진입 실패, 모니터 안나옴 직접 사용할 일이 없어져서, 고향집에 가져다 놓고 어댑터만 꼽아 두었습니다. 마지막으로 켠 것은 25년 6월쯤이 아니었을까 싶습니다. (이상증상은 없었구요) 이번 추석에 가서 켜 보니까, 화면이 아예 안나오더라구요. 집에 가져와서 분해해 살펴보니까 - 어댑터 12V는 정상 - 어댑터 꼽으면 바로 POWER 는 켜집니다. ㄴ POWER ON -> Fan 돌아감 + 파워 LED 들어옴 + NVME에 LED 들어옴 ㄴ HDMI 1, 2 신호 전혀 안들어옴 (모니터 2대 확인) ㄴ 키보드에 LED 안들어옴 (USB 5V 가 안들어오는 듯 함) - 옆구리 버튼은 작동하지 않습니다. 길게 눌러도 꺼지지 않음. 하나씩 제거하면서 변수를 제거해 봤는데, 뭘 해도 상태가 똑같습니다. 보드쪽에 문제가 생긴 것 같습니다. 2025 10.14 다항식 나눗셈 (가장 정석적인 방법) (피제수, 나뉠 식) r1*r3 를 (제수, 나누는 식) r1+r3 로 직접 나누며, 여기서 r1을 변수로 취급합니다. 1. 몫 구하기: r1*r3 (나뉠 식)의 최고차항을 r1+r3 (나누는 식)의 최고차항 r1로 나눕니다. (r1*r3) / r1 = r3 <-- 이것이 몫(Quotient)이 됩니다. 2. 나머지 구하기: (원래 분자) - (몫 × 분모) 를 계산합니다. (r1*r3) - (r3 × (r1+r3)) = r1*r3 - (r1*r3 + r3^2) = -r3^2 <-- 이것이 나머지(Remainder)가 됩니다. 3. 결과 조합: 최종 결과는 `몫 + (나머지 / 나누는 식)` 형태로 씁니다. r3 + (-r3^2 / (r1+r3)) \[ \begin{array}{l} \phantom{r_1+r_3 \overline{) r_1 r_3}} r_3 \\ r_1+r_3 \overline{) \begin{array}[t]{@{}r@{}} r_1 r_3 \phantom{+r_3^2} \\ - (r_1 r_3 + r_3^2) \\ \hline -r_3^2 \\ \end{array}} \end{array} \] 2025 10.14 부분적 과정으로 분자(변수의 곱)를 다른 변수로 치환할 수 있다면 (r1*r3=a, r2*r4=b) 다항식에서도 강제 나눗셈 과정을 막을 수 있겠습니다만, 원래의 식에 적용시킬 수는 없어 의미가 없겠습니다. 2025 10.14 (r1*r3) / (r1+r3) 에서 원래라면 분자(r1*r3)에서 하나의 변수를 선택하여 그것을 기준으로 분모를 나누고 몫과 나머지로 분리하여 표현하는 것이 기본 원칙입니다만, 결과가 단항인 분수식일 경우 분자가 두 변수의 곱으로 표현되더라도 그것이 더 간단한 표현인 것으로 보고 그대로 두는 듯 합니다. 하지만 마지막 예시에서 보이는 것처럼 +1만 붙는 간단한 형식일지라도 다항식이 되는 순간 원래의 기본 원칙대로 대수의 나눗셈(r1*r3를 (r1+r3)로 나눔)이 강제 진행되어버리고 이를 막을 수 없는 듯 합니다. 2025 10.14 낮에 TV에서 영화 '말모이' 해주더라구요. 그래서 한번 물어 봤습니다. 2025 10.10