역삼각함수 (inverse trigonometric function)
-
- 2024.07.20 - 14:16 2015.02.27 - 19:07 38405 12
1. 역삼각함수란?
역삼각함수(inverse trigonometric function)는 삼각함수의 역함수를 말한다.
2. 역삼각함수의 특징
삼각함수는 단사함수가 아니기 때문에 이의 역함수를 정의하려면 정의역과 치역을 제한하는 것이 필요하다.
아래는 역삼각함수들의 정의와 표기법, 정의역과 치역들을 나타낸 표이다.
| 이름 | 표기법 | 정의 | 정의역 | 치역 |
|---|---|---|---|---|
| 아크사인 | y = arcsin x 또는 y = sin-1 x | x = sin y | −1부터 +1 | −π/2 ≤ y ≤ π/2 |
| 아크코사인 | y = arccos x 또는 y = cos-1 x | x = cos y | −1부터 +1 | 0 ≤ y ≤ π |
| 아크탄젠트 | y = arctan x 또는 y = tan-1 x | x = tan y | 모든 실수 | −π/2 < y < π/2 |
| 아크코탄젠트 | y = arccot x 또는 y = cot-1 x | x = cot y | 모든 실수 | 0 < y < π |
| 아크시컨트 | y = arcsec x 또는 y = sec-1 x | x = sec y | −∞부터 −1과 1부터 ∞ | 0 ≤ y < π/2 or π/2 < y ≤ π |
| 아크코시컨트 | y = arccsc x 또는 y = csc-1 x | x = csc y | −∞부터 −1과 1부터 ∞ | −π/2 ≤ y < 0 or 0 < y ≤ π/2 |
정의역을 복소수로 두게되면 위에서 치역의 범위는 실수부의 범위가 된다.
출처 : http://ko.wikipedia.org/wiki/역삼각함수
영문판 : https://en.wikipedia.org/wiki/Inverse_trigonometric_functions
3. 주의 사항
- y = sin-1 x 의 -1을 를 지수로 해석해서, 곱하기 역수인 y = {sin(x)}-1 = (1 ÷ ((sin(x))) 로 계산하면 안된다.
- 삼각함수 및 역삼각함수를 손으로 정확하게 구하는 방법은 없다. 따라서 삼각함수표나 공학용 계산기를 이용해야만 한다.
(특수한 경우 테일러 급수 등을 이용해 근사값을 빠르게 구하는 방법은 있습니다만...
참고 : http://jjycjnmath.tistory.com/32 ) - 역삼각함수의 치역 범위(=결과값의 범위)를 잘 따져야 한다.
-
25
댓글12
-
세상의모든계산기
키 입력 방법
역삼각함수는 대부분의 공학용 계산기에 기본으로 내장되어 있습니다.
컴퓨터에서 쌍시옷 누르려면 【SHIFT】+【ㅅ】 누르는 것처럼 키의 조합으로 입력할 수 있습니다.
다만, 【SHIFT】에 해당하는 키를 누른 채로 유지할 필요는 없고, 순서대로만 누르시면 됩니다.
ArcSin
ArcCos
ArcTanSHIFT 에 해당하는 버튼은 보통 좌측 최상단에 위치하고 있고, 계산기마다 이름이 다른데 【SHIFT】, 【2nd F】, 【Ctrl】등으로 사용합니다.
-
세상의모든계산기
삼각함수표
( 출처 : http://netp.tistory.com/6)
-
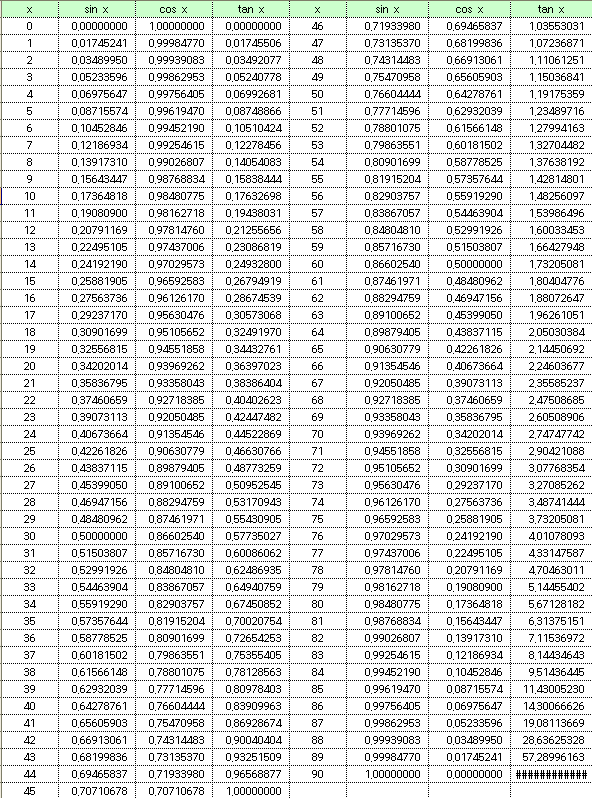
세상의모든계산기
윈도우 공학용 계산기
버튼을 누르면 역삼각함수가 나옵니다.
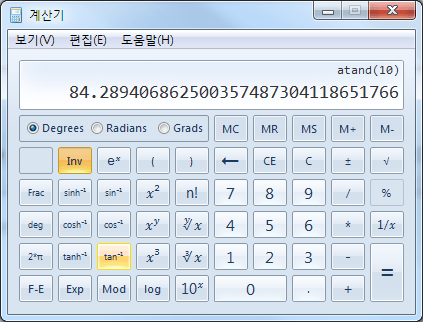
ex) arctan(10) 의 계산
-
세상의모든계산기
울프람 알파(Web)
http://www.wolframalpha.com/input/?i=arccos%280.8615%29
-
세상의모든계산기
각도 설정
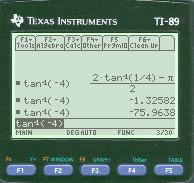
역삼각함수는 출력 결과값이 각도 단위이기 때문에,
계산기의 Setting - Angle(각도) 사전 설정값에 따라 결과가 radian / degree 로 선택되어 출력됩니다.
http://www.allcalc.org/4217 -
세상의모든계산기2016.03.07 - 23:26 #15666Knowledge Base
Home > Product Usage > TI-73 Explorer™ Family > > Solution 11693
Solution 11693: Algorithm for Solving Trigonometric Functions (Sine, Cosine and Tangent) on Texas Instruments' Graphing Calculators.
Type Question and Answer
Last Updated 07-DEC-2007 09:01:14
How does TI graphing calculators compute values for sine, cosine and tangent?
Texas Instruments uses the CORDIC algorithm method to compute trigonometric and other transcendental functions. A recent thread on Graph-TI asks about the internal methods used to compute trigonometric and other transcendental functions.
Most practical algorithms in use for transcendental functions are either polynomial approximations or the CORDIC method. TI calculators have almost always used CORDIC, the exceptions being the CC-40, TI-74 and TI-95 which used polynomial approximations.
In the PC world, the popular Intel math co-processors like the 8087 use CORDIC methods, while the Cyrix 83D87 uses polynomial methods. There are pros and cons to both methods. References 1 and 2 give some information on these devices but not down to the detailed algorithm level.
The polynomial approximations, however, are not usually familiar ones like a Taylor's series, but more related to Chebyshev polynomials. Early work on this topic was done by Hastings (ref 3) which is a fascinating book that represents a lot of tedious work in an age when "computers" were still likely to be people!
A more recent standard reference for constructing these polynomials is Hart (ref 4). A thorough treatment of the minor details one has to deal with in implementing the full algorithms for elementary functions (like binary versus decimal number representations and ranging for general arguments) is in Cody(ref 5).
The CORDIC algorithm is a super example of an approach that is quite different from traditional math and which is very efficient. One often sees a very specialized problem solution like this in many areas of engineering and science, which makes exposure to ideas of this type valuable in education, at least for advanced students.
CORDIC is an acronym for COrdinate Rotation DIgital Computer and was developed by J.E. Volder in 1959 (ref 6). Additional articles and one book chapter covering the technique are given in references 7 - 10. All these articles are complete enough to give the essentials of the method but each one reveals interesting variations. To give you a flavor for the idea and some material to work with without tracking down these references, we will give a worked example and a general description of the principle.
The concept of CORDIC is to take an angle theta and "rotate" a vector over this angle towards zero in a series of steps such that the sum of all the steps taken equals theta and we can accumulate corresponding X and Y increments for each step such that when we complete the process, Y/X = tan(theta). Variations of this basic concept can result in all the forward and inverse trigs as well as square root, hyperbolic trigs, and the exponential and logarithm functions.
Please see the graphing calculator guidebooks for more information and examples on using the sine, cosine and tangent functions. -
세상의모든계산기
atan2(y,x)
atan() 함수의 치역이 -pi/2 ~ pi/2 이기 때문에, 이 결과만으로는 좌표평면상 두 점의 위치관계를 정확하게 알기 어렵다.
이를 해결하기 위해 atan2(y,x) 가 필요함. 이 함수의 치역은 -pi ~ pi 로 정확한 방향을 특정할 수 있다.https://en.wikipedia.org/wiki/Atan2
https://www.medcalc.org/manual/atan2_function.php
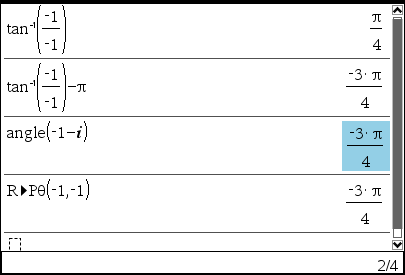
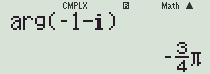
복소수 취급이 불가능한 계산기는 arg() 함수가 없습니다. 대신 pol(x,y) 함수를 이용해 각도값을 찾을 수 있습니다.
세상의모든계산기 님의 최근 댓글
3×3 이상인 행렬의 행렬식 determinant https://allcalc.org/50536 2025 12.30 답에 이상한 숫자 14.2857142857가 들어간 것은 조건식에 소숫점(.) 이 들어가 있기 때문에 발생한 현상이구요. 100÷7 = 14.285714285714285714285714285714 소숫점 없이 분수로 식이 주어졌을 때와 결과적으로는 동일합니다. 2025 12.30 그럼 해가 무한히 많은지 아닌지 어떻게 아느냐? 고등학교 수학 교과과정에 나오는 행렬의 판별식(d, determinant)을 이용하면 알 수 있습니다. ㄴ 고교과정에서는 2x2 행렬만 다루던가요? 연립방정식의 계수들로 행렬을 만들고 그 행렬식(determinant)을 계산하여야 합니다. 행렬식이 d≠0 이면 유일한 해가 존재하고, d=0 이면 해가 없거나 무수히 많습니다. * 정상적인 경우 (`2y + 8z = 115`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 8 | 행렬식 값 = 1(0 - (-7)) - 1(8 - 0) = 7 - 8 = -1 (0이 아니므로 유일한 해 존재) * 문제가 된 경우 (`2y + 7z = 100`)의 계수 행렬: 1 | 1 1 0 | 2 | 1 0 -3.5 | 3 | 0 2 7 | 행렬식 값 = 1(0 - (-7)) - 1(7 - 0) = 7 - 7 = 0 (0이므로 유일한 해가 존재하지 않음) 2025 12.30 좀 더 수학적으로 말씀드리면 (AI Gemini 참고) 수학적 핵심 원리: 선형 독립성(Linear Independence) 3원 1차 연립방정식에서 미지수 x, y, z에 대한 단 하나의 해(a unique solution)가 존재하기 위한 필수 조건은 '주어진 세 개의 방정식이 서로 선형 독립(linearly independent) 관계에 있어야 한다'는 것입니다. * 선형 독립 (Linearly Independent): 어떤 방정식도 다른 방정식들의 조합(상수배를 더하거나 빼는 등)으로 만들어질 수 없는 상태입니다. 기하학적으로 이는 3개의 평면(각 방정식은 3D 공간의 평면을 나타냄)이 단 한 개의 점(해)에서 만나는 것을 의미합니다. * 선형 종속 (Linearly Dependent): 하나 이상의 방정식이 다른 방정식들의 조합으로 표현될 수 있는 상태입니다. 이 경우, 새로운 정보를 제공하지 못하는 '잉여' 방정식이 존재하는 것입니다. 기하학적으로 이는 3개의 평면이 하나의 선에서 만나거나(무수히 많은 해), 완전히 겹치거나, 혹은 평행하여 만나지 않는(해가 없음) 상태를 의미합니다. 질문자님의 사례는 '선형 종속'이 되어 무수히 많은 해가 발생하는 경우입니다. 2025 12.30 질문하신 연립 방정식은 미지수가 3개이고 모두 1차인 3원 1차 연립방정식입니다. 이상적으로 문제가 없다면 {x,y,z} 에 대한 좌표가 하나 나오게 됩니다. 원하는 답 {52.5, -2.5, 15} 그런데 '두개 조건(식)을 그대로 두고 나머지 하나를 변형하다 보니, 원하는 답이 나오지 않는 상황이 발생하였다.'고 질문하신 상황입니다. 3개의 조건식이 주어진 3원 1차 연립방정식은 조건을 변형해서 하나의 변수를 제거할 수 있습니다. 그러면 2개의 조건식으로 주어지는 2원 1차 연립방정식으로 변형이 됩니다. ㄴ 꼭 변형해야하는 것은 아니지만, 이것이 알아보기 쉽기 때문에 변형시키는 것입니다. 변경하지 않은 2개 조건의 식(con1) 을 이용해 위와 같이 하나의 y & z 1차 방정식을 유도할 수 있는데요. 변경하는 나머지 1개의 방정식이 con1에서 유도된 방정식과 동일하다면 하나의 답이 구해지지 않는 상황이 발생하는 것입니다. 계산기(ti-nspire)는 {x,y,z} 의 답이 하나가 아니고 무수히 많음을 c1 을 이용해서 표현해 준 것입니다. linear_independence_cond12.tns 2025 12.30