계산기 사용시 (유효자릿수에 의한) 라운딩 처리 때문에 발생하는 오류 가능성, rounding errors
출처 : HP-15C ADVANCED FUNCTIONS HANDBOOK (p.145)
ㄴ Appendix : Accuracy of Numerical Calculations
Example 2: Many Pennies.
A corporation retains Susan as a scientific and engineering consultant at a fee of one penny per second for her thoughts, paid every second of every day for a year. Rather than distract her with the sounds of pennies dropping, the corporation proposes to deposit them for her into a bank account in which interest accrues at the rate of 11¼ percent per annum compounded every second. At year's end these pennies will accumulate to a sum
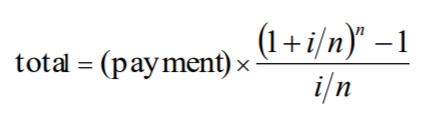
where
payment = $0.01 = one penny per second,
i = 0.1125 = 11.25 percent per annum interest rate,
n = 60×60×24×365 = number of seconds in a year.
Using her HP-15C, Susan reckons that the total will be $376,877.67. But at year's end the bank account is found to hold $333,783.35. Is Susan entitled to the $43,094.32 difference?
In both examples the discrepancies are caused by rounding errors that could have been avoided. This appendix explains how.
The war against error begins with a salvo against wishful thinking, which might confuse what we want with what we get. To avoid confusion, the true and calculated results must be given different names even though their difference may be so small that the distinction seems pedantic.
번역 ChatGPT-4o
출처: HP-15C 고급 기능 설명서 (p.145)
ㄴ 부록: 수치 계산의 정확도
예제 2: 많은 페니.
한 기업이 Susan을 과학 및 엔지니어링 컨설턴트로 고용하면서, 1년 365일 24시간의 매 초마다 그녀의 상상에 대해 1 페니를 지급하기로 한다. 기업은 Susan이 떨어지는 동전 소리에 방해받지 않도록 그녀에게 지급할 돈을 은행 계좌에 예치할 것이며, 그 계좌에는 11¼ 퍼센트의 연이율로 매초마다 복리 이자가 붙는다. 일 년 후 이 페니들은 다음과 같은 금액으로 불어날 것이다.
$$ total = (payment) × \frac {(1+\frac{i}{n})^{n}-1}{\frac{i}{n}} $$
여기서,
지급액 = $0.01 = 1 페니 / 1 sec,
i = 0.1125 = 연이율 11.25%,
n = 60×60×24×365 = 1년의 초 단위 수.
Susan은 그녀의 HP-15C를 사용해 총액이 $376,877.67 이 될 것으로 계산했다.
그러나 1년 후 계좌에 있는 금액은 $333,783.35 뿐이었다.
Susan은 $43,094.32 의 차액을 받을 자격이 있을까?
두 예제 모두 차이가 발생한 원인은 반올림 오류 때문이다. 이러한 오류는 피할 수 있었다. 이 부록에서는 그 이유를 설명한다.
오류와의 전쟁은 우리가 원하는 것과 얻는 것을 혼동할 수 있는 비현실적 기대를 겨냥한 포격으로 시작된다. 혼란을 피하기 위해, 진정한 결과와 계산된 결과에는 구별된 이름이 부여되어야 하며, 그 차이가 너무 작아 보잘것없어 보일지라도 구분해야 한다.
HP-15C는 1982년 출시해 1989년 단종된 공학용 계산기입니다. 구형 기종이다보니 계산에 사용된 유효자릿수가 크지 않았던 듯 싶습니다(찾아보니 10 자리네요).
이 예제에서는 그래서 발생한 오차율이 무려 12.91% 에 달하는데... 이 정도면 (이 용도로는) 못쓴다고 봐야 맞을 겁니다. (항상 검산하고 있을 수는 없잖아요)
그러니 설명서 appendix에 이와 관련하여 오차가 발생할 수 있음을 강력하게? 경고하고 있습니다. 경고할 수밖에 없겠죠. 이 데이터를 그대로 썻다가는... 끔찍한 사태가 발생할 수도 있으니까요. 물론 이 예제는 좀 극단적인 계산에 해당한다고 할 수 있겠습니다만...
Round-Off Error As mentioned earlier, the HP-15C holds every value to 10 digits internally. It also rounds the final result of every calculation to the 10th digit. Because the calculator can provide only a finite approximation for numbers such as π or 2/3 (0.666…), a small error due to rounding can occur. This error can be increased in lengthy calculations, but usually is insignificant. To accurately assess this effect for a given calculation requires numerical analysis beyond our scope and space here! Refer to the HP-15C Advanced Functions Handbook for a more detailed discussion.
60p. Section 5: The Display and Continuous Memory. HP-15C Owner’s Handbook. 20Edition 2.4, Sep 2011
참고 : https://en.wikipedia.org/wiki/HP-15C
문제가 발생한 원인
i/n = 0.1125 / (60 × 60 × 24 × 365) 까지는 문제가 없었지만...
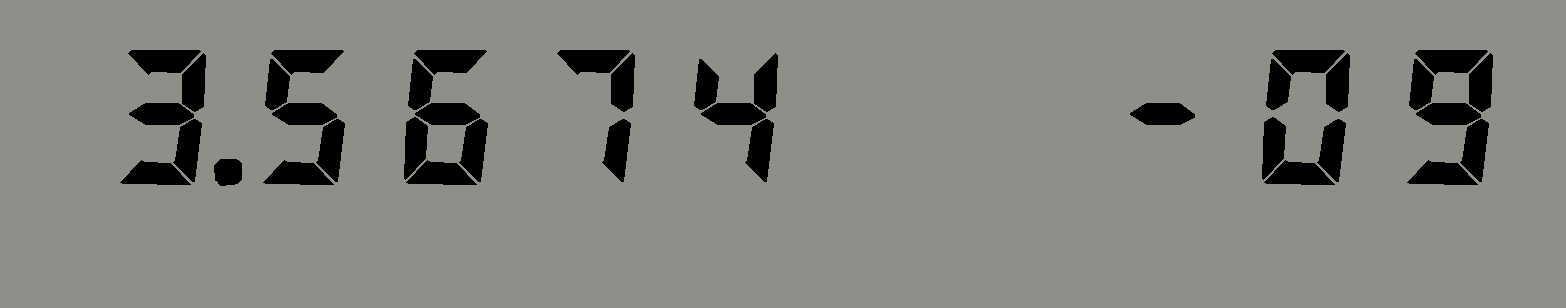
위의 값에 1을 더하는 순간 1 + i/n

화면 자릿수 표시 한계로 마지막 자릿수가 안보이니, 이 값에서 다시 1을 빼 보면

원래 이자율이 아니라 반올림된 "4" 가 남아 있습니다. 이자율이 달라진(올라간) 셈입니다.
요즘 계산기는 어떨까요? (feat. 울프람 알파)
https://www.wolframalpha.com/input?i=0.01*%28%28%281%2B%28%280.1125%29%2F%2860*60*24*365%29%29%29%5E%2860*60*24*365%29-1%29%2F%28%28%280.1125%29%2F%2860*60*24*365%29%29%29%29
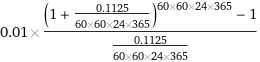
= 333783.34994842833172198487646142620143147263335390407812403560738...
≒ 333783.35
댓글10
-
세상의모든계산기
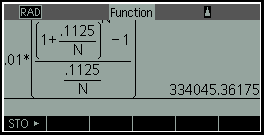
TI-nspire CX (CAS)
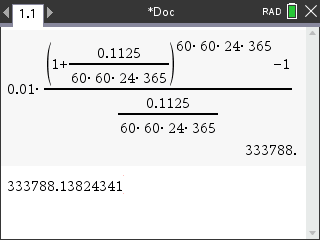
오차 ≒ 4.78829, 오차율 ≒ 0.0014%
-
세상의모든계산기
TI-nspire CX (CAS) Finance Solver
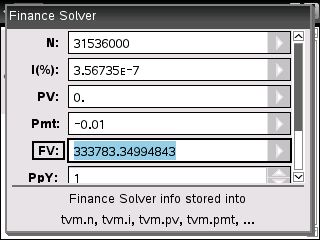
오차 ≒ 0.000000002 오차율 ≒ 0%
단지 우연인지??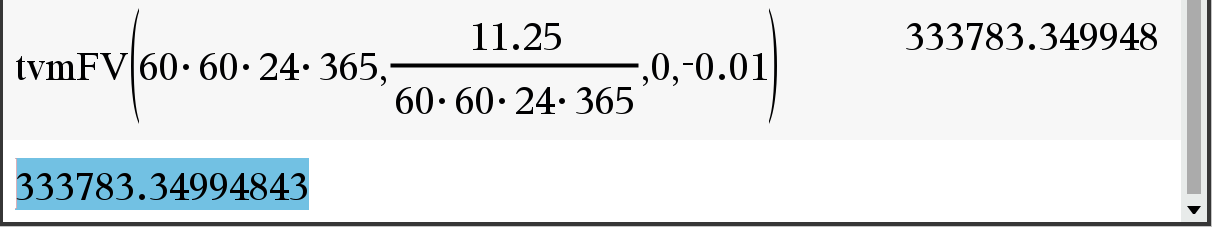
공식을 다른 (변형된) 걸 쓰나??
-
세상의모든계산기
HP 39gII
오차 ≒ 262.01175, 오차율 ≒ 0.0785%
-
세상의모든계산기
CASIO fx-570ES (Emul)
오차 ≒ -0.15815, 오차율 ≒ 0.0000474 %
* fx-991EX 결과 동일
-
세상의모든계산기
프로그램을 이용해서 순수하게 루프로만 계산
# 복리 계산 프로그램 # 매초 입금액: 0.01원 # 매초 이자율: 11.25%/(60*60*24*365) # 총 기간: 60*60*24*365 초 # 변수 초기화 deposit_per_second = 0.01 interest_rate_per_second = 11.25 / (60 * 60 * 24 * 365) / 100 total_seconds = 60 * 60 * 24 * 365 balance = 0 # 루프를 통한 복리 계산 for second in range(total_seconds): balance += deposit_per_second # 매초 입금 balance *= (1 + interest_rate_per_second) # 이자 적용 # 최종 잔고 출력 print(f"1년 후 최종 잔고는: {balance:.16f}원")결과 : 1년 후 최종 잔고는: 333783.3508975196164101원
더 정밀한 변수를 사용하면? getcontext().prec = 50
from decimal import Decimal, getcontext # Decimal의 정밀도 설정 getcontext().prec = 50 # 필요한 정밀도에 맞게 설정 # 변수 초기화 (Decimal 사용) deposit_per_second = Decimal('0.01') interest_rate_per_second = Decimal('11.25') / (60 * 60 * 24 * 365 * 100) total_seconds = 60 * 60 * 24 * 365 balance = Decimal('0') # 루프를 통한 복리 계산 for second in range(total_seconds): balance += deposit_per_second # 매초 입금 balance *= (1 + interest_rate_per_second) # 이자 적용 # 최종 잔고 출력 print(f"1년 후 최종 잔고는: {balance:.100f}원")1년 후 최종 잔고는: 333783.3511391508986042206488714749901779988494135500000000000000000000000000000000000000000000000000000000원 // getcontext().prec = 50
1년 후 최종 잔고는: 333783.3511391508986042206488714749901779987514741688945977231006921793358689473965341940033140160948000000원 // getcontext().prec = 100
-
세상의모든계산기
문득 루프로 돌리는게 정확할까? 공식에 넣어 계산하는게 정확할까? 궁금해 졌습니다.
처음에는 별 생각 없었는데(오차가 더 적을 거라는 기대가 있었던 것 같음)
생각해 보니 루프는 오차가 계속 누적되므로 루프 횟수가 많아질수록 오차가 커질 것 같음.from decimal import Decimal, getcontext # Decimal의 정밀도 설정 (100자리까지 계산) getcontext().prec = 100 # 변수 초기화 (Decimal 사용) deposit_per_second = Decimal('0.01') interest_rate_per_second = Decimal('11.25') / (60 * 60 * 24 * 365 * 100) total_seconds = 60 * 60 * 24 * 365 balance_loop = Decimal('0') # 루프를 통한 복리 계산 for second in range(total_seconds): balance_loop += deposit_per_second # 매초 입금 balance_loop *= (1 + interest_rate_per_second) # 이자 적용 # 공식에 맞는 정확한 계산 (fvaf) annual_interest_rate = Decimal('11.25') / 100 # 11.25% 연이자율 n = total_seconds # 총 복리 계산 횟수 (초 단위로 계산) fvaf = ((1 + annual_interest_rate / n) ** n - 1) / (annual_interest_rate / n) # 연금의 내가계수 공식 balance_fvaf = deposit_per_second * fvaf # 공식에 따른 미래 가치 # 결과 출력 print(f"루프를 통한 계산 결과: {balance_loop:.100f}원") print(f"공식에 따른 계산 결과: {balance_fvaf:.100f}원")루프를 통한 계산 결과: 333783.3511391508986042206488714749901779987514741688945977231006921793358689473965341940033140160948000000원
공식에 따른 계산 결과: 333783.3499484283317219848764614262014314726333539040781240356073844039099828033112644904100722067345000000원* 울프람 알파는 일단 결과로 보여지는 자릿수까지는 모두 공식에 의해 정확한 값을 보여주고, 【More Digits】 버튼을 누르면 그에 따라 정밀도를 높여 다시 계산하는 것 같습니다.




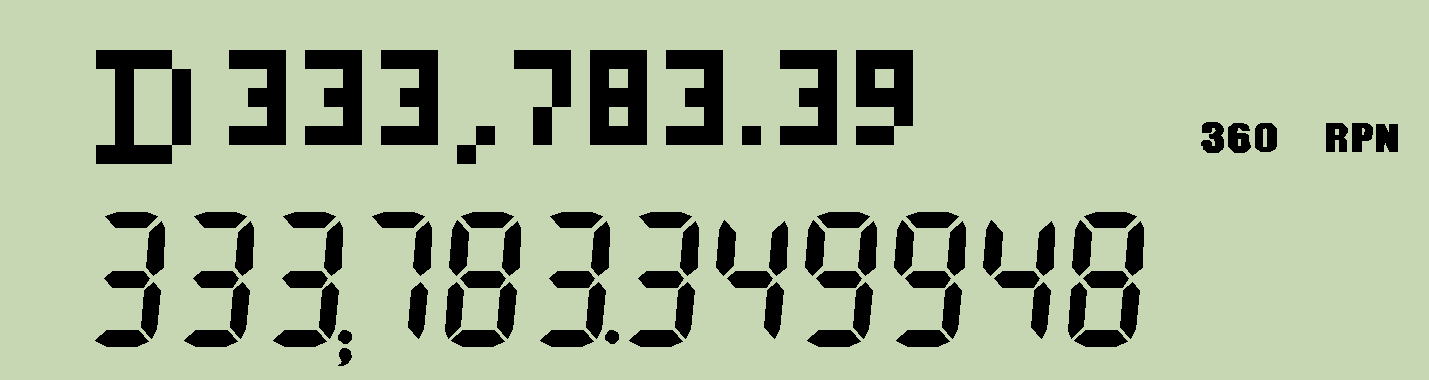
세상의모든계산기 님의 최근 댓글
기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04