[일반 계산기] 세제곱근 구하기. 방법#1, 정수제곱근법 & 뉴튼-랩슨법을 이용한 반복계산
-
- 2024.10.14 - 10:07 2015.01.18 - 00:43 31060 15
세제곱근 버튼이 없는 일반 계산기로 세제곱근을 구할 수 있을까요?
$$ \sqrt[3]{a} = ? $$
구할 방법이 없는 것은 아니지만, 누군가 물어본다면 "일반 계산기로는 세제곱근을 구할 수 없다"고 말하는게 좋겠습니다.
왜냐하면 직접 그 값을 구하는 것도 쉽지 않을 뿐 아니라, 상대방을 이해시키는 것도 쉽지 않기 때문입니다.
그래도 그 방법을 알고 싶으시다면... 계속 읽어보세요.
따라하실 분은 자릿수가 최대한 많은 계산기로 따라하시구요.
반올림 설정하시고, 자릿수는 F로 설정하세요.
방법1 : 계산기 정수 제곱근법을 이용
1. 처음 1회만 입력할 버튼순서 : 【a】【√】【√】
2. 계속 반복하여 입력할 버튼 순서 : 【×】【a】【=】【√】【√】
- 반복입력하는 버튼의 순서는 계산기의 상수계산 방식에 따라 다를 수 있습니다. (Casio vs Sharp)
- 이 방법에는 계산기의 루트 기능이 반드시 필요합니다.
- 12자리 계산기로 대략 19회 ~ 20회 정도 반복하면 최종 결과가 얻어집니다. (정답을 찾을 때)
총 버튼 입력 횟수 = 3+(5×20) = 103회
※ 단순히 근사값으로 충분한 경우에는 5회~6회 반복으로 만족하는게 좋습니다. - 위의 방식을 확장하면, 7제곱근(7=2^3-1)이나, 15제곱근(=2^4-1) 등을 구할 수도 있습니다.
제곱이 반복될수록 반복해 입력할 버튼횟수는 반대로 줄어듭니다.
예제 동영상) 0.1의 세제곱근
위 계산 결과는 아래와 같이 정답에 수렴해 갑니다.
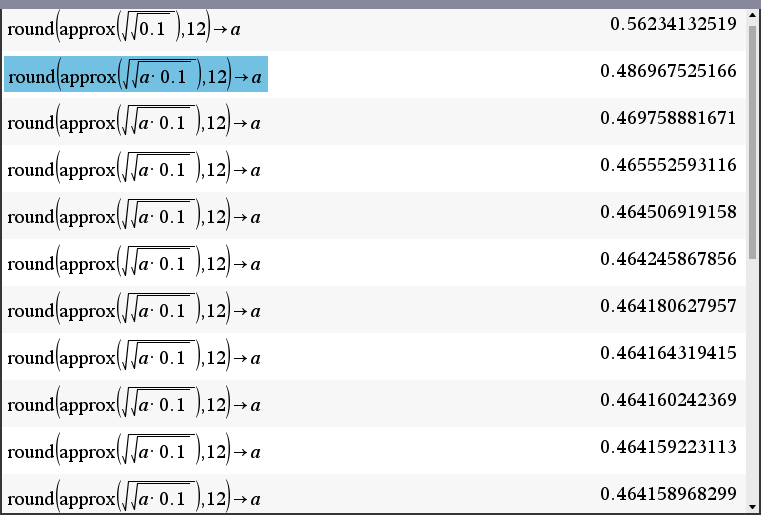
$ \sqrt[3]{0.1} = 0.4641588833612... $
방법2 : 뉴튼 랩슨법 Newton-Raphson Method 을 이용
1. 초기값 (대략 추정하여) 입력 
【CM】【M+】
2. 이후에 반복 : 【=】【=】【×】【2】【+】【a】【÷】【3】【÷】【RM】【=】【=】【CM】【M+】
└ 위 반복입력식은 (일반)계산기의 "상수계산" 방식에 따라 달라질 수 있습니다. (Casio vs Sharp)
- 이 방법은 루트 버튼은 필요 없지만, 메모리 M 기능이 필요합니다.
- 반복 순서를 외우는게 좀 복잡하지만
방법1보다는 입력횟수가 조금 적습니다.
대략 5~6회 정도 반복하면 최종 결과가 얻어집니다.
(6회 반복시 총 버튼 입력 횟수 = 1 + 15*6 = 91회)
이게 정말 될까? 
예제 동영상) 7의 세제곱근을 구하는 동영상입니다.
근데... 이걸 왜 하고 있는거죠??
n제곱근을 구하는 다른 접근 방법 - 로그 성질의 활용
https://allcalc.org/49753
-
25
댓글15
-
-
1
세상의모든계산기
그 외 n제곱근의 계산
이 원리를 확대 적용하면
일반 계산기를 이용해서 (8-1)=7 제곱근 (16-1)=15제곱근... 등등을 비교적 쉽게 구할 수 있습니다.
3, 7, 15, 31, 63, 127, ... (2^n-1)
그리고, 그 값을 활용해 그 외 제곱근도 (일부?) 구할 수 있죠.
제곱근 : 【√】
3제곱근 : 본문 방법으로 구함. (4제곱근의 활용.【√】【√】)
4제곱근 : 【√】【√】
5제곱근 : 15제곱근(【√】【√】【√】【√】)의 3승. // 5 = 15 ÷ 3 (즉, 1/5 = 3 ÷ 15)
6제곱근 : 제곱근 ÷ 3제곱근
7제곱근 : 본문 방법에서 【√】한번 더 추가.
8제곱근 : 【√】【√】【√】
9제곱근 : 3제곱근의 ▶ 3제곱근 으로 구할 수는 있는데... 두번째 세제곱근 구할 때 오차가 커질 수 있음.
10제곱근 : 15제곱근의 ▶ 제곱근의 ▶ 3승
11제곱근 : 1023제곱근(【√】【√】【√】【√】【√】【√】【√】【√】【√】【√】)의 ▶ 93승
ㄴ 오히려 쉬울 수도?12제곱근 : 3제곱근 ÷ 4제곱근 또는 6제곱근의 ▶ 제곱근
13제곱근 : 4095제곱근 ▶ 315승
ㄴ 그냥 근사값만 구한다면 64제곱근 ▶ 5승 으로 구할 수는 있음.
-
2
세상의모든계산기
2^8=256 이니까
255제곱근을 구할 수가 있구요
255 = 3 * 5 * 17
같은 방식으로
2^10 - 1 = 11 * 93
2^12 - 1 = 13 * 315
2^18 - 1 = 19 * 13797
2^22 - 1 = 23 * 182361
2^28 - 1 = 29 * 925639532 제곱근까지는 모두 일단 이론적으로는 구할 수가 있는 걸로 나오는데...
아무리 일반 계산기에 상수계산(반복계산) 기능이 있어서 수백번까지야 무리해서 한다고 하더라도
그 이상 반복횟수가 많아지면 계산기의 마지막 자릿수 탈락에 의한 오차가 커지고,입력 횟수를 까먹는 등의 문제가 있어서 실질적으로 참값을 구하는건 불가능하겠습니다.
- 3
- 4
-
3
세상의모든계산기위 방식으로 7의 17제곱근을 구해 봤습니다.
255제곱근
17제곱근
공학용 계산기(비교)
1.0076602106307
1.1212737354259
쌀집 계산기
1.00766021062
1.12127373515
255제곱근 구하는 것도 생각보다 빠르고 (반복4회, 53버튼입력)그 값의 15승 구하는 것도 생각보다 빠릅니다. (15버튼입력)(총 68 버튼입력)오차도 생각보다 크지 않구요. 이정도면 만족스럽습니다.하지만 그 이상은 버튼 입력 횟수가 급격히 늘어나서직접 사용하기가 어려울 듯 하네요. -
세상의모든계산기
뉴튼 랩슨법 : 일반해를 구하는 방법
http://en.wikipedia.org/wiki/Newton%27s_method
따라서 모든 n제곱근 값을 구할 수 있습니다. (초기값 설정에 따른 오차가능성은 있습니다만...)
* 여기서 Xk는 k번째 결과, X(k+1)은 k+1번째 결과입니다.
제곱근
(초기값)
1
a
2
3제곱근
==
2
3
==
4제곱근
===
3
4
===
n제곱근
=
(n-1)번
n-1
n
=
(n-1)번
※ 카시오 계산기의 경우 상수 계산 방식이 달라서 입력 횟수와 방식이 약간 다릅니다.
- 1
-
세상의모든계산기
예시 : 1.7055^(1/7) - 1 = ?
ㄴ (링크) 지식인 질문 & 답변
ㄴ 지수가 1/7로 단순하니 로그 성질을 활용한 방법도 가능합니다. : https://allcalc.org/49753
-
세상의모든계산기
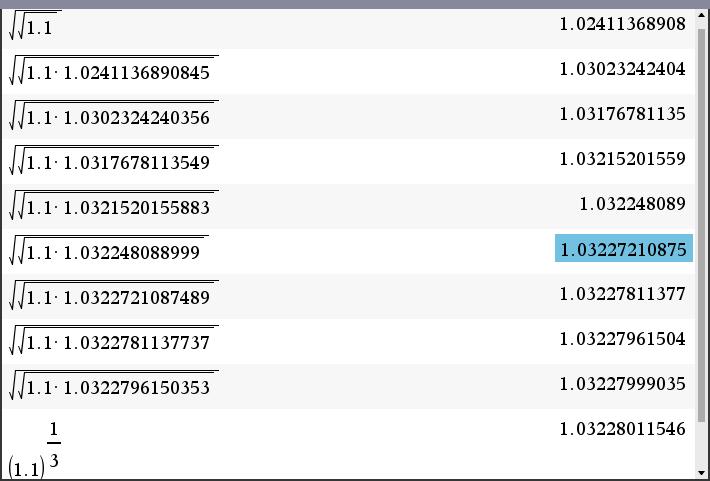
예시 : 수익률 기하평균
1.1^(1/3) -1 = ?
-
세상의모든계산기
뉴턴-랩슨 방법을 이용한 제곱근 계산
뉴턴-랩슨 방법은 근을 구하는 반복적인 알고리즘입니다. 루트 값을 구하는데 매우 효과적입니다. 예를 들어,
를 구하려고 할 때 다음과 같은 단계를 따릅니다.
1. 초기 추정값 을 선택합니다. 보통 의 절반 값이 괜찮은 초기값입니다.
2. 다음 반복식을 사용하여 새로운 추정값을 계산합니다:
3. 원하는 정확도에 도달할 때까지 2단계를 반복합니다.
예시를 들어보겠습니다. 를 구하는 과정을 설명하겠습니다.
1. 초기값 을 5로 설정합니다 (10의 절반).
2. 첫 번째 반복:
3. 두 번째 반복:
4. 세 번째 반복:
5. 네 번째 반복:
이 과정을 반복하면 원하는 정확도에 도달할 때까지 계속 계산할 수 있습니다. 일반적으로 4~5번 정도 반복하면 소수점 이하 몇 자리까지 정확한 값을 얻을 수 있습니다.
이 방법을 사용하면 일반 계산기에서도 루트 값을 구할 수 있습니다. 몇 번의 반복을 통해 상당히 정확한 값을 얻을 수 있습니다.
-
세상의모든계산기
예시 : 5제곱근 구하기. $ \sqrt[5]{123} $
계산 순서 ⓐ 15제곱근을 구하고, ⓑ 그 값을 3제곱
ⓐ 15제곱근 값 구하기 (3회 반복, 루트 기능 이용)
키 입력 : 【123】【√】【√】【√】【√】
(√123 = 11.090536506409)
(√11.090536506409 = 3.3302457126178)
(√3.3302457126178 = 1.8248960826901)
(√1.8248960826901 = 1.3508871465412)키 입력 : 【×】【123】【=】【√】【√】【√】【√】
1.3508871465412 × 123 = 166.15911902457
(√166.15911902457 = 12.890272263400)
(√12.890272263400 = 3.5903025309018)
(√3.5903025309018 = 1.8948093653193)
(√1.8948093653193 = 1.3765207464180)키 입력 : 【×】【123】【=】【√】【√】【√】【√】
1.3765207464180 × 123 = 169.31205180941
(√169.31205180941 = 13.011996457478)
(√13.011996457478 = 3.6072145011737)
(√3.6072145011737 = 1.8992668325366)
(√1.8992668325366 = 1.3781389017572)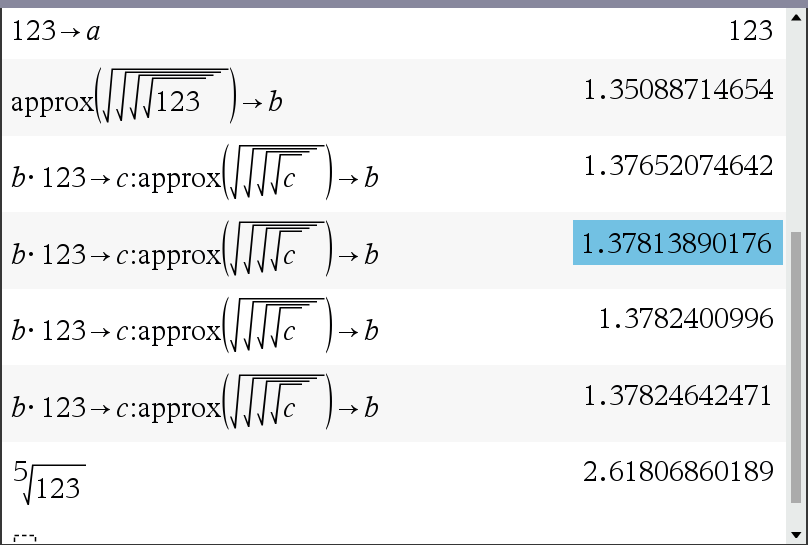
ㄴ 3회 반복하여 파란색 결과에서 멈추었습니다.
ㄴ 횟수가 반복될수록 더 정확한 값에 수렴합니다만, 득실관계(trade-off)를 따져야 합니다. 시간투자 + 버튼 입력 실수 가능성.
ⓑ 3제곱 값 구하기 (상수계산 기능 이용)
(Non-K 타입) 키 입력 : 【×】【=】【=】
1.3781389017572 × = 1.8992668325365 // ⓐ의 제곱 값
× 1.3781389017572 = 2.6174535067357 // ⓐ의 세제곱 값ⓒ 참값과 ⓑ의 결과 값 비교 (오차율 확인, 꼭 확인할 필요는 없음)
0.02% 오차면 잘 구해졌죠.
주의 : 키 입력 순서나 방법 그리고, 결과값의 오차수준은 계산기 모델에 따라 다를 수 있습니다.
- 실물 계산기로 적용한 결과
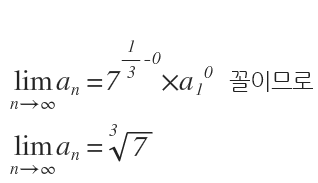
세상의모든계산기 님의 최근 댓글
- claude AI는 l-c*r^2 을 1-c*r^2 으로 잘못 읽고 표시하고 있습니다. - TI-nspire CAS 계산기에 l-c*r^2 ≥0 을 조건에 추가해 계산해 보아도 결과는 바뀌지 않습니다. 2026 07.20 ⚠️ 경고가 바로 두 번째 방법이 "성공"한 이유와 정확히 연결되어 있습니다. 경고의 의미 "Domain of the result might be larger than the domain of the input"는 CAS가 절댓값(모듈러스)을 계산하는 과정에서 원래 식보다 정의역이 더 넓은 형태로 단순화했다는 뜻입니다. 구체적으로 이 계산은 내부적으로 대략 이런 과정을 거칩니다. $$\left|\frac{er}{e\cdot r}\right| = \sqrt{\left(\frac{er}{e\cdot r}\right)\cdot\overline{\left(\frac{er}{e\cdot r}\right)}}$$ 즉 원래 식(복소수)과 그 켤레복소수를 곱해서 실수부·허수부 제곱합을 만들고, 거기에 다시 제곱근을 씌우는 과정입니다. 이 과정에서 √(x²) → x 또는 √a·√b → √(ab) 같은 규칙들이 쓰이는데, 이런 규칙들은 x가 실수이고 0 이상일 때만 엄밀하게 성립합니다. CAS는 이 조건들을 일일이 다 추적하지 않고 넘어가면서, 원래는 (e≠0, r+l·ω·i ≠ 0 등) 복소수 특유의 좁은 정의역을 가진 식을, r, l, ω가 어떤 실수여도(부호 무관하게) 정의되는 1/√(r²+l²·ω²)라는 더 넓은 정의역의 식으로 바꿔버린 것입니다. CAS는 이 손실을 감지하고 경고를 띄운 것입니다. 이게 왜 조건 대입 성공과 연결되는가 정리하면, 이 경고는 사실상 이런 뜻입니다. "나는 이 결과를 만들면서 원래 식이 가지고 있던 정의역 제약 정보(부호 조건, i 관련 조건 등)를 이미 버렸다." 바로 이 "정의역 정보를 버린" 상태가 이후 con_1 대입을 매끄럽게 만드는 원인입니다. 첫 번째 시도에서는 i가 살아있는 원래 식에 조건을 대입했기 때문에, CAS가 √(1-c·r²)이 실수인지(정의역 조건: 1-c·r² ≥ 0) 계속 추적하려고 했고, 그 정보가 con에 없어서 더 이상 정리를 못 하고 멈췄습니다. 두 번째 시도에서는 절댓값 계산 단계에서 이미 그런 세밀한 정의역 추적을 CAS 스스로 포기(단순화)했기 때문에, 이후 ω에 무리식을 대입해도 "이게 실수가 맞나?" 하는 검증 절차 없이 그냥 대수적으로 치환·정리해 버립니다. 그래서 깔끔하게 √c/√l이 나온 겁니다. 한 줄 요약 절댓값 계산 시 뜬 "정의역이 넓어졌을 수 있다"는 경고는, CAS가 그 순간에 원래 식의 엄밀한 조건(정의역)을 놓쳤다는 신호이고, 바로 그 "조건을 놓친 상태"이기 때문에 뒤에 이어지는 조건식 대입이 막힘없이 진행된 것입니다. 다만 그 대가로, 결과인 1/√(r²+l²·ω²)이나 최종 √c/√l이 원래 회로 조건(i≠0이 되는 경계, 분모가 0이 되는 경우 등)에서는 엄밀히 성립하지 않을 수 있다는 점은 감안하셔야 합니다. 실제 물리적으로는 r, l, c > 0이고 결과도 물리적으로 타당한 형태라 문제없어 보이지만, 수학적 엄밀성 측면에서는 "정의역이 넓어진 근사적 결과"라는 꼬리표가 붙어있는 셈입니다. 2026 07.20 Claude AI 답변 TI-Nspire CAS의 | (such that / 조건대입) 연산자는 대입 시점의 수식 형태를 그대로 두고 기호만 치환하는 연산입니다. 대입 후에 처음부터 다시 "실수부/허수부 분리, 유리화" 같은 재간소화를 자동으로 수행하지 않습니다. 이 차이가 지금 보신 결과 차이의 핵심입니다. 첫 번째 경우 (|er/(e·r)| | con_1 and con → 실패) 이 시점의 식은 아직 r + l·ω·i 형태의 복소수 그대로입니다 (i가 살아있음). 여기에 con_1: ω = √(1-c·r²)/(√c·l)을 대입하면, 분모 안에 i · √(1-c·r²) 라는 항이 새로 생깁니다. 문제는 CAS가 √(1-c·r²)이 실수인지(즉 1-c·r² ≥ 0인지) 판단할 근거가 없다는 겁니다. 저장해 두신 con 조건은 c>0, l>0, r>0뿐이고, 1-c·r²≥0이라는 조건은 포함되어 있지 않습니다. 그래서 CAS는 i와 이 무리식을 더 정리(유리화, 실수부·허수부 재결합)하지 못하고 있는 그대로 남겨둡니다. 결과에 여전히 i가 보이는 이유입니다. 두 번째 경우 (결과값 1/√(r²+l²·ω²)에 대입 → 성공) |er/(e·r)| (절댓값/모듈러스) 연산은 그 자체로 이미 "복소수 → 실수" 변환을 완료한 결과입니다. 즉 1/√(r²+l²·ω²)에는 더 이상 i가 없고, 순수하게 r, l, ω로만 이루어진 실수식입니다. 이 식에 ω = con_1을 대입하는 것은 그냥 실수 대수식에 실수 대입하는 것이므로, i와 무리식이 뒤엉키는 문제 자체가 발생하지 않습니다. 그래서 바로 깔끔하게 √c/√l로 정리됩니다. 정리하면 절댓값(모듈러스) 계산은 "이 값들이 실수다"라는 가정을 이미 내부적으로 써서 i를 제거하는 연산입니다. 그 연산을 조건 대입 이전에 해두면, 이후 대입은 단순 실수 대입이라 문제없이 정리됩니다. 반대로 i가 남아있는 식에 무리식을 포함한 조건을 먼저 대입하면, 그 무리식의 실수성/부호에 대한 가정이 없어서 CAS가 i를 소거하는 재간소화를 못 하고 멈춰버립니다. 실용적 팁: 복소식에 조건을 대입해야 할 때는 가능하면 절댓값·실수화(유리화) 등을 먼저 끝내서 i를 없앤 뒤 조건을 대입하거나, 대입 후 결과에 다시 simplify/expand/combine 같은 명령을 한 번 더 걸어주면 (필요한 도메인 조건과 함께) 정리가 되는 경우가 많습니다. 2026 07.19 저도 어림잡아 추측할 뿐이지 정확한 이유를 알지는 못합니다. 질문하신 사진을 그대로 (Gemini 3.5 Flash / ChatGPT / Claude Sonnet 5) AI에 넣어 보니 claude AI 가 제일 합리적인 답변을 주어서 이를 붙여 넣습니다. 2026 07.19 아 그렇네요. 감사합니다. ^^ 2026 04.28