- 세상의 모든 계산기 자유(질문) 게시판 일반 ()
AlphaGo Zero: Learning from scratch (A.K.A 제파고)
-
- 2021.08.23 - 22:42 2017.10.19 - 09:00 1501 7
드디어 알파고의 마지막 행보 중 하나인 알파고 논문이 발표 되었습니다.
https://deepmind.com/blog/alphago-zero-learning-scratch/
아직 자세하게 읽어보진 않았지만 알파고 개발사에 대한 총정리 버전이 될 것 같습니다.
네이쳐 논문 링크 : https://www.nature.com/articles/nature24270.epdf?author_access_token=VJXbVjaSHxFoctQQ4p2k4tRgN0jAjWel9jnR3ZoTv0PVW4gB86EEpGqTRDtpIz-2rmo8-KG06gqVobU5NSCFeHILHcVFUeMsbvwS-lxjqQGg98faovwjxeTUgZAUMnRQ
눈에 띄는 점
1. Alpago Zero (A.K.A 제파고) 가 등장했습니다.
인간 기보 학습이나 인간의 어떠한 수동 조작(개입) 없이 오직 self-play training 로만 성장하게 만든 것이 Alphago Zero(A.K.A 제파고)입니다. 이러한 방법으로 단 3일만에 이전 논문의 알파고(=돌파고) 를 압살하는 수준까지 성장할 수 있었으며, 커파고(=마파고=Master) 수준까지는 21일, 커파고 보다 훨 쎈 수준까지는 40일(총 2900만판의 self-play)이 걸렸다고 말하고 있습니다. (40 Block 기준)
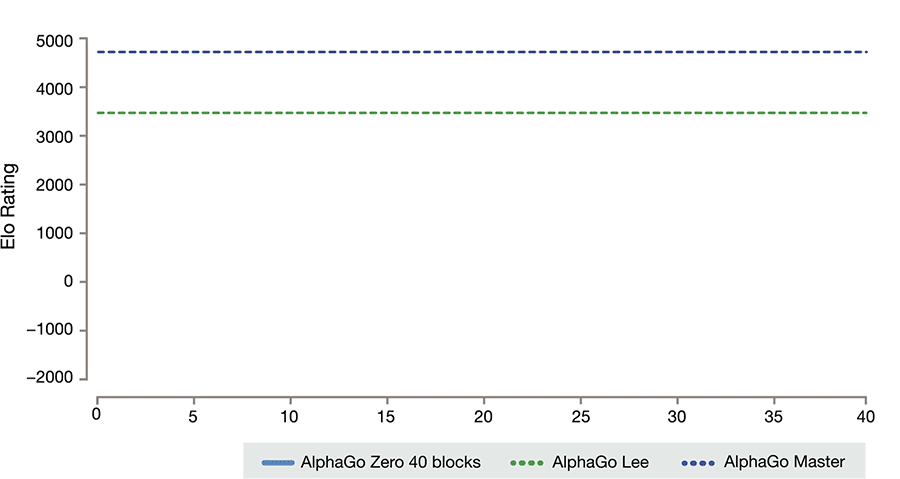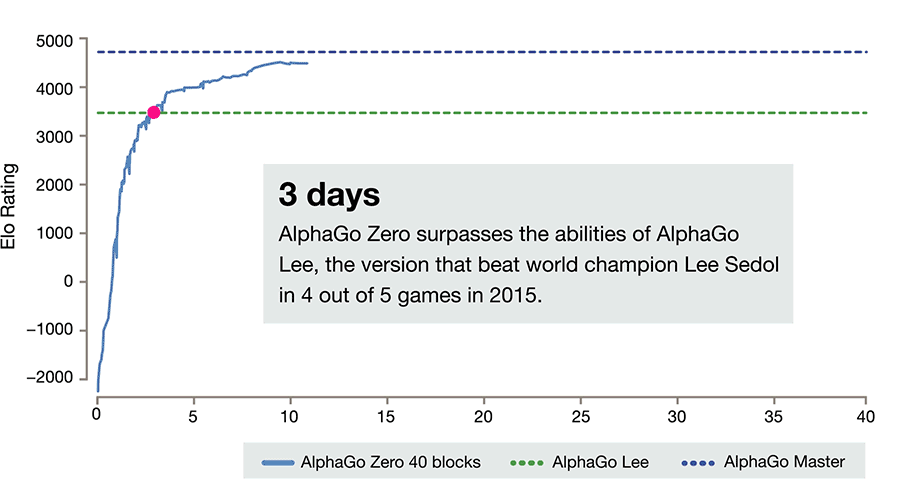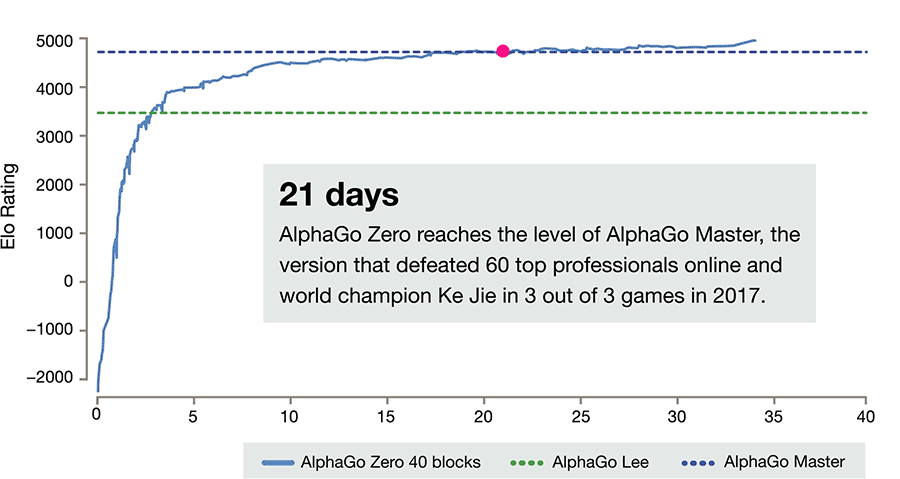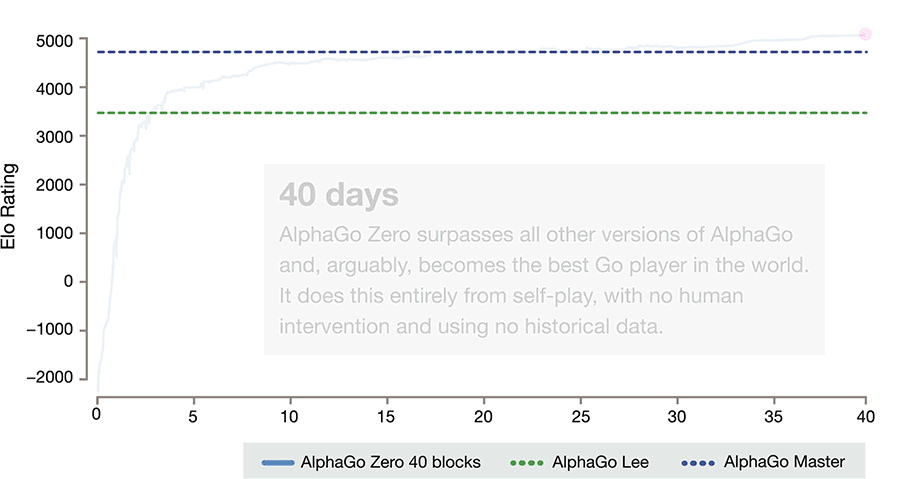
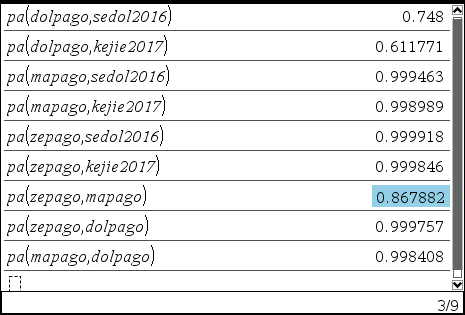
* 논문에 따르면 제파고(완성 버전)가 마파고를 89승 11패로 이겼다고 합니다. (게임당 2시간짜리 시합)
2. 기존 알파고와의 차이
기존 알파고들은 가치망(=승률분석), 정책망(=가능성 있는 다음 수 예측)이라는 2가지 신경망을 사용하였는데, 제파고는 이 둘을 통합한 단일 신경망으로 승률분석과 다음 수 예측을 모두 수행한다고 합니다. 그것이 학습이나 가치판단에 더 효율적이었다는 설명입니다.
그리고 제파고는 "rollouts" 를 하지 않는다고 합니다. (이건 잘 모르겠습니다)
* rollout = fast, random games used by other Go programs to predict which player will win from the current board position
틀린 예측 (알파고에 대한 오해)
- TPU 를 보고 놀란 나머지 이전 논문에 적힌 GPU 도 혹시 TPU 인 것은 아닐까 의심했습니다.
http://www.allcalc.org/18193
"TPU 를 썼지만 공개할 시점이 아니라서 GPU 숫자로 적당히 에둘러서 표현한 것은 아닐까?" 이런 의심이었는데...
틀렸네요. 초기버전(판파고)은 GPU로 개발했고, 중간에(돌파고부터) TPU(ver.1) 로 갈아탄게 확인되었습니다.
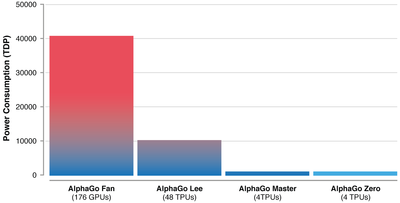
- 돌파고(=Alphago V.18) ELO Rating 이 4500 이라는 스샷이 올라온 적이 있습니다.
http://www.allcalc.org/16539
그런데 이번 발표(그래프)를 통해서 보면 돌파고의 Elo Rating 은 3700~3800 정도로 표시되었습니다.
당시에도 같거나 더 높은 수준의 (다양한) 상대방이 없어서 (이기는 게임만 하다보니) 레이팅에 인플레이션이 있는 것 같다는 말이 있었습니다만, 제파고(의 성장)를 기준으로 Elo Rating 이 재정립된 것 같습니다.
오늘(17.10.19) 기준으로 cgos 에 있는 탑 클래스의 딥젠고 ELO가 4000 내외 수준인데 이것도 더 높은 수준의 상대내지 동급의 상대와 두는 바둑의 횟수가 늘어나면 비슷한 과정을 겪을 것 같고, 인간 최고 수준(커박)의 ELO도 인공지능과의 대국을 추가하여 재평가한다면 다소나마 약간씩 떨어질 가능성이 있어 보입니다.
* [수정] 논문에 보면 Alphago Fan(3144), Lee(3739), Master(4858), Zero(5185) 로 정확하게 나와 있습니다. 그리고, 그 산출 근거를 다음과 같이 적시하였습니다. "The results of the matches of AlphaGo Fan against Fan Hui and AlphaGo Lee against Lee Sedol were also included to ground the scale to human references, as otherwise the Elo ratings of AlphaGo are unrealistically high due to self-play bias." 알파고끼리의(아마도 여타 AI 포함일 듯) 셀프대국만 반영하면 편향으로 인해 레이팅값이 비현실적으로 높아지는데, 이를 막기 위해 인간(판후이& 이세돌)과의 대결 결과를 인간 기준 척도의 기준점으로 삼았다고 밝혔습니다. 만약 돌파고 레이팅 4500이 인간대상으로도 통하였다면 3550인 이세돌과 대국에서 승리할 확률이 99.58% 라는 말인데, 4승1패를 설명하기가 너무 곤혹스러웠던 것 같습니다.
그럼에도 불구하고 4500을 3739로 깍은 것은 너무 과격?한 것이 아닌가 싶기도 합니다. '인간과의 대결 횟수가 너무 적기 때문'입니다. 그리고 왜 판파고의 레이팅(3144)은 왜 조정하지 않았을까요? 좀 더 자세히 알아볼 필요가 있을 것 같습니다.
- 돌파고(=Alphago V.18) ELO Rating 이 4500 이라는 스샷이 올라온 적이 있습니다.
결론
제목(Learning from scratch)에서 알 수 있듯, 이번 논문의 핵심은 "인간의 개입 없이, AI의 자력으로만 바둑이라는 Category를 마스터하였으며, 그것은 인류가 아직 도달하지 못한 미지의 영역이다."는데 있겠습니다.
딥마인드(구글)은 이러한 AI의 활동 분야를 바둑이라는 Category 에 한정하지 않고 넓혀 나갈 것이고, 그로 인해 인류가 아직 밟아보지 못한 수많은 길이 새로이 열릴 것입니다.
-
25
댓글7
-
세상의모든계산기
의문점1 : 제파고의 성장은 계속될 것인가? 아니면 어느 점으로 수렴할 것인가?
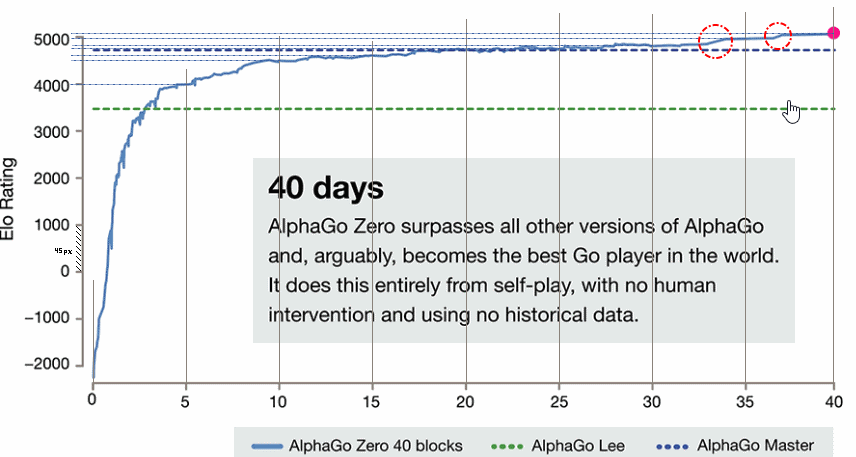
의문점2 : "완성 단계?에 이른 것인지, 성장이 더뎌졌다" 고 판단되어지는 33일 이후에 갑자기 도약하듯? 2차례 성장하였는데 제파고 내부에 어떤 변화가 있었던 것일까? (특정 정석에 대한 선택? 버림? 때문일까?)
-
세상의모든계산기
Rollout 과 관련하여 논문에 나온 내용을 뽑아보겠습니다.
- Finally, it uses a simpler tree search that relies upon this single neural network to evaluate positions and sample moves, without performing any Monte-Carlo rollouts.
- In each position st, a Monte-Carlo tree search (MCTS) αθ is executed (see Figure 2) using the latest neural network fθ. Moves are selected according to the search probabilities computed by the MCTS, at ~ πt.
- Figure 2: Monte-Carlo tree search in AlphaGo Zero.
- Monte-Carlo tree search (MCTS) may also be viewed as a form of self-play reinforcement learning.
- MCTS programs have previously achieved strong amateur level in Go, but used substantial domain expertise: a fast rollout policy, based on handcrafted features, that evaluates positions by running simulations until the end of the game; and a tree policy, also based on handcrafted features, that selects moves within the search tree.
this single neural network to evaluate positions and sample moves,without performing any Monte Carlo rollouts. -
세상의모든계산기
MCTS 를 여전히? 사용하여 (완전 랜덤은 아니지만) random 한 게임을 진행하는 것은 맞다.
마파고까지의 프로그램들은 승률 계산을 위해 rollouts(=빠르게 MCTS를 돌리는 것) 을 사용하였는데, 승률 계산을 다른 영역에 맏기므로 rollout을 할 필요가 없다.
이런 결론이네요.
Compared to the MCTS in AlphaGo Fan and AlphaGo Lee, the principal differences are that AlphaGo Zero does not use any rollouts; it uses a single neural network instead of separate policy and value networks; leaf nodes are always expanded, rather than using dynamic expansion; each search thread simply waits for the neural network evaluation, rather than performing evaluation and backup asynchronously; and there is no tree policy. A transposition table was also used in the large (40 block, 40 day) instance of AlphaGo Zero.
-
세상의모든계산기 님의 최근 댓글
V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04 1. 분모 먼저 계산 400 × 10000 = 100 × 6000 = GT 결과값 4,600,000 역수 처리 ÷÷== 결과값 0.00000021739 2. 분자 곱하기 ×3 00 00 00 ×4 00 ×1 00 00 최종 결과 = 2,608,695.65217 2026 02.04 해결 방법 1. t=-1 을 기준으로 그래프를 2개로 나누어 표현 ㄴ 근데 이것도 tstep을 맞추지 않으면 문제가 발생할 것기도 하고, 상관이 없을 것 같기도 하고... 모르겠네요. 2. t=-1 이 직접 계산되도록 tstep을 적절하게 조정 tstep=0.1 tstep=0.01 도 해 보고 싶지만, 구간 크기에 따라 최소 tstep 이 변하는지 여기서는 0.01로 설정해도 0.015로 바뀌어버립니다. 그래서 tstep=0.02 로 하는게 최대한 긴 그래프를 얻을 수 있습니다. 2026 02.02 불연속 그래프 ti-nspire는 수학자처럼 연속적인 선을 그리는 것이 아니라, 정해진 `tstep` 간격으로 점을 찍고 그 점들을 직선으로 연결하는 'connect-the-dots' 방식으로 그래프를 그립니다. 여기에 tstep 간격에 따라 특이점(분모=0)이 제외되어 문제가 나타난 것입니다. seq(−2+0.13*t,t,0,23) {−2.,−1.87,−1.74,−1.61,−1.48,−1.35,−1.22,−1.09,−0.96,−0.83,−0.7,−0.57,−0.44,−0.31,−0.18,−0.05,0.08,0.21,0.34,0.47,0.6,0.73,0.86,0.99} t=-1 에서 그래프를 찾지 않습니다. 그 좌우 값인 −1.09, −0.96 두 값의 그래프값을 찾고, Window 범위를 보고 적당히 (연속되도록) 이어서 그래프를 완성하는 방식입니다. 그래서 t=-1에서도 그래프 값이 존재하는 것입니다. 2026 02.02