테일러 급수 Taylor Series
테일러 급수(Taylor series)는 함수 \( f(x) \)를 주어진 점 \( a \)를 중심으로 다항식의 형태로 근사하는 방법입니다.
이는 특정 점 주변에서 함수의 값을 근사하기 위해 함수의 도함수 값을 활용하여 무한급수의 형태로 표현합니다.
테일러 급수의 정의
주어진 함수 \( f(x) \)가 \( a \)에서 \( n \)차 미분 가능할 때, \( f(x) \)의 \( a \)를 중심으로 한 테일러 급수는 다음과 같이 정의됩니다:
\[
f(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \frac{f'''(a)}{3!}(x - a)^3 + \cdots
\]
즉, 일반적인 형태는 다음과 같습니다:
\[
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n
\]
여기서:
- \( f^{(n)}(a) \)는 \( f(x) \)의 \( n \)차 미분을 \( a \)에서 평가한 값입니다.
- \( n! \)는 \( n \)의 팩토리얼로, \( n! = n \times (n-1) \times \cdots \times 2 \times 1 \)입니다.
- \( (x - a)^n \)는 \( x \)와 \( a \)의 차이를 \( n \)차까지 곱한 것입니다.
테일러 급수의 적용
테일러 급수는 다음과 같은 경우에 유용합니다:
1. 근사 계산: 복잡한 함수를 다항식으로 근사하여 계산을 간단히 할 수 있습니다.
2. 해석적 함수 연구: 함수의 성질을 분석하고 극한, 연속성, 미분 가능성을 연구하는 데 도움을 줍니다.
3. 수치해석: 수치적 방법에서 많은 알고리즘의 근본이 됩니다.
예시
함수 \( e^x \)의 테일러 급수는 \( a = 0 \)을 중심으로 하면 다음과 같이 됩니다:
\[
e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}
\]
또한, \( \sin(x) \)의 테일러 급수는 다음과 같습니다:
\[
\sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1}
\]
이러한 테일러 급수는 \( x \)가 0에 가까운 경우 \( e^x \)와 \( \sin(x) \)의 값에 매우 잘 근사합니다.
결론
테일러 급수는 함수 근사의 강력한 도구로, 미적분학, 물리학, 공학 등 다양한 분야에서 널리 사용됩니다. 이를 통해 복잡한 함수도 간단한 다항식으로 접근하여 다양한 문제를 해결할 수 있습니다.
참고

http://navercast.naver.com/contents.nhn?rid=22&contents_id=5561
https://ko.wikipedia.org/wiki/%ED%85%8C%EC%9D%BC%EB%9F%AC_%EA%B8%89%EC%88%98
댓글 6
-
-
-
f(x) = e^x 의 테일러 급수 근사값 그래프
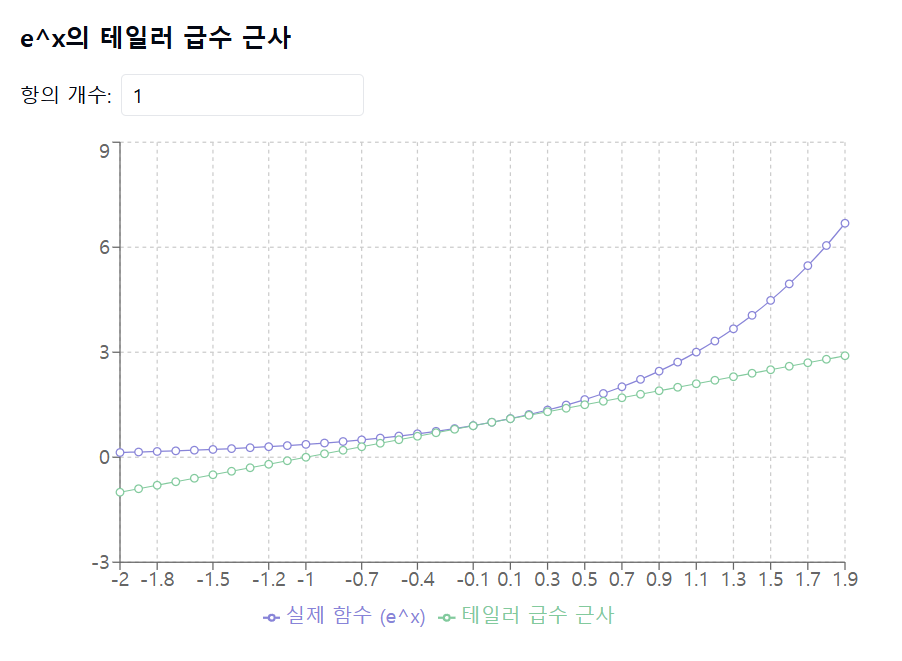
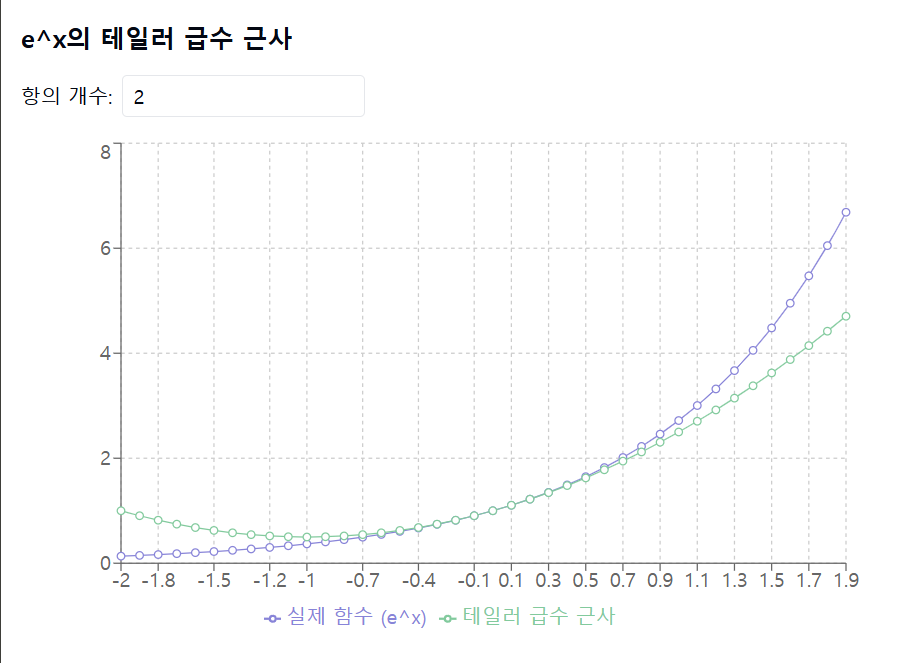
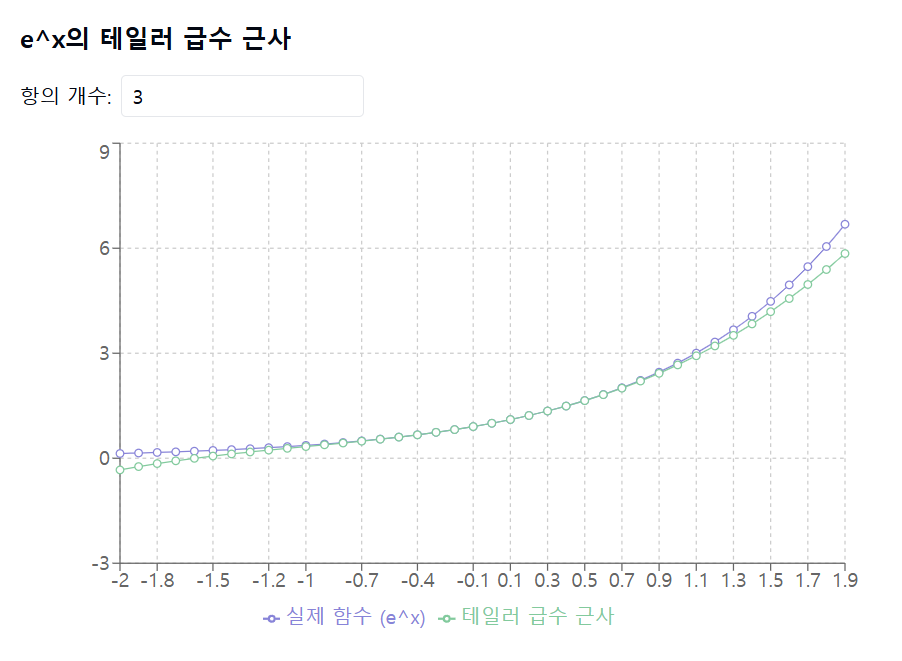
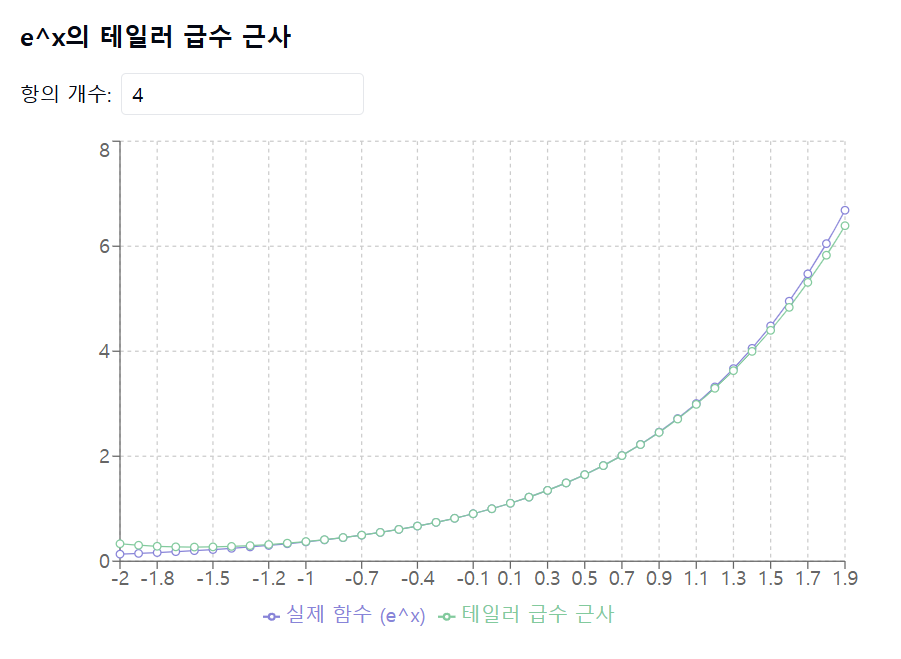
-
-
-
예시에서 0 을 중심으로 테일러 급수를 전개한 이유는?
테일러 급수를 0을 중심으로 전개하면 '매클로린 급수'라고도 불리는 특별한 경우의 테일러 급수가 됩니다.
- 계산의 단순화: 0을 중심으로 전개하면 계산이 상대적으로 간단해집니다. x^n 항의 계수가 f^(n)(0) / n!로 표현되어, 많은 함수에서 이 값을 쉽게 계산할 수 있습니다.
- 대칭성: 많은 중요한 함수들(예: e^x, sin(x), cos(x))이 원점에 대해 대칭적인 성질을 가집니다. 0을 중심으로 전개하면 이러한 대칭성을 잘 활용할 수 있습니다.
- 표준화: 0을 기준점으로 사용하면 다양한 함수들을 일관된 방식으로 비교하고 분석할 수 있습니다.
- 수학적 편의성: 많은 수학적 정리와 응용에서 0을 중심으로 한 급수 전개가 유용하게 사용됩니다.
- 오차 분석: 0 주변에서의 근사는 오차 분석이 상대적으로 쉽습니다.
-
-
-
$ 1.04^{\frac{2}{3}} $ 을 테일러 급수를 이용해 계산한다면?
테일러 급수 근사 계산기
-
-
-
테일러 급수의 오차 한계는?
테일러 급수에서 오차는 보통 테일러 급수의 n차 항까지 근사했을 때 실제 함수 값과의 차이로 정의됩니다.
이 오차를 나타내는 대표적인 표현이 테일러 정리의 나머지항(Remainder Term)입니다.
일반적으로 오차의 한계를 제시할 때는 라그랑주 잔여항(Lagrange Remainder) 또는 코시 잔여항(Cauchy Remainder)를 사용합니다.
만약 어떤 함수 \( f(x) \)를 \( a \)를 중심으로 한 테일러 급수로 근사한다고 할 때, 테일러 급수의 \( n \)차 항까지 근사한 오차는 다음과 같은 형태로 주어집니다.
라그랑주 잔여항에 의한 오차
라그랑주 잔여항 \( R_n(x) \)은 다음과 같이 표현됩니다:
\[
R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!} (x - a)^{n+1}
\]여기서:
- \( f^{(n+1)}(c) \)는 \( a \)와 \( x \) 사이의 어떤 점 \( c \)에서의 \( (n+1) \)차 미분값입니다.
- \( (n+1)! \)은 \( n+1 \) 팩토리얼입니다.
- \( (x - a)^{n+1} \)는 \( x \)와 중심 \( a \) 간의 거리의 \( (n+1) \)제곱입니다.- 테일러 전개를 통해 n번째 항까지 사용하였다면, n+1번째 항이 오차 한계에 해당함을 알 수 있습니다.
이 표현을 통해 오차의 크기를 다음과 같이 한정할 수 있습니다:
\[
|R_n(x)| \leq \frac{\max_{c \in [a, x]} |f^{(n+1)}(c)|}{(n+1)!} |x - a|^{n+1}
\]
따라서, 주어진 구간에서 \( f^{(n+1)}(c) \)의 최대값을 알면, 이 잔여항을 이용하여 테일러 급수 근사 오차의 한계를 추정할 수 있습니다.이 오차는 테일러 급수의 차수가 높아질수록 작아지며, 중심에 가까운 점일수록 더 정확한 근사를 제공합니다.
-
-
-
예) 구간[3,5] 에서 f(x)=√x 의 근사값을 a=4 에서의 2차 테일러 다항식을 이용하여 구할 때, 테일러 부등식에 의한 오차의 한계로 가장 적절한 것은?
(단, $ \dfrac{1}{3^{5/2}} \approx 0.064, \dfrac{1}{4^{5/2}} \approx 0.031, \dfrac{1}{5^{5/2}} \approx 0.018) $)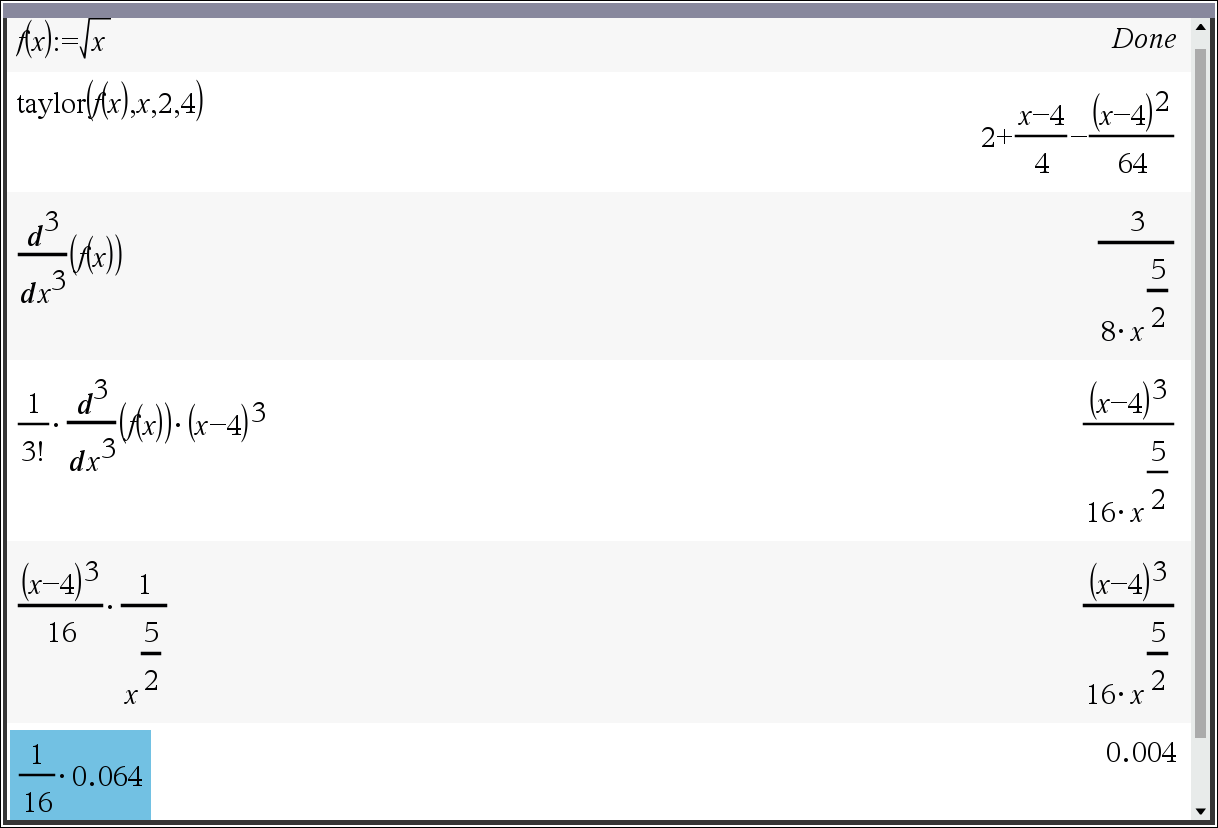
-


[TI-nspire] 의 taylor() 내장 함수
taylor(sin(x),x,13)
ㄴ 상단 : Degree, 하단 : Radian
* 이런 저런 이유로 각도 설정은 항상 Radian 으로 하는 것이 좋음.