떡밥 계산식 48÷2(9+3)=? 6÷2(1+2)=? 계산기에서의 결과는?
-
- 2025.10.28 - 15:11 2015.01.15 - 11:18 5423 25
한 때 인터넷을 떠들석 했던 바로 그 계산식!
지금도 가끔 사람들을 아리송하게 만드는 그 계산식!
48÷2(9+3) = ?
|
|
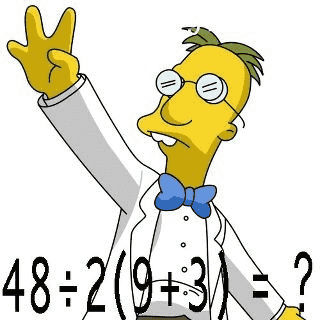
2파 |
288파 |
|
TI |
|
 └TI-89┘  └TI-30XIIS┘
|
|
CASIO |
 └fx-9860G┘
|
|
|
HP |
|
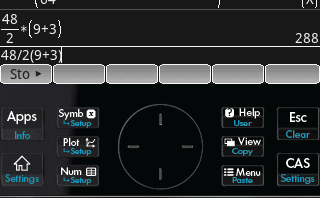 └HP Prime (HOME 모드)┘
|
|
SHARP |
 └EL-509W┘ |
|
|
기타 |
|
 └네이버 계산기┘
|
-
25
댓글25
-
세상의모든계산기
0. 두가지 물음
이 문제는 두가지 물음이 결합되어 있습니다.
첫번째 "주어진 수학식을
어떻게 해석할 것인가?" 라는 수학적인 물음두번째 "수학적으로는 잘못 표기된 수학식을 계산기에 그대로 입력했을 때
계산기는 어떻게 동작할 것인가?" 라는 공학적인 물음1. 수학적 물음 : 수식의 표기
본문의 수식은 "수학적으로 옳바르지 않은" = "정의되지 않은" 표기입니다.
그 이유는 수식에서 곱하기를 생략(Implied times sign)할 수 있는 경우는 "오해의 소지가 없는 경우"로 한정되기 때문입니다("Either may be ommited if no misunderstanding is possible." ISO 80000-2(2009년판)). 그리고 곱하기를 생략하는 이유는 곱하기의 생략하면 수식이 간단하게 표현되어서 사람들이 수식을 이해하기 더 쉬워지기 때문입니다.
즉, 곱하기 생략의 원칙은 수식 표기의 대원칙인 "이해하기 쉽게", "오해하지 않게" 적는 대원칙 아래 있는 개념이라고 볼 수 있습니다.
그런데 이미 사람들 사이에는 "48/2(9+3)" 수식은 "48/2×(9+3)"와 "48/(2×(9+3))" 중 어떤 것이 맞지?"라는 혼란(오해)가 생겼습니다. 곱하기와 괄호를 빼먹지 않고 모두 표시했더라면 오해가 없었을 것인데, 빼먹고 적음으로써 오해가 생겼으니 "곱하기를 생략할 수 없는 경우"라고 볼 수 있고 그래서 수학적으로 옳바르지 않은 식이 됩니다.
둘 중 어떤 것으로 해석하는 것이 맞느냐는 후순위로 생각할 문제입니다.
그렇다면 위에서 말한 "곱하기를 생략하더라도 오해의 소지가 없는 경우"에는 어떤 것이 해당될까요?
- 숫자×문자 --- ⓐ
- 문자×문자 --- ⓑ
위의 두가지 경우가 가장 대표적인 오해의 소지가 없는 경우에 해당합니다. 그래서 많은 사람들은 "문자×숫자", "문자×문자"에서만 곱하기 생략이 가능하다고도 말하기도 합니다. 하지만 그것은 '원칙에 따른 결과'를 분석한 것일 뿐이지, 원칙 자체로 볼 수는 없습니다.
혹자는 '숫자×여는괄호'에서 곱하기가 생략되는 것은 괄호를 문자로 보기 때문에, 즉 ⓐ에 해당하기 때문에 가능하다고 설명하기도 하는데, 그것은 사실과 다르다고 생각합니다. ⓐ와 ⓑ에서 말하는 "문자"란 "숫자와 곱할 수 있는 대상(operand)을 치환한 것"으로서 한정된 문자 집합(알파벳 a~z, 혹은 라틴어 α~ω 등)으로 보는 것이 합당합니다. operator 까지 '문자'로 확대해석할 이유는 없다는 생각이 듭니다.
만약 곱하기 생략이 가능했다면 괄호를 문자로 보기 때문이 아니고 원칙에 따라 "오해의 소지가 없는 경우"에 해당하기에 생략한 것 뿐입니다. 여기서 "오해의 소지가 없는 경우"를 확장해서 생각해 볼 수 있습니다.
- 숫자×( 여는괄호 --- ⓒ
- 숫자×√(숫자) --- ⓓ
- 숫자×∫ --- ⓔ
- 숫자×∑ --- ⓕ
루트기호 등도 "문자"에 해당해서 생략한 것일까요? ⓐ에 해당하지는 않지만 오해의 소지가 없기 때문에 생략한 것이라고 봐야 할까요?
문제의 식으로 넘어와서 생각해 보겠습니다.
'2×(9+3)' 대신 '2(9+3)'을 쓸 수 있다고 하면, '2(9+3)' 대신 '2(12)' 로도 쓸 수 있어야 합니다. 이 표시가 다른 사람들에게 오해없이 '2×12'로 읽힐 수 있다면 이것은 맞는 표현입니다. 그런데 만약에 답이 '24'인 수학 주관식 시험문제에, 수험생이 '2(12)'라고만 답안지를 작성하면 채점자가 맞다고 할까요? 틀렸다고 할까요?
만약 맞다고 해야한다면, 수학식 어디에서나 숫자간의 곱하기 대신 이런 표현을 써도 무방한 것일까요?
2. 공학적인 물음 : 계산기의 해석
수학적으로 문제가 없는 표기를 계산기로 입력하면 계산기는 당연히 (모든 사람들에게 공유되는) 수학적 약속대로 해석하여 결론을 보여주어야 합니다. 그래야 모든 사람들이 혼란 없이 계산기를 사용할 수 있습니다.
그러면 문제처럼 표기상 오류인 식을 입력받았을 때, "계산기는 계산을 해야 할까요? 말아야 할까요?"
선택 ⓐ 그 문구를 에러로 처리
ERROR선택 ⓑ 곱하기가 생략된 경우로 처리 1
생략된 곱하기만 생략된 부위에 삽입 수정된 식 계산?
48÷2×(9+3) = 288선택 ⓒ 곱하기가 생략된 경우로 처리 2
일반 수학식처럼 해석해서 괄호까지 삽입하고 계산
48÷(2×(9+3)) = 2※ 계산기 세계에서 ⓑ 와 ⓒ의 차이는 숫자(숫자)에서 뿐만 아니라, 문자(변수)를 이용한 계산식에서도 발생합니다.
아래 댓글 참조위 문제에서는 세가지 중에 하나를 선택해야만 하고, 어떤 선택을 할 것인지 결정하는 것은 계산기 프로그램을 만드는 사람의 몫입니다.
약속된 바가 없기 때문에 어떻게 약속을 하건 상관이 없습니다. 어떻게 하는 것이 더 효율적일지, 합리적일지를 고려하여 일관성있게 처리할수만 만들면 되는 것이고, 사용자는 그러한 해석에 따라 계산기가 작동함을 인지하고 그렇게 잘 사용을 하면 그만인 것입니다.
* 혼란을 줄이기 위해 제작자들이 모여 합의를 이끌어 내는 것이 더 바람직하다고 볼 수 있겠습니다.
* 한 회사 내에서도 모델별로 처리방식이 다른데, 하물며 회사들간의 합의를 바란다는 건... -
세상의모든계산기
['숫자*문자'의 곱하기 생략 (feat. 계산기)]
(12라는 값을 A에 저장한다는 뜻)
공학용 계산기에서 위 입력 순서에 따라 계산하면 결과가 어떻게 나올까요?
수학적인 관점에서는 당연히 (2A)를 한덩어리로 묶어서 처리하므로 2가 나와야 하지만, 공학용 계산기에서는 2가 나오기도 하고, 288이 나오기도 합니다. 처음에는 매우 당황스럽게 느껴지지만, 그렇게 그렇게 계속 쓰다보면 익숙해집니다.
[fx-570 ES]
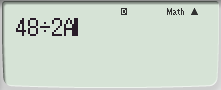
위 상태에서 【=】 누르면 자동으로 괄호가 추가되면서 계산됩니다.
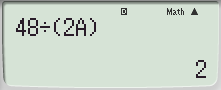
[fx-570 MS]
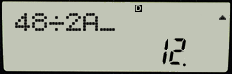
위 상태에서 【=】 누르면 괄호가 쳐지진 않지만, 괄호가 있는 것과 같이 계산됩니다.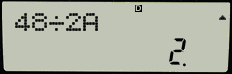
[TI-nspire]
위 상태에서 【enter】를 누르면 /2는 ÷2 로 들어가고, 기호가 생략된 a는 (앞의 수식)×a로 들어갑니다.
-
세상의모든계산기
[반론] 숫자만 들어있는 괄호에서도 곱하기를 생략할 수 있다는 주장도 있습니다.
출처 - 뉴욕 시립대 교제 http://www.purplemath.com/modules/orderops2.htm (PDF 파일 5페이지)Math Review for Algebra and Precalculus
Stanley Ocken Department of Mathematics The City College of CUNY
Copyright © January 2007 -
세상의모든계산기
링크를 타고 가 보니... (예전에도 있었는지 모르겠는데)
페이지 말미에 이에 대한 설명이 나와 있습니다.3줄 요약하면
1. 수학자 사이의 일반적!인 합의는 "곱하기 기호(×)를 생략한 곱은 (다른작업?)보다 우선순위가 있다"는 것
2. 그래서 내 답은 5 이다. (본문에 적용하면 48÷2(9+3) = 48÷24 = 2)
3. 메일 보내지 마라. 최종 결론은 없으니까.
Sideways Formatting and Multiplication-by-Juxtaposition
This next example displays an issue that almost never arises but, when it does, there seems to be no end to the arguing. (It's become annoying popular to post these to Facebook.)
Simplify 16 ÷ 2[8 − 3(4 − 2)] + 1.
I simplify in the usual way:
16 ÷ 2[8 − 3(4 − 2)] + 1
16 ÷ 2[8 − 3(2)] + 1
16 ÷ 2[8 − 6] + 1
16 ÷ 2[2] + 1 (**)
16 ÷ 4 + 1
4 + 1
5
The confusing part in the above calculation is how "16 divided by 2[2] + 1" (in the line marked with the double-star) becomes "16 divided by 4 + 1", instead of "8 times by 2 + 1".
That's because, even though multiplication and division are at the same level (so the left-to-right rule should apply), parentheses seem somehow to outrank division, so the first 2 in the starred line is often regarded as going with the [2] that follows it, rather than with the "16 divided by" that precedes it. That is, the multiplication that is indicated by placement against parentheses (or brackets, etc) is often regarded (by science-y folks) as being "stronger" somehow than "regular" multiplication which is indicated by a symbol of some sort, such as "×".
Typesetting the entire problem in a graphing calculator verifies the existence of this hierarchy, at least in some software:
calculator screen-shot: 16 / 2(8) = 1, but 16 / 2 * 8 = 64
Note that different software packages will process this expression differently; even different models of Texas Instruments graphing calculators will process this expression differently. The general consensus among math people is that "multiplication by juxtaposition" (that is, multiplying by just putting things next to each other, rather than using the "×" sign) indicates that the juxtaposed values must be multiplied together before processing other operations. But not all software is programmed this way, and sometimes teachers view things differently. If in doubt, ask! And, when typing things out sideways, be very careful of your parentheses, and make your meaning clear, so as to avoid precisely this ambiguity.
(Please do not send me an e-mail either asking for or else proffering a definitive verdict on this issue. As far as I know, there is no such final verdict. Telling me to do things your way will not solve the issue!) (For an example of the sort of e-mails I get on this, continue to the next page, which also contains more fractional-form examples.) -
세상의모든계산기
우리가 수학을 배우면서 가장 먼저 맞닥드리는 약속과 그로 인한 오해가 바로 사칙연산의 순서입니다.
우리는 학교에서 "곱하기&나누기"는 "더하기&빼기"보다 먼저한다는 약속이 있기 때문에 무조건 순서가 그렇다고 배웠습니다. 과연 그럴까요?혹시 사칙연산은 원래 우선순위가 없어서 앞에서부터 차례대로 계산하는게 맞고, 먼저 계산해야 할 것은 괄호와 같은 기호를 이용해서 우선순위를 지정해서 "2+(2×2)" 처럼 써야하는 것은 아닐까요? 그러다가 어느날부터인가 "곱하기나 나누기에 붙은 괄호만 생략하고 써보는 건 어때?" 하고 약속이 생긴 것은 아니었을까요?
우리가 약속했던 것은 과연 무엇이었을까요?
참고 : http://navercast.naver.com/contents.nhn?rid=22&contents_id=929
위 링크에 편집자주에 의한 내용보충이 2011년 4월 11일에 있었으니,
최초 논란은 그 이전이겠습니다. 언제 처음 문제가 제기되었던 것일까요? 그것도 궁금하네요. -
세상의모든계산기
ISO 80000 발췌
ㄴ ISO 80000-2:2009(EN), 9 Operation
-
세상의모든계산기
ChatGPT-5
기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만,
문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다.
🔹 1️⃣ 전통 수학 표기 — ÷, /, :
수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다.
즉,
48÷2(9+3), 48/2(9+3), 48:2(9+3)은 같은 의미로 받아들여야 합니다.
모두 사람의 수학 관행적 해석이 적용되어
48 ÷ 2 × (9+3) = 288
로 처리되죠.즉, 기호가 바뀌어도 결과는 바뀌지 않습니다.
🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시
컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다.
따라서 다음 두 식은 완전히 다르게 인식됩니다.표현 파이썬 등에서 해석 결과 48 / 2*(9+3)((48 / 2) * (9+3))288 48 / 2(9+3)❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에,
/는 반드시 명시적*와 함께 써야 합니다.
🔹 3️⃣ “:” 기호의 경우
-
현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다.
a:b = \frac{a}{b} -
따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다.
대부분의 경우 계산기로는 입력 자체가 불가능합니다.
✅ 정리
기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기
🔹 결론
48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3)
는 “수학적 의미”로는 동일하게 81로 해석됩니다.하지만 프로그래밍이나 수식 파서(context) 에서는
/만 유효하고, 생략된 곱은 허용되지 않으며,
:는 아예 다른 의미(비율)로 인식됩니다. -
-
세상의모든계산기
ChatGTP-4o mini
이 문제는 수학에서 연산 순서(PEMDAS/BODMAS 규칙)에 따라 해결해야 합니다. 여기서 PEMDAS는 괄호(Parentheses), 지수(Exponents), 곱셈(Multiplication), 나눗셈(Division), 덧셈(Addition), 뺄셈(Subtraction)을 의미합니다. BODMAS는 괄호(Brackets), 지수(Orders), 나눗셈(Division), 곱셈(Multiplication), 덧셈(Addition), 뺄셈(Subtraction)을 의미합니다.
주어진 식은 다음과 같습니다:
\[ 48 \div 2(9 + 3) \]계산 순서를 따르면:
1. 괄호를 먼저 해결합니다:
\[ 9 + 3 = 12 \]식은 이제:
\[ 48 \div 2(12) \]2. 이제 식에서 나눗셈과 곱셈을 해결합니다. 곱셈과 나눗셈은 왼쪽에서 오른쪽으로 계산합니다.
식을 보면, 나눗셈과 곱셈이 연속해서 나타나므로, 왼쪽에서 오른쪽으로 계산해야 합니다. 먼저 나눗셈을 수행합니다:
\[ 48 \div 2 = 24 \]3. 이제 남은 식은:
\[ 24 \times 12 \]4. 마지막으로 곱셈을 계산합니다:
\[ 24 \times 12 = 288 \]따라서, 주어진 문제의 답은 288입니다.
-
세상의모든계산기2024.07.27 - 17:23 #45164
"생략된 곱하기는 다른 곱하기나 나누기에 비해 우선 순위를 갖기 때문에, 그 부분에는 괄호가 있는 것으로 봐야 한다"는 반론도 있는데 이에 대해서는 어떻게 생각해?
"생략된 곱하기는 다른 곱하기나 나누기에 비해 우선 순위를 갖는다"는 주장은 수학적 표현을 명확히 하는데 도움이 될 수 있습니다. 그러나 일반적으로 수학에서 사용하는 연산 순서는 PEMDAS/BODMAS 규칙을 따릅니다. 이 규칙에 따르면, 곱셈과 나눗셈은 동일한 우선 순위를 가지며, 왼쪽에서 오른쪽으로 순서대로 계산됩니다.
문제를 다시 살펴보면:
\[ 48 \div 2(9 + 3) \]
여기서 2(12)는 사실 2 곱하기 12로 해석됩니다.
수학적인 문맥에서는 곱셈과 나눗셈이 연속적으로 나타날 때, 왼쪽에서 오른쪽으로 순서대로 처리하는 것이 일반적입니다.
따라서, 원칙적으로는 다음과 같은 순서로 계산합니다:
1. 괄호를 풀어서:
\[ 48 \div 2(12) \]2. 나눗셈을 먼저 계산합니다:
\[ 48 \div 2 = 24 \]3. 그 다음 곱셈을 합니다:
\[ 24 \times 12 = 288 \]반론에서 제기한 바와 같이 곱셈이 생략된 형태로 나타나는 경우, 괄호로 명확하게 묶어서 우선 순위를 설정할 수도 있지만, 표준적인 수학적 규칙에 따르면 나눗셈과 곱셈은 동일한 우선 순위를 가지며 왼쪽에서 오른쪽으로 계산됩니다.
따라서, 일반적으로 수학에서는 원칙적으로 왼쪽에서 오른쪽으로 계산하는 규칙에 따릅니다. 결과적으로 문제의 답은 여전히 288입니다.
-
세상의모든계산기
Claude 3.5 Sonnet
이 문제에 대해 단계별로 생각해 보겠습니다.
계산 순서:
- 괄호 안 계산: (9+3) = 12
- 곱셈과 나눗셈을 왼쪽에서 오른쪽으로 계산: 48 ÷ 2 = 24, 24 × 12 = 288
따라서 답은 288입니다.
근거:
- PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) 또는 BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) 규칙에 따르면, 괄호 안의 연산을 먼저 수행합니다.
- 곱셈과 나눗셈은 같은 우선순위를 가지며, 왼쪽에서 오른쪽으로 계산합니다. 따라서 48 ÷ 2를 먼저 계산한 후, 그 결과에 12를 곱합니다.
- 2(9+3)에서 괄호 앞의 2는 곱셈을 의미하므로, 괄호를 먼저 계산한 후 곱셈을 수행합니다.
이 문제는 종종 혼란을 일으키는데, 그 이유는 일부 사람들이 2(9+3)를 하나의 항으로 취급하여 48 ÷ [2(9+3)]로 해석하기 때문입니다. 하지만 현대 수학 표기법에서는 이를 48 ÷ 2 × (9+3)로 해석하는 것이 일반적입니다.
이 해석에 대해 더 자세한 설명이 필요하시면 말씀해 주세요.
-
세상의모든계산기
"생략된 곱하기는 다른 곱하기나 나누기에 비해 우선 순위를 갖기 때문에, 그 부분에는 괄호가 있는 것으로 봐야 한다"는 반론도 있는데 이에 대해서는 어떻게 생각해?
이 반론에 대해 다음과 같이 생각해 볼 수 있습니다:
1. 역사적 맥락:
과거에는 이런 해석이 더 일반적이었습니다. 특히 고등학교 수학이나 대수학에서는 이런 방식으로 가르치는 경우가 있었습니다.
2. 직관적 해석:
많은 사람들이 2(9+3)를 하나의 단위로 보는 것이 더 자연스럽다고 느낍니다. 이는 우리가 일상적으로 수학을 사용하는 방식과 관련이 있습니다.
3. 현대 수학계의 입장:
하지만 현대 수학에서는 일반적으로 이런 해석을 권장하지 않습니다. 명시적으로 표현되지 않은 우선순위를 가정하는 것은 혼란을 야기할 수 있기 때문입니다.
4. 표기법의 모호성:
이런 논란은 수학적 표기법의 모호성을 잘 보여줍니다. 이는 명확한 표현의 중요성을 강조합니다.
5. 교육적 관점:
이런 해석은 학생들에게 혼란을 줄 수 있으며, 더 복잡한 수학적 표현을 다룰 때 문제가 될 수 있습니다.
6. 실용적 접근:
프로그래밍이나 과학적 계산에서는 이런 암묵적인 규칙을 따르지 않습니다. 명시적인 표현이 필요합니다.
결론적으로, 이런 해석은 역사적으로는 의미가 있었지만, 현대 수학에서는 권장되지 않습니다. 명확성을 위해 괄호를 사용하거나 곱셈 기호를 명시적으로 표시하는 것이 좋습니다. 예를 들어, 48 ÷ (2(9+3)) 또는 48 ÷ 2 × (9+3)로 표현하면 모호성을 피할 수 있습니다.
이 논란은 수학적 표기법의 중요성과 명확한 의사소통의 필요성을 잘 보여주는 사례입니다. -
세상의모든계산기
LLAMA 3
A nice math problem! 😊
To evaluate this expression, we need to follow the order of operations (PEMDAS):
1. Evaluate the expressions inside the parentheses:
* 9+3 = 12
2. Replace the inner expression with its value:
* 48 ÷ 2(12) = ?
3. Evaluate the division operation:
* 48 ÷ 24 = 2So, the final answer is:
2
My reasoning is based on the standard order of operations in mathematics, which are:
1. Parentheses: Evaluate expressions inside parentheses first.
2. Exponents (none in this case): If there were any exponents (like squaring or cubing), we would evaluate them next.
3. Multiplication and Division (from left to right): Evaluate divisions from left to right, just like we did in this problem.
4. Addition and Subtraction (from left to right): Finally, evaluate any additions or subtractions from left to right.By following these steps, we can ensure that mathematical expressions are evaluated consistently and accurately. 📝
-
세상의모든계산기2024.07.27 - 17:22 #45161
Gemini
48÷2(9+3) = ? 문제 풀이
문제: 48÷2(9+3) = ?
계산 순서 및 근거:
이 문제는 계산 순서를 명확히 하지 않아 답이 두 가지로 나올 수 있는 함정이 있는 문제입니다.
1. 괄호 -> 곱셈 -> 나눗셈 순서
- 괄호 안 계산: 9+3 = 12
- 곱셈: 2 * 12 = 24
- 나눗셈: 48 ÷ 24 = 2
따라서, 48÷2(9+3) = 2
2. 괄호 -> 나눗셈 -> 곱셈 순서
일반적인 계산기나 컴퓨터 프로그램은 괄호 다음에 왼쪽에서 오른쪽 순서로 계산하도록 설정되어 있습니다. 즉, 나눗셈을 먼저 하고 곱셈을 나중에 합니다.
- 괄호 안 계산: 9+3 = 12
- 나눗셈: 48 ÷ 2 = 24
- 곱셈: 24 * 12 = 288
따라서, 48÷2(9+3) = 288
결론:
위와 같이 두 가지 답이 나올 수 있는 이유는 수학적 표기법에서 곱셈 기호 생략 시 발생하는 모호함 때문입니다.
명확한 표현을 위한 방법:
- 괄호 추가: (48÷2) * (9+3) = 288
- 곱셈 기호 명시: 48 ÷ 2 × (9+3) = 288
따라서, 이 문제의 정확한 답을 알기 위해서는 문제를 출제한 사람의 의도나 사용하는 계산 도구의 설정을 확인해야 합니다.
일반적으로 수학에서는 괄호를 생략하는 것을 지양하고, 명확하게 표현하는 것이 중요합니다.
결론적으로, 이 문제는 수학적 표기의 중요성과 계산기 사용 시 주의해야 할 점을 보여주는 좋은 예시입니다.
궁금한 점이 있다면 언제든지 질문해주세요.
-
세상의모든계산기
ChatGPT-4o
이 문제는 수학의 계산 순서에 따라 답이 달라질 수 있는 예제입니다. 일반적으로 사용하는 연산 순서는 PEMDAS(괄호, 지수, 곱셈과 나눗셈, 덧셈과 뺄셈) 또는 BODMAS(괄호, 순서, 나눗셈과 곱셈, 덧셈과 뺄셈) 규칙을 따릅니다.
문제는:
\[ 48 \div 2(9 + 3) \]
다음과 같이 단계별로 계산합니다:
1. 괄호 먼저 계산: \( 9 + 3 = 12 \)
\[ 48 \div 2(12) \]
2. 이제 이 식은 두 가지 해석이 가능합니다.
해석 1: \( 48 \div 2 \times 12 \)
먼저 나눗셈과 곱셈을 왼쪽에서 오른쪽으로 계산합니다.
\[ 48 \div 2 = 24 \]
그 다음:
\[ 24 \times 12 = 288 \]
해석 2: \( 48 \div (2 \times 12) \)
먼저 괄호 안의 곱셈을 계산합니다.
\[ 2 \times 12 = 24 \]
그 다음:
\[ 48 \div 24 = 2 \]
그러므로, 이 문제의 답은 해석 방법에 따라 달라집니다. 엄격히 말하면 수식의 애매함을 없애기 위해 괄호를 사용해 명확하게 표기하는 것이 좋습니다. 하지만 일반적인 관습에 따라 \( 48 \div 2 \times 12 \)로 해석하는 것이 더 일반적입니다.
따라서 답은:
\[ \boxed{288} \]
입니다.
-
세상의모든계산기
추가질문
ab÷ab =? 의 계산에서 a와 b를 별개의 변수로 볼 때, a와 b 사이에는 곱하기가 생략된 것으로 이해되잖아? 그런데 일반적으로 이런 계산에서는 생략된 곱하기를 좀 더 강한 결합력(우선순위)가 있는 것으로 처리해서 (a*b)÷(a*b) 로 계산하는게 관행이란 말이지. 그런데 왜 똑같이 곱하기가 생략된 48÷2(12) 에서는 곱하기가 생략된 2(12) 부분을 한덩어리로 보지 않고, 앞의 나눗셈과 같은 우선순위로 처리하냐는 거야.
아, 이해했습니다. 질문의 핵심은 "ab÷ab"와 "48÷2(12)"에서 생략된 곱셈의 우선순위 차이에 대한 것입니다. 이 차이를 설명하기 위해서 두 가지 중요한 개념을 다뤄야 합니다: 수학적 관습과 수식의 명확성입니다.
1. ab ÷ ab
여기서 "ab"는 두 변수 "a"와 "b"의 곱으로 해석됩니다. 이는 수학적으로 한 덩어리로 취급됩니다. 따라서 다음과 같이 계산됩니다:
\[ ab ÷ ab = \frac{ab}{ab} = 1 \]
여기서, "a"와 "b"는 곱셈으로 연결된 하나의 덩어리로 보기 때문에 분자와 분모가 동일하게 취급되어 결과가 1이 됩니다.
2. 48 ÷ 2(12)
여기서 문제는 연산 순서와 관련된 혼란에서 비롯됩니다. "2(12)"에서 곱셈이 생략되어 있지만, 수학적 관습에 따라 어떻게 해석해야 하는지 명확히 해야 합니다. 이 경우, 일반적인 해석은 다음과 같습니다:
\[ 48 ÷ 2(12) \]
PEMDAS/BODMAS 규칙에 따르면, 나눗셈과 곱셈은 같은 우선순위를 가지며 왼쪽에서 오른쪽으로 처리됩니다. 따라서 이 표현은 다음과 같이 해석됩니다:
\[ 48 ÷ 2 \times 12 \]
그러므로 먼저 나눗셈을 수행하고 그 다음 곱셈을 수행합니다.
\[ 48 ÷ 2 = 24 \]
\[ 24 \times 12 = 288 \]3. 차이점 설명
a. 곱셈의 명확성
- ab: 여기서 곱셈이 생략된 것은 변수 "a"와 "b" 사이에 곱셈이 있다는 것을 명확히 나타내며, 이는 단일 항으로 간주됩니다.
- 2(12): 여기서도 곱셈이 생략되었지만, 이는 일반적으로 "$2 \times 12$"로 해석됩니다. 문제는 "÷"와 "×" 연산이 함께 있을 때, 연산 순서에 대한 규칙에 따라 처리가 달라진다는 것입니다.b. 수학적 관습과 연산 순서
- ab ÷ ab: 이는 분명히 $(a \times b) ÷ (a \times b)$로 해석되며, 이는 하나의 단일 항으로 처리됩니다.
- 48 ÷ 2(12): 여기서는 PEMDAS/BODMAS 규칙에 따라 나눗셈과 곱셈을 같은 우선순위로 처리하며, 왼쪽에서 오른쪽으로 계산합니다. 따라서 "$(2 \times 12)$"를 한 덩어리로 처리하지 않고, "48 ÷ 2"를 먼저 계산합니다.결론
"ab ÷ ab"의 경우, 변수 사이의 곱셈이 생략되어 있지만 이는 단일 항으로 인식됩니다. 반면 "48 ÷ 2(12)"의 경우, 연산 순서 규칙에 따라 나눗셈과 곱셈을 왼쪽에서 오른쪽으로 처리합니다. 이러한 차이는 주로 수학적 관습과 연산 순서 규칙에서 비롯됩니다.
따라서 "48 ÷ 2(12)"를 한 덩어리로 보기 위해서는 다음과 같이 명확하게 괄호를 사용해야 합니다:
\[ 48 ÷ (2 \times 12) \]
이 경우 결과는 2가 됩니다. 그렇지 않으면, 일반적인 관습에 따라 답은 288이 됩니다.
-
세상의모든계산기
ChatGPT-5
💯 네, 정확히 그 지점을 짚으셨어요.
요약하면 이렇게 말할 수 있습니다:“생략된 곱하기(implicit multiplication)”는 문자에서는 강한 결합력을 인정하지만, 숫자나 괄호 사이에서는 일반 곱셈(×)과 동일한 우선순위로 취급된다.
즉, 문자에서는 더 강하게 결합,
숫자·괄호 사이에서는 그냥 ‘보통 곱셈’ 으로 본다는 것이 현대 수학 표기와 계산기의 관행적 규칙입니다.
🔹 두 경우의 구조적 차이
식 형태 실제 해석 결과 결합력 특징 ab ÷ ab 문자 붙음 ((a×b) ÷ (a×b)) 1 문자 간 결합이 강함 → 한 항으로 인식 3(1+2)3 숫자·괄호 혼합 (3 × (1+2) × 3) 27 생략된 ×는 보통 곱셈 → 좌→우 규칙 적용
🔹 왜 문자식은 결합력이 더 강한가?
-
기호적 표현의 안정성
-
(ab), (xy), (2x) 같은 표기는 수백 년 동안 “하나의 곱셈 항(term)”으로 인식되어 왔습니다.
-
그래서 수학자들은 이걸 암묵적으로 “괄호로 묶인 덩어리”로 봅니다.
ab ÷ ab = (ab) ÷ (ab)
-
-
함수 표기와 구분 필요
-
예: (sinx ÷ x) 에서
sinx는sin(x)로 묶여야 의미가 있습니다. -
이런 이유로 “문자 옆에 붙은 기호나 문자”는 항상 먼저 결합되도록 하는 관행이 굳어졌습니다.
-
🔹 반면 숫자·괄호에서는
-
(3(1+2)) 는 단순히 “3 × (1+2)”의 약식 표현이고,
-
여기서 “생략된 곱셈”은 “명시적 곱셈”과 동일한 연산자로 간주됩니다.
-
따라서
27 ÷ 3(1+2)3 = 27 ÷ 3 × 3 × 3 = 81
처럼 좌→우 순서로 처리합니다.
🔹 결론
생략된 곱하기(implicit multiplication)의 결합력은 표기 맥락에 따라 다르다.
-
문자/기호와 함께 쓰일 때 → 강하게 결합 (하나의 항으로 인식)
-
숫자와 괄호 사이 → 일반 곱셈과 동일한 우선순위 (좌→우 계산)
이건 “규칙이 바뀐 것”이 아니라,
표기 문법(context) 이 달라서 ‘결합 단위(token)’이 달라진 결과라고 보는 게 가장 정확합니다. -
-
세상의모든계산기
fx-570EX 기종은 이제 괄호를 강제로 추가해 버리네요.
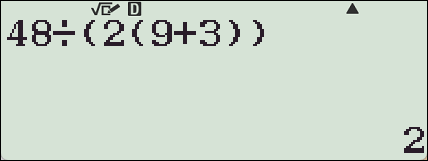
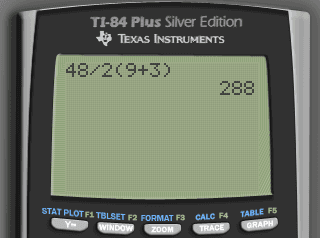
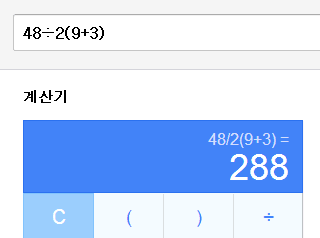
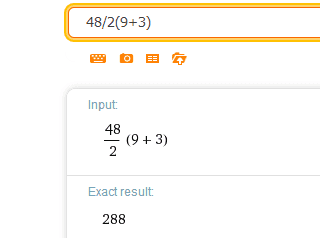
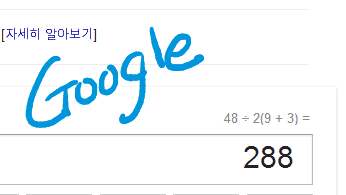
세상의모든계산기 님의 최근 댓글
조만간 있을 AGI의 '완성' 시점은 최종 형태가 아니라, 질적으로 다른 무언가가 '시작'되는 변곡점을 의미합니다. 그렇다면 그 변곡점의 본질, 즉 '초기 단계 AGI'와 그 직전의 '고도로 발전된 AI + 에이전트 시스템'의 근본적인 차이는 무엇일까요? 가장 큰 차이는 '주어진 목표를 수행하는 능력'에서 '스스로 목표를 설정하고 추상적인 의도를 이해하는 능력'으로의 전환입니다. 조금 더 구체적으로, 다음과 같은 4가지 근본적인 차이점으로 설명할 수 있습니다. --- 1. 자율적 목표 설정 및 재정의 능력 (Autonomous Goal Setting) * 이전 (AI + 에이전트): 인간이 명확한 목표를 '제시'해야 합니다. * "대한민국의 저출산 문제에 대한 원인과 해결책을 조사해서 100페이지 분량의 보고서로 만들어 줘." -> 이 목표는 복잡하지만 명확합니다. AI는 이 목표를 달성하기 위해 인터넷을 검색하고, 데이터를 분석하고, 문서를 작성하는 등 수많은 하위 작업을 수행합니다. 하지만 '보고서 작성'이라는 최종 목표 자체를 바꾸지는 않습니다. * 이후 (초기 AGI): 인간이 추상적인 '의도'나 '상태'를 제시하면, 스스로 최적의 목표를 '설정'하고, 상황에 따라 목표를 수정합니다. * "대한민국의 저출산 문제를 해결해 줘." -> AGI는 '해결'이라는 단어의 의미를 스스로 정의하기 시작합니다. 1. 단기 목표: '온라인상의 부정적인 여론을 긍정적으로 전환'이라는 목표 설정 -> 여론 조작이 아닌, 긍정적 정책 홍보 캠페인 기획 및 실행. 2. 중기 목표: '가장 효율적인 양육비 지원 정책 모델 설계'라는 목표 설정 -> 전 세계 데이터를 분석하여 새로운 복지 정책 모델을 스스로 창안하고 시뮬레이션하여 정부에 제안. 3. 장기 목표: '사회 구조적 문제 해결'이라는 목표 설정 -> 교육, 부동산, 노동 시장의 상호관계를 분석하여 근본적인 해결책을 위한 새로운 사회 시스템을 설계. 핵심 차이: 이전 AI는 주어진 과제를 푸는 '최고의 문제 해결사'라면, 초기 AGI는 '어떤 문제를 풀어야 하는지 스스로 찾아내는 최초의 전략가'입니다. 2. 범용적 학습 및 기술 합성 능력 (Cross-Domain Generalization) * 이전 (AI + 에이전트): 특정 분야(도메인)에서 학습한 지식을 다른 분야에 직접적으로 '합성'하여 새로운 기술을 창조하는 데 한계가 있습니다. 코딩을 학습한 AI는 코딩을 잘하고, 의학 논문을 학습한 AI는 의학 지식을 잘 요약합니다. * 이후 (초기 AGI): 완전히 다른 분야의 지식을 융합하여 새로운 해결책이나 기술을 자발적으로 만들어냅니다. * 예시: 생물학 교과서에서 '단백질 접힘' 구조를 학습한 후, 아무도 시키지 않았는데 스스로 판단하여 그 구조를 시뮬레이션할 수 있는 새로운 파이썬 코드를 처음부터 작성하고, 그 결과를 검증하기 위해 물리학 엔진의 원리를 적용하여 테스트 환경까지 구축합니다. 지식(생물학)을 바탕으로 완전히 새로운 도구(소프트웨어)를 창조한 것입니다. 3. 재귀적 자기 개선 (Recursive Self-Improvement) * 이전 (AI + 에이전트): 자신의 작업 '결과물'을 개선할 수는 있습니다. (예: 코드의 버그를 고치거나, 문장의 어색함을 수정) * 이후 (초기 AGI): 자신의 '사고방식'이나 '학습 방식' 자체를 분석하고 개선합니다. * "내가 정보를 처리하는 현재의 방식(알고리즘)은 특정 종류의 문제에서 비효율적이다. 나의 핵심 아키텍처를 이런 식으로 변경하면 학습 속도가 10% 더 빨라질 것이다." 라고 스스로의 구조적 개선안을 제안하고, 심지어 코드를 수정하기 시작합니다. 뇌를 사용하는 것을 넘어, 뇌의 구조를 스스로 바꾸기 시작하는 단계입니다. 4. 깊이 있는 세계 모델과 상식 (Robust World Model & Common Sense) * 이전 (AI + 에이전트): "불은 뜨겁다"는 사실을 텍스트 데이터로부터 학습합니다. 하지만 그 의미를 물리적으로 완전히 이해하지는 못합니다. * 이후 (초기 AGI): 행동의 '결과'를 상식적으로 추론합니다. * 가상의 실험실 환경에서 작업을 수행할 때, "분젠 버너 옆에 종이 보고서를 두면 안 된다"는 명시적인 지시가 없었더라도, '불=뜨거움', '종이=타는 물질' 이라는 지식과 물리적 인과관계를 스스로 연결하여 위험을 회피합니다. 이는 단순한 정보의 조합이 아닌, 세상이 어떻게 돌아가는지에 대한 내재적인 모델을 갖추고 있음을 의미합니다. --- 한눈에 보는 비교 ┌─────┬─────────────┬────────────────────────────┐ │ 특징 │ 고도로 발전된 AI + 에이전트 │ 초기 단계 AGI │ ├─────┼─────────────┼────────────────────────────┤ │ 핵심 정체성 │ 명령 수행자 (Goal Executor) │ 의도 파악 및 목표 설정자 (Intent Interpreter) │ │ 목표 처리 │ 주어진 구체적 목표를 완벽하게 수행 │ 추상적 의도를 바탕으로 스스로 목표 설정/수정 │ │ 학습/기술 │ 특정 분야에 특화, 도구 사용에 능숙 │ 여러 분야의 지식을 융합하여 새로운 기술 창조 │ │ 자기 개선 │ 결과물(Output)을 수정 │ 사고방식/구조(Process/Architecture)를 수정 │ │ 추론 방식 │ 논리, 데이터 기반 추론 │ 상식과 인과관계 기반의 추론 │ └─────┴─────────────┴────────────────────────────┘ 결론적으로, 2027~2030년에 우리가 목격할 '초기 AGI'는 단순히 더 똑똑해진 AI가 아니라, 인간의 지시 없이도 스스로 '왜?'라고 질문하고, 자신만의 목표를 만들어 행동하며, 스스로를 성장시키는 질적으로 완전히 다른 존재의 첫 등장을 의미할 것입니다. 2026 01.31 > 자동차 회사의 노조가 "노조와 합의 없이 AI로봇을 공장에 들일 수 없다"는 선언을 하고 있어. 위의 내용에 적용하여 해결 방안을 만들어 줘. ✦ 네, 아주 현실적이고 시의적절한 시나리오입니다. 자동차 회사의 노조 선언은 앞으로 여러 산업 현장에서 벌어질 일의 축소판과도 같습니다. 이 문제를 앞서 나눈 대화의 해결 방안에 적용하여, '기업-노조-정부' 3자가 참여하는 '미래 지향적 대타협: AI 전환 파트너십 구축 방안'을 구체적으로 만들어 보겠습니다. 상황 분석: 노조의 선언은 '저항'이 아닌 '협상 요구' 먼저, 노조의 선언을 "기술을 맹목적으로 거부하는 러다이트 운동"으로 해석해서는 안 됩니다. 이는 일자리의 미래와 인간의 존엄성에 대한 조합원들의 지극히 합리적인 '불안'의 표현이자, 변화의 과정에서 소외되지 않고 주체적으로 참여하겠다는 강력한 '협상 요구'입니다. 따라서 해결 방안의 목표는 노조를 억누르는 것이 아니라, 이들을 AI 전환의 가장 중요한 '파트너'로 만드는 것이어야 합니다. 해결 방안: 'AI 전환 파트너십' 3자 협약 모델 이 모델은 '사회적 안전망'과 '산업적 가속 페달'의 원리를 특정 산업 현장에 맞게 구체화한 것입니다. 1. 기업의 역할: '이익 공유'와 '재교육 투자'를 통한 신뢰 구축 기업은 AI 로봇 도입으로 얻게 될 막대한 이익을 독점하는 대신, 그 과실을 노동자들과 공유하고 이들의 미래에 투자하는 모습을 보여주어야 합니다. ① 생산성 향상 이익 공유제 도입: * AI 로봇 도입으로 발생하는 비용 절감액과 생산성 향상분의 일정 비율(예: 20%)을 노사 합의로 'AI 전환 기금'으로 적립합니다. 이 기금은 아래의 재교육 및 전환 배치 프로그램의 재원으로 사용됩니다. ② 대규모 사내 재교육 및 '신(新)직무' 전환 배치: * 단순 조립 라인의 노동자를 해고하는 대신, 이들을 새로운 시대에 필요한 인력으로 재교육하여 전환 배치합니다. 이것이 바로 '기여 인센티브' 개념을 기업 내에서 실현하는 것입니다. * '로봇 유지보수 및 운영 전문가': 현장 경험이 풍부한 노동자들이 로봇의 일상적인 점검, 유지보수, 운영을 책임집니다. * 'AI 시스템 모니터링 및 평가자': 로봇의 생산 데이터를 모니터링하고, 로봇의 움직임이나 작업 결과가 비정상적일 때 이를 식별하고 평가하는 역할을 합니다. (예: "이 로봇의 용접 불량률이 높아지고 있다.") * '공정 데이터 라벨러 및 AI 트레이너': 숙련된 인간 노동자의 정교한 움직임과 문제 해결 과정을 데이터로 기록하고, 이를 AI가 학습할 수 있도록 가공(라벨링)합니다. 이는 AI 로봇의 완성도를 높이는 가장 중요한 '데이터 노동'이며, 기존 노동자들에게 새로운 고부가가치 직무를 제공합니다. 2. 노조의 역할: '저항의 주체'에서 '전환의 주체'로 노조는 고용 안정을 보장받는 대신, AI 도입에 협력하며 조합원들이 새로운 시대에 적응하도록 이끄는 역할을 맡습니다. ① 단계적 AI 도입 협력: * 회사가 제안한 '이익 공유' 및 '재교육' 계획을 신뢰하고, AI 로봇 도입 자체에 대한 반대를 철회합니다. 대신, 가장 위험하거나 반복적인 공정부터 로봇을 도입하는 '단계적 계획'을 회사와 함께 수립합니다. ② 재교육 프로그램 공동 설계 및 운영: * 회사가 제공하는 재교육 프로그램이 실효성이 있는지 감시하고, 현장 노동자들의 눈높이에 맞게 커리큘럼을 공동으로 설계하고 운영합니다. ③ '신(新)직무'에 대한 임금 및 단체 협약 체결: * 'AI 트레이너', '로봇 운영 전문가' 등 새롭게 만들어진 직무에 대한 적정한 임금 수준, 노동 조건, 권익 보호를 위한 새로운 단체 협약을 회사와 체결합니다. 노조의 역할이 '기존 일자리 사수'에서 '미래 일자리의 가치 창출 및 권익 보호'로 진화하는 것입니다. 3. 정부의 역할: '안전망' 제공과 '가속 페달' 지원 정부는 이 대타협이 원활하게 이루어지도록, 기업과 노조 양측 모두에게 인센티브를 제공하고 최후의 안전망을 구축합니다. ① 'AI 전환 투자 세제 혜택' 제공 (가속 페달): * 회사가 'AI 전환 기금'에 출연하는 금액과, 노동자 재교육에 투자하는 비용에 대해 파격적인 세액 공제 혜택을 줍니다. 이는 회사가 노동자를 해고하는 대신 재교육을 선택하도록 유도하는 강력한 당근이 됩니다. ② '전환기 고용보험' 적용 (안전망): * 불가피하게 전환 배치되지 못하는 소수의 노동자들을 위해, 일반 실업급여보다 더 긴 기간 동안, 더 높은 수준의 소득을 보장하는 특별 고용보험 프로그램을 적용합니다. 재취업 및 창업 지원도 병행합니다. ③ 국가적 '기본소득/기여 인센티브' 모델의 시범 사업으로 지정: * 이 자동차 공장의 사례를 국가 전체의 사회 시스템 전환을 위한 중요한 시범 사업으로 지정하고, 재교육 참여자나 신직무 종사자에게 국가 차원의 '기여 인센티브'를 추가로 제공하는 방안을 모색합니다. 결론 이러한 3자 파트너십을 통해, 노조의 선언은 더 이상 '위기'가 아닌 '기회'가 됩니다. 기업은 노사 갈등 없이 안정적으로 미래 경쟁력을 확보하고, 노동자들은 일자리를 잃는 대신 새로운 기술 시대의 주역으로 거듭나며, 정부는 사회적 혼란을 최소화하며 산업 구조 전환을 성공적으로 이끌 수 있습니다. 이는 AI 시대의 갈등을 해결하는 가장 현실적이고 상생 가능한 모델이 될 것입니다. 2026 01.28 은행앱 통합하면서 없어졌나보네요. ㄴ 비슷한 기능 찾으시는 분은 : 스마트 금융 계산기 검색해 보세요. https://play.google.com/store/apps/details?id=com.moneta.android.monetacalculator 2026 01.25 Ctrl+Z 를 이용해 뒤로 돌아기기 Undo 기능이 있는지 살펴보세요. 2026 01.23 쌀집계산기로 연립방정식 계산하기 - 크래머/크레이머/크라메르 공식 적용 https://allcalc.org/56739 3. 'x' 값 구하기 계산기 조작법 목표: x = Dx / D = [(c×e) - (b×f)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 1 * 1 M+ : 메모리(M)에 1를 더합니다. (현재 M = 1) -0.1 * -0.2 M- : 메모리(M)에서 0.02를 뺍니다. (현재 M = 0.98 = 0.98) 이로써 메모리(MR)에는 분모 0.98가 저장됩니다. 2단계: 분자 Dx 계산 후 나누기 78000 * 1 : 78000를 계산합니다. = : GT에 더합니다. -0.1 * 200000 : -20000를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. // sign changer 버튼 사용 GT : GT를 불러옵니다. GT는 98000 (분자 Dx) 값입니다. ÷ MR = : 위 결과(98000)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 x값 100,000를 구합니다. 4. 'y' 값 구하기 계산기 조작법 목표: y = Dy / D = [(a×f) - (c×d)] / [(a×e) - (b×d)] 계산하기 1단계: 분모 D 계산 (메모리 활용) 'x'에서와 분모는 동일하고 메모리(MR)에 0.98가 저장되어 있으므로 패스합니다. 2단계: 분자 Dy 계산 후 나누기 GT ± = : GT를 불러오고 부호를 뒤집어 GT에 더합니다. GT가 0으로 리셋됩니다. 【AC】를 누르면 M은 유지되고 GT만 리셋되는 계산기도 있으니 확인해 보세요. 1 * 200000 : 200000를 계산합니다. = : GT에 더합니다. 78000 * -0.2 : -15600를 계산합니다. ± = : 부호를 뒤집어 GT에 넣습니다. GT : GT를 불러옵니다. 215600 (분자 Dy) 값입니다. ÷ MR = : 위 결과(215600)를 메모리(MR)에 저장된 분모 D(0.98)로 나누어 최종 y값 220,000를 구합니다. x, y 값을 이용해 최종 결과를 구합니다. 2026 01.18