Ti nspire cx2 cas 연립방정식 계산 오류
안녕하세요?
계산기의 연립방정식 풀이에 문제가 있는 것 같아 질문을 올립니다.
수식이 길어 나눠서 사진을 찍은 점, 양해 부탁드립니다.
위의 3개의 사진은 삼각함수를 이용하여, 연립방정식을 구성, 아래의 3개의 사진은 삼각함수의 값을 대입하여, 연립방정식을 구성한 것입니다.
삼각함수로 방정식을 구성할 땐, false가 나오나, 값을 입력하면 해가 잘 나옵니다.
이런 경우는 삼각함수로 구성된 방정식을 계산기가 소화하지 못하는 건가요? 아님, 제가 작성한 방정식에 오류가 있는 건가요?
감사합니다.
댓글16
-
-
세상의모든계산기
false 가 아니라 답이 나오게 하려면?
일단 답이 나오게 하는 여러 방법이 있습니다.
1. 인수로서 미지수 결과값 확인을 하나만 하는 방법. 즉 {x,y} 한꺼번에 결과 체크를 하지 않음.
ㄴ 최종 결과값은 x=, y= 이렇게 둘 다 나오긴 합니다.

하지만 나온 결과값(ans)를 원래 식에 넣어보면 양쪽 방정식 모두를 만족(true)시키지 못하고 한쪽은 true 이지만 다른 한 쪽은(false)가 나옵니다.
마지막 경고 마크는 ⚠️"Result obtained using approximate arithmetic." 입니다.
이하 스샷의 경고마크도 모두 같습니다.
-
세상의모든계산기
2. {x,y} 를 인수로 넣으면서 초기 추정값을 넣어도 결과값이 나옵니다.

하지만 이번 결과도 한쪽 방정식만을 만족하였습니다.
-
세상의모든계산기
3. 본문에서 cos, sin 을 풀어서 decimal 형식으로 넣은 것처럼 처리해도 답이 도출됩니다.
개별적으로 입력하지 않더라도, 연립방정식 수식 전체를 approx() 로 씌우면 처리됩니다.

답은 나오지만 이 경우에도 {true, true} 는 나오지 않았습니다.
그런데, 원래의 연립방정식에 검증하면 {true, false} 이지만,
approx() 결과값에 검증하면 {false, true} 로 나오는군요.

-
세상의모든계산기
4. 마지막으로 선형 연립방정식 전문함수인 linsolve() 를 이용해도 답이 나옵니다.
결과값은 {73.049507058478,23.747548955926} 입니다.

이번엔 {true, true} 가 나왔습니다.
* 하지만 아래 댓글 중 '결과값의 비교' 를 보시면 아시겠지만, 그렇게 큰 의미가 있는 것은 아닙니다.
-
세상의모든계산기
답이 잘 나오지 않는 이유?
solve는 답을 찾기 위해 내부적으로 여러 방식을 사용할 수 있습니다.
가장 간단한 방식은 수치적 방법 numerical method 를 이용하는 것이구요.
- 질문자님께서 하신 것처럼 숫자를 대입하거나
- 초기값을 입력하거나
- 계수 등으로 numerical 한 숫자가 들어가거나, 즉 소숫점이 직접 사용되거나
할 때 자동으로 numerical method 로 전환되어 계산됩니다.
그리고 결과에 ⚠️ 를 표시합니다.
그 의미는 적당한 수준(매우 작은 오차 수준)에서 답을 찾았으나,
재수가 없으면 오답일 수 있다는 경고입니다.
따라서 앞으로는
답이 안나올 때는 초기값을 넣는다거나 하는 방식으로 solve를 이용하시면 됩니다.
그럼 처음에 왜 false 가 나왔나를 생각해 보면 두가지 가능성이 있는데
ⓐ numerical method 가 아니라 exact solution 값을 구하려고 했는데 복잡해서 못구했다.
ⓑ numerical method 를 썻지만, 검증해보니 안맞아서 false 로 처리했다.
그런데 ⓑ는 아닌 것 같습니다.
왜냐하면, numerical method 를 사용하면 사소한 오류가 있더라도 ⚠️경고를 할 뿐 무시하고 답을 내놓잖아요?
그럼 ⓐ 가 맞다는 말인데,
지금까지 제가 아는 바로는 입력한 수식에 소숫점이 들어가면 자동으로 approx()처리를 한다고 알고 있었고,
이 solve() 에 방정식 들어가기 전에 (approx) 전처리가 된 것이 들어가니 numerical method로 처리될 줄 알았는데,
아무리 봐도 그게 아닌 것 같습니다. solve에서는 예외적으로 처리가 되는 듯 합니다.
-
세상의모든계산기
각 결과값의 비교
x y {x} 73.049507058553 23.747548955926 {y} 73.049507058479 23.747548955927 {x=1,y=1} 73.049507058477 23.747548955927 approx() 전처리 73.049507058479 23.747548955926 linsolve 73.049507058478 23.747548955926 approx(참 해) 73.049507058547 23.747548955927 * 구해진 x값들은 차이가 비교적 큰데, y값들은 차이가 적은 편입니다.
-
세상의모든계산기
그렇다면 해의 참 값은?
먼저, 모든 decimal 값을 유리수로 변환하고,
solve 로 답을 구함.

변수 x로는 구해지는데 y로는 "Error: Resource exhaustion" 발생 // 이유는 모름.
approx(exsol1)
x=73.049507058547 and y=23.747548955927
-
세상의모든계산기
검증하면
1번 식을 x에 대해 정리하고,
→ 그 x 값을 2번 식에 대입해 넣으면
→ 그 결과로 x는 사라지고 y에 대한 식이 되니, y에 대해 정리하면 참값 y를 얻음.
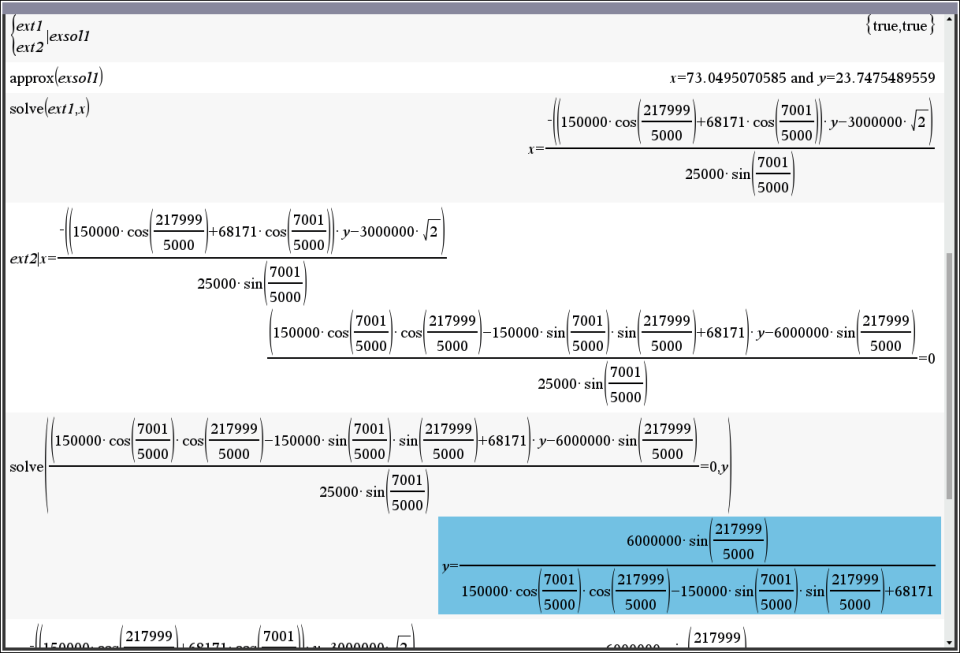
얻은 y의 참값을 처음 x에 대해 정리한 1번식에 대입하면 참 값 x를 얻음.
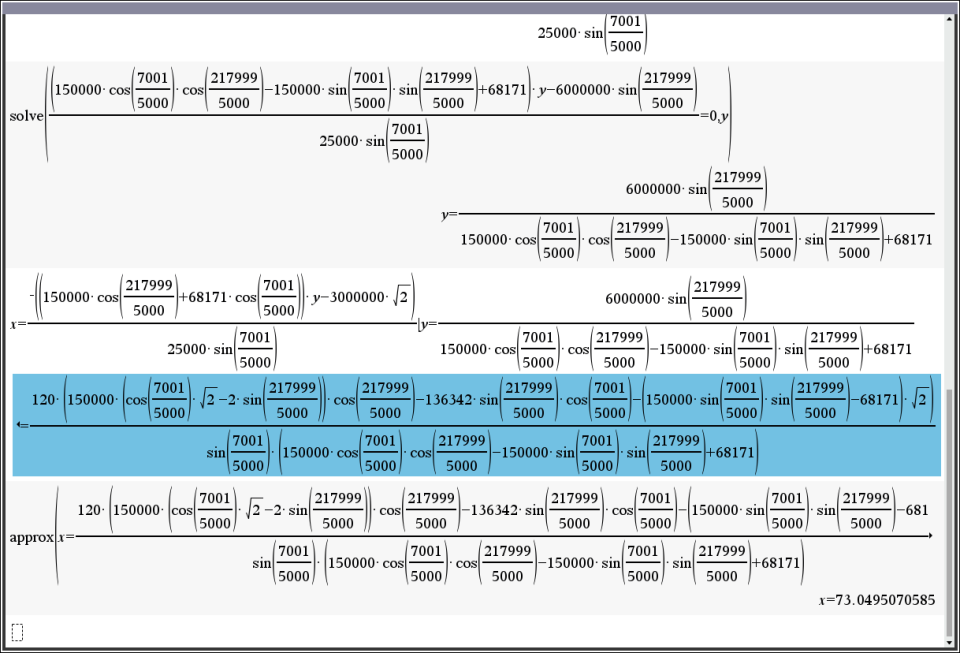
구해진 참값의 근사값을 구하면
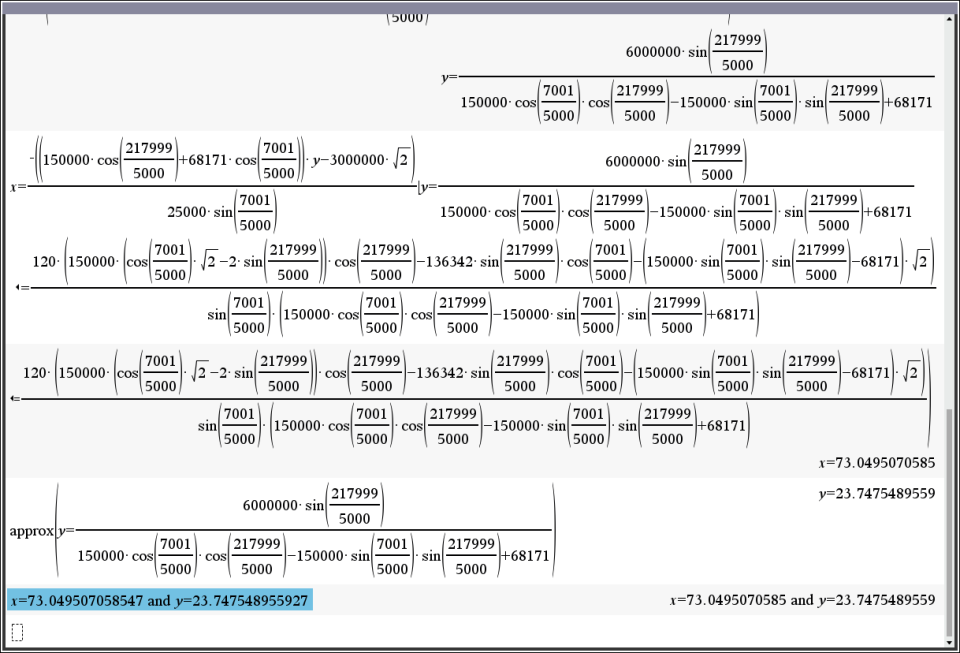
x=73.049507058547 and y=23.747548955927

어떤 solve로 나온 근사값이든, 근사값으로는 원래의 식 모두를 만족시킬 수 없음.
-
-
세상의모든계산기
그래프로 확인

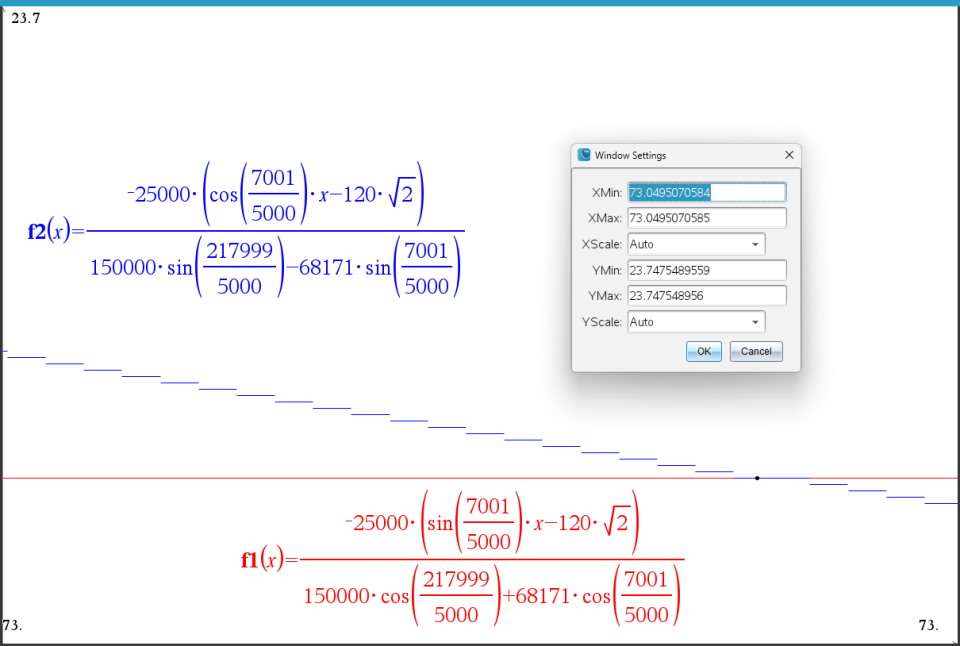
매우 좁은 구간으로 그래프를 확대해 보면
불연속적인 모습이 확인됩니다.
이것은 한계 digits(15자리) 이상을 처리하지 못하기 때문입니다.


