- TI 89
[TI-92][TI-89] Fourier Transform Library
-
- 2024.11.19 - 00:34 2024.11.15 - 23:18 3395 8
오리지널 출처는 모르겠구요. 이곳에서 발견했습니다.
https://helpcalculator.forumfree.it/?t=7760484
파일 다운로드 : https://digilander.libero.it/fpirozzi/fourier.zip
Readme.txt
fourier
-------
Fourier version 3.20 for TI-92/TI-92II and TI-89/TI-92+
This packet contains functions to perform Fourier-/inverse Fourier-
transformation. A function, which can rewrite the output of Fourier/
iFourie to a form that, can be evaluated numerical. A function to
graph the output.
Keep the functions together in a separate folder with the name
"FOURIER" and do not create any variable in it.
Before using iFourier or Fourier set TI-92 MODE
Complex Format to RECTANGULAR
Angle to RADIAN
Exact/Approx to AUTO
You have to do these settings yourself because; the functions cannot
change the mode setting on the calculator.
The package include following programs/functions:
Help online help to programs.
Fourier Fourier transformation
iFourier inverse Fourier transformation
Plot graph expression
eval evaluate expression
Menu custom menu
Other files in the package are all sub functions or data for above functions.
--------------------- Archiving on TI-89 and TI-92+ -------------------------
All variables can be archived on the TI-89 and TI-92+. Functions and programs can also be archived, but first after they have been used one time each. If
the programs have not been run before archiving, the calculator has to
compile them each time they are used, this will slow down the execution time
of the programs.
Before archiving the programs execute following commands from the command
line in the "fourier" folder:
Help() and press 'x'
ifourier(1/w,w)
fourier(1,t)
eval(1)
plot(1,t,0)
---------------------------------------------------------------------
Help
This program will give online information about and demonstrate the
use of functions in this package. When you do not need this program
any longer just delete it and the data file "hlp".
Syntax: Help()
---------------------------------------------------------------------
Function: Fourier(f(var), var ,mode)
Transforms the expression "f(var)" from time domain to frequency domain (Fourier). This function has the ability in the most occasions to perform symbolical transformations, but not in all. It depends on the type of transform.
f(var): can be any expression, which have a Fourier transform.
var : is the name of the variable to transform normally 't', but can be any name.
mode : decide the format of the result.
Mode can be 1 or 2.
In mode 1 the result will be in Ti-92's complex format (exp(i*w) will be rewritten to cos(w)+i*sin(w)). Mode 2 is a special format, where the calculators complex 'i' will be replaced with the letter 'i'.
The results in mode 2 will be exponential functions instead of sine and cosine. The letter 'i' in the results of Fourier is the same as the complex 'i' and can always be replaced with it.
The letter 'i' and 'complex i' will be interpreted as equal.
The expression may contain constants of any kind except constants
containing the letter 's'.
Special transforms:
Unit step function (Heaviside function):
Definition: u(t-a) = 1 for t>=a else 0
Fourier(u(t - a),t,2) = pi*'Delta'(w)-i*exp(-a*i*w)/w
Dirac delta function:
Definition: 'delta'(t - a) = 1 for t=a else 0
fourier('delta'(t - a),t,2) = exp(-a*i*w)
You can get 'delta' by pressing 'green diamond' + G + D on TI-92.
signum function:
Definition: signum(t-a) = 1 for t>=a else -1
Fourier(signum(t - a),t,2) = -i*2*exp(-a*i*w)/w
Some examples:
Fourier(cos(5*t),t,1) = pi*'delta'(w-5)+pi*'delta'(w+5)
Fourier(cos(5*t)*u(t),t,1) =
i*(-1/2*(w+5))-1/(2*(w-5))+pi*'delta'(w-5)+pi*'delta'(w+5)
Fourier(1/(t-i),t,2) = 2*pi*i*exp(w)*u(-w)
---------------------------------------------------------------------
Function: iFourier(F(var), var ,mode)
Transforms the expression "F(var)" from frequency domain to time domain
(inverse Fourier).
F(var): can be any expression, which have an inverse Fourier transform.
var : is the name of the variable to transform normally 'w', but can
be any name. This function has the ability in the most occasions to
perform symbolical transformations, but not in all. It depends on the
type of transform.
mode : decide the format of the result. Mode can be 1 or 2. In mode 1
the result will be in Ti-92's complex format (exp(i*w) will be rewritten
to cos(w)+i*sin(w)). Mode 2 is a special format, where the calculators
complex 'i' will be replaced with the letter 'i'. The results in mode 2
will be exponential functions instead of sine and cosine. The letter 'i'
in the results of iFourier is the same as the complex 'i' and can always
be replaced with it.
The letter 'i' and 'complex i' will be interpreted as equal.
The expression may contain constants of any kind except constants containing the letter 's'.
Special transforms:
Unit step function (Heaviside function):
Definition: u(w-a) = 1 for w>=a else 0
iFourier(u(w - a),w,2) = 'Delta'(-t)/2+i*exp(a*i*t)/(2*pi*t)
Dirac delta function:
Definition: 'delta'(w - a) = 1 for w=a else 0
Fourier('delta'(w - a),w,2) = exp(a*i*t)/(2*pi)
You can get 'delta' by pressing 'green diamond' + G + D on TI-92.
signum function:
Definition: signum(w - a) = 1 for w>=a else -1
Fourier(signum(w - a),w,2) = i*exp(a*i*t)/(pi*t)
Some examples:
iFourier(u(w+1)-u(w-1),w,1) = sin(t)/(pi*t)
iFourier(1/(w+1)^2,w,2) = 2*t*exp(-i*t)*(2*u(-t)-1)
iFourier('delta'(w+5)+'delta'(w-5),t,1) = sin(5*t)/pi
---------------------------------------------------------------------
Function: eval(f(var))
f(var) any function containing Heaviside, dirac delta or signum
This function will replace u(var), 'delta'(var), signum(var) with a
equivalent when-functions. The letter 'i' will be replaced with the
'complex i'.
Example: eval(u(t-a))=when(t-a>=0, 1,0)
To get a numerical result out of a function containing special
functions
eval(f(var))|var=value
---------------------------------------------------------------------
Program: Plot(f(var),var,type)
This program will graph functions containing Heaviside, dirac delta or
signum. It will not change the setting of the calculator and it is
therefore up to you to manage the window settings.
f(var) any function containing Heaviside, dirac delta or signum
var variable to plot
type=0 plot the function f(var)
type=1 plot the amplitude abs(f(var))
type=2 plot phase angle(f(var))
Example:
Plot(u(t)-u(t-4),t,0) plots a pulse
Example:
Plot the amplitude of a complex function
plot(f(war),var,1)
Plot the phase
plot(f(war),war,2)
---------------------------------------------------------------------
Author: Lars Frederiksen
E-mail: LTF@POST8.TELE.DK
PS. Please do not ask for more programs.
-
25
댓글8
-
-
세상의모든계산기
주요 함수들과 그들의 역할
1. fourier(α,β,β1) - 메인 함수
- 모드 체크를 수행합니다 (Exact/Approx, Complex Format, Angle)
- β1 값에 따라 다른 변환 방식을 선택합니다:
- β1=1 or 2: 일반적인 푸리에 변환
- β1=3 or 4: 주파수 도메인(2πf) 변환2. fourisub(α, ββ, β1, β2, β3, βi) - 실제 변환 연산
- 복소수 형태의 푸리에 변환을 계산합니다
- 주요 처리 과정:
- 입력 함수를 파싱하여 항들을 분리
- 각 항에 대해 적분 계산
- 델타 함수(δ), 단위계단 함수(u), 부호 함수(signum) 등의 특수 함수 처리3. eval(x) - 수식 평가 함수
- 특수 함수들을 계산 가능한 형태로 변환:
- u(x) → when(x>=0,1,0)
- δ(x) → when(x=0,1,0)
- signum(x) → when(x>=0,1,-1) -
세상의모든계산기
예시) x(t) = e^(-at)u(t) 처리 과정
1. 함수 입력 형태와 초기 처리:
# 입력 함수 형태
α = "e^(-a*s)*u(s)" # 여기서 s는 시간 변수# eval 함수에서 단위계단 함수 변환
# "u(s)" → "when(s>=0,1,0)"
inString(α, "u(")→αa # u( 위치 찾기
read(α, αa+1,")*+-/")→αb # 인자 추출 (여기서는 's')
# 변환 결과: "e^(-a*s)*when(s>=0,1,0)"2. fourier 함수에서의 처리:
fourier(α,β,β1)
# β는 변환 파라미터
# β1은 변환 타입 (1 또는 2: 기본 푸리에 변환)# fourisub 호출
fourier\fourisub(α, β, w, w, 0, @i)→α
3. fourisub 함수에서의 주요 변환 과정:
# 1) 입력 함수 파싱
expr(αa)→αk # 수식을 파싱하여 계산 가능한 형태로 변환
getDenom(αk)→βλ # 분모 추출
getNum(αk)→βf # 분자 추출# 2) 지수함수 처리
# e^(-a*s) 부분 처리
inString(αa,"@e^",αj)→αj # 지수함수 위치 찾기
read(αa, αj,"÷−)*/")→αi # 지수 부분 추출# 3) 기본 변환쌍에 대입해 변환
# timeδ 함수와 time 함수가 실제 변환을 처리합니다
timeδ(βρ,β1,β2,β4)→αf # βρ에는 변환할 항의 정보가 담겨있습니다
# 변환 결과들은 누적됩니다
βa+αf/βλ→βa # 부분 결과들의 합산
# 특별한 경우(poles가 있는 경우) 처리
If dim(βγ)>0 Then
# βγ는 극점들의 배열
# 각 극점에 대해 처리하는 루프
For βς,1,dim(βγ)-1
Φα*(s-#("Γ"&char(ord("a")+βς)))→Φα
EndFor
# 4) 결과 조합
β3*(βa+Φw)|i^2=-1→Φw # 최종 결과 생성
수학적 계산 흐름:
1. x(t) = e^(-at)u(t)가 입력됨
2. u(t)가 when(t>=0,1,0)로 변환됨
3. 푸리에 변환 적분 적용:
X(ω) = ∫[e^(-at)u(t)e^(-jωt)]dt
4. u(t)의 특성으로 인해 적분 구간이 0에서 ∞로 변경됨
5. 적분 계산:
X(ω) = ∫[e^((-a-jω)t)]dt, from 0 to ∞
6. 적분 결과:
X(ω) = 1/(a + jω)이 과정이 코드에서 자동으로 처리되며, 특히 주목할 점은:
- 특수함수(여기서는 u(t))의 자동 변환
- 복소수 처리 (i^2=-1 조건 사용)
- 지수함수의 적분 처리
- 최종 결과의 표준화된 형태 제공이는 단순한 예시지만, 코드는 더 복잡한 함수들(예: 델타 함수, 부호 함수 등을 포함하는 함수들)도 처리할 수 있도록 설계되어 있습니다.
-
-
세상의모든계산기
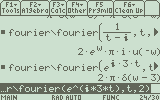
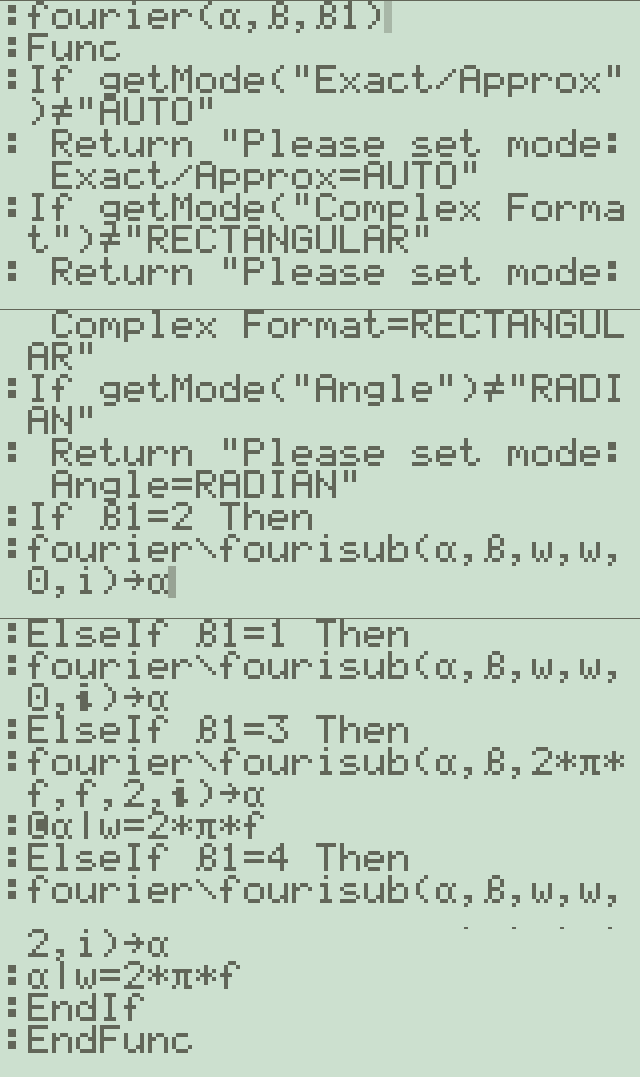
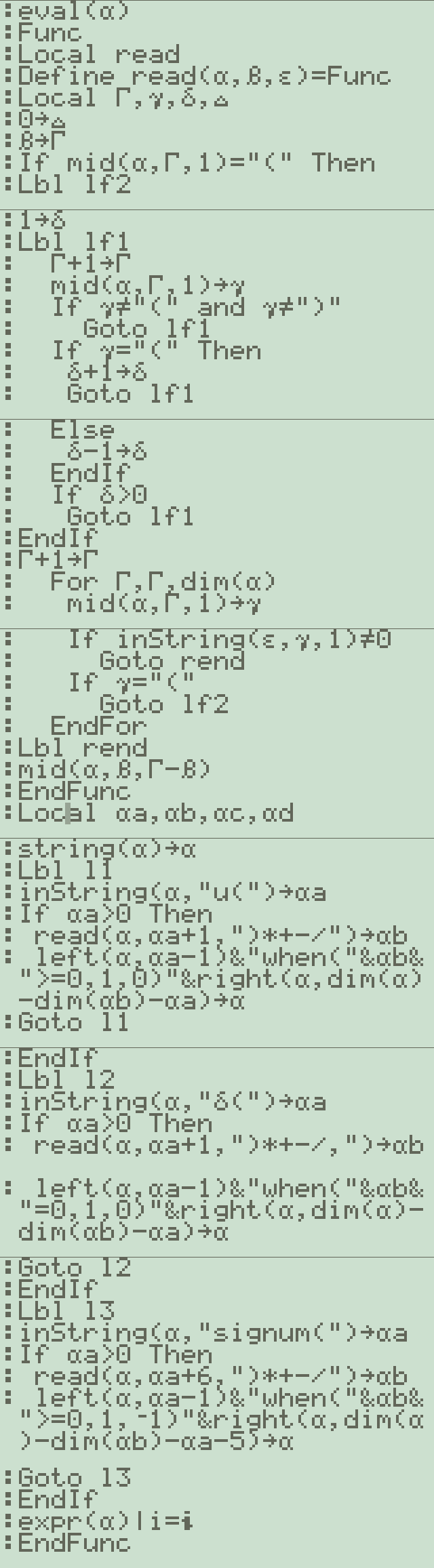
function - fouriersub()
클릭해 프로그램(png) 보기 - 스크롤 주의
details
-
세상의모든계산기 님의 최근 댓글
- claude AI는 l-c*r^2 을 1-c*r^2 으로 잘못 읽고 표시하고 있습니다. - TI-nspire CAS 계산기에 l-c*r^2 ≥0 을 조건에 추가해 계산해 보아도 결과는 바뀌지 않습니다. 2026 07.20 ⚠️ 경고가 바로 두 번째 방법이 "성공"한 이유와 정확히 연결되어 있습니다. 경고의 의미 "Domain of the result might be larger than the domain of the input"는 CAS가 절댓값(모듈러스)을 계산하는 과정에서 원래 식보다 정의역이 더 넓은 형태로 단순화했다는 뜻입니다. 구체적으로 이 계산은 내부적으로 대략 이런 과정을 거칩니다. $$\left|\frac{er}{e\cdot r}\right| = \sqrt{\left(\frac{er}{e\cdot r}\right)\cdot\overline{\left(\frac{er}{e\cdot r}\right)}}$$ 즉 원래 식(복소수)과 그 켤레복소수를 곱해서 실수부·허수부 제곱합을 만들고, 거기에 다시 제곱근을 씌우는 과정입니다. 이 과정에서 √(x²) → x 또는 √a·√b → √(ab) 같은 규칙들이 쓰이는데, 이런 규칙들은 x가 실수이고 0 이상일 때만 엄밀하게 성립합니다. CAS는 이 조건들을 일일이 다 추적하지 않고 넘어가면서, 원래는 (e≠0, r+l·ω·i ≠ 0 등) 복소수 특유의 좁은 정의역을 가진 식을, r, l, ω가 어떤 실수여도(부호 무관하게) 정의되는 1/√(r²+l²·ω²)라는 더 넓은 정의역의 식으로 바꿔버린 것입니다. CAS는 이 손실을 감지하고 경고를 띄운 것입니다. 이게 왜 조건 대입 성공과 연결되는가 정리하면, 이 경고는 사실상 이런 뜻입니다. "나는 이 결과를 만들면서 원래 식이 가지고 있던 정의역 제약 정보(부호 조건, i 관련 조건 등)를 이미 버렸다." 바로 이 "정의역 정보를 버린" 상태가 이후 con_1 대입을 매끄럽게 만드는 원인입니다. 첫 번째 시도에서는 i가 살아있는 원래 식에 조건을 대입했기 때문에, CAS가 √(1-c·r²)이 실수인지(정의역 조건: 1-c·r² ≥ 0) 계속 추적하려고 했고, 그 정보가 con에 없어서 더 이상 정리를 못 하고 멈췄습니다. 두 번째 시도에서는 절댓값 계산 단계에서 이미 그런 세밀한 정의역 추적을 CAS 스스로 포기(단순화)했기 때문에, 이후 ω에 무리식을 대입해도 "이게 실수가 맞나?" 하는 검증 절차 없이 그냥 대수적으로 치환·정리해 버립니다. 그래서 깔끔하게 √c/√l이 나온 겁니다. 한 줄 요약 절댓값 계산 시 뜬 "정의역이 넓어졌을 수 있다"는 경고는, CAS가 그 순간에 원래 식의 엄밀한 조건(정의역)을 놓쳤다는 신호이고, 바로 그 "조건을 놓친 상태"이기 때문에 뒤에 이어지는 조건식 대입이 막힘없이 진행된 것입니다. 다만 그 대가로, 결과인 1/√(r²+l²·ω²)이나 최종 √c/√l이 원래 회로 조건(i≠0이 되는 경계, 분모가 0이 되는 경우 등)에서는 엄밀히 성립하지 않을 수 있다는 점은 감안하셔야 합니다. 실제 물리적으로는 r, l, c > 0이고 결과도 물리적으로 타당한 형태라 문제없어 보이지만, 수학적 엄밀성 측면에서는 "정의역이 넓어진 근사적 결과"라는 꼬리표가 붙어있는 셈입니다. 2026 07.20 Claude AI 답변 TI-Nspire CAS의 | (such that / 조건대입) 연산자는 대입 시점의 수식 형태를 그대로 두고 기호만 치환하는 연산입니다. 대입 후에 처음부터 다시 "실수부/허수부 분리, 유리화" 같은 재간소화를 자동으로 수행하지 않습니다. 이 차이가 지금 보신 결과 차이의 핵심입니다. 첫 번째 경우 (|er/(e·r)| | con_1 and con → 실패) 이 시점의 식은 아직 r + l·ω·i 형태의 복소수 그대로입니다 (i가 살아있음). 여기에 con_1: ω = √(1-c·r²)/(√c·l)을 대입하면, 분모 안에 i · √(1-c·r²) 라는 항이 새로 생깁니다. 문제는 CAS가 √(1-c·r²)이 실수인지(즉 1-c·r² ≥ 0인지) 판단할 근거가 없다는 겁니다. 저장해 두신 con 조건은 c>0, l>0, r>0뿐이고, 1-c·r²≥0이라는 조건은 포함되어 있지 않습니다. 그래서 CAS는 i와 이 무리식을 더 정리(유리화, 실수부·허수부 재결합)하지 못하고 있는 그대로 남겨둡니다. 결과에 여전히 i가 보이는 이유입니다. 두 번째 경우 (결과값 1/√(r²+l²·ω²)에 대입 → 성공) |er/(e·r)| (절댓값/모듈러스) 연산은 그 자체로 이미 "복소수 → 실수" 변환을 완료한 결과입니다. 즉 1/√(r²+l²·ω²)에는 더 이상 i가 없고, 순수하게 r, l, ω로만 이루어진 실수식입니다. 이 식에 ω = con_1을 대입하는 것은 그냥 실수 대수식에 실수 대입하는 것이므로, i와 무리식이 뒤엉키는 문제 자체가 발생하지 않습니다. 그래서 바로 깔끔하게 √c/√l로 정리됩니다. 정리하면 절댓값(모듈러스) 계산은 "이 값들이 실수다"라는 가정을 이미 내부적으로 써서 i를 제거하는 연산입니다. 그 연산을 조건 대입 이전에 해두면, 이후 대입은 단순 실수 대입이라 문제없이 정리됩니다. 반대로 i가 남아있는 식에 무리식을 포함한 조건을 먼저 대입하면, 그 무리식의 실수성/부호에 대한 가정이 없어서 CAS가 i를 소거하는 재간소화를 못 하고 멈춰버립니다. 실용적 팁: 복소식에 조건을 대입해야 할 때는 가능하면 절댓값·실수화(유리화) 등을 먼저 끝내서 i를 없앤 뒤 조건을 대입하거나, 대입 후 결과에 다시 simplify/expand/combine 같은 명령을 한 번 더 걸어주면 (필요한 도메인 조건과 함께) 정리가 되는 경우가 많습니다. 2026 07.19 저도 어림잡아 추측할 뿐이지 정확한 이유를 알지는 못합니다. 질문하신 사진을 그대로 (Gemini 3.5 Flash / ChatGPT / Claude Sonnet 5) AI에 넣어 보니 claude AI 가 제일 합리적인 답변을 주어서 이를 붙여 넣습니다. 2026 07.19 아 그렇네요. 감사합니다. ^^ 2026 04.28