- TI nspire
[TI-nspire] 그래프 - 미분 방정식 Diff Eq
-
- 2024.07.18 - 14:53 2019.02.06 - 12:35 2488 4
1. 그래프 모드 - 미분 방정식 Diff Eq
- 미분 방정식 그래프 모드에서는 (대수적으로 시스템을 특징짓는) 미분 방정식을 풀지 않고도, 역동적인 과정(변화)를 탐색할 수 있습니다.
- 새로운(OS Ver 3.0에서 업데이트됨) 2D 그래프 유형인 미분 방정식은 미분 방정식의 해를 근사화하는 슬로프(Slope) 필드와 방향(Direction) 필드의 플롯을 제공합니다. 사용자는 Euler와 Runge-Kutta 해법 중에서 선택할 수 있습니다.
- (여러) 초기 조건에 따라 특정 솔루션을 시각화 할 수 있습니다. 초기 조건은 좌표 평면에서 드래그 할 수 있으며 특정 솔루션이 자동으로 업데이트됩니다.
- 그래프 유형 미분 방정식은 동일한 좌표계에서 다른 2D 그래프 유형과 결합 될 수 있습니다.
(TI-nspire OS Ver3 Release Note 에서 발췌)
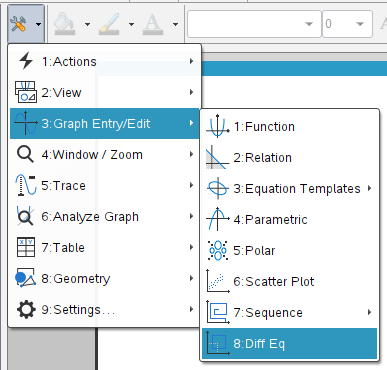
2. 옵션
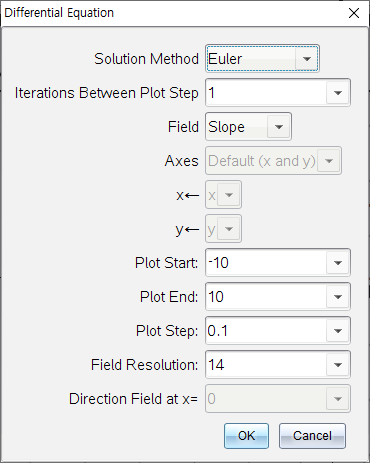
- Solution Method(수치해석 방법) :
Euler / Runge-Kutta 중 선택
- Iterations between plot step(Euler 방법에서 계산의 정확도 결정) : 1 ~ 정수값
Error Tolerance(RK방법에서 오차 허용) : 허용 범위 ≥ 1x10^-14
- Field(장) :
None - 표시하지 않음
Slope - 경사
Direction - 두 미분 방정식 사이의 관계를 나타내는 기울기 방향
- Axes :
Default(x and y)
Custom - 2개이상 미분 방정식일 때 사용
The available entries are :- x 독립변수
- y1 and y2 (or any other identifiers defined in the editor)
- y1’ and y2’ (or any other derivatives defined in the editor)
- Plot Start :
솔루션 플롯이 시작되는 독립 변수값을 결정 - Plot End :
솔루션 플롯이 끝나는 독립 변수값을 결정 - Plot Step :
값이 표시될 독립변수 값의 증가량을 결정
- Field Resolution :
Field 표시할 열의 갯수 결정
- Direction Field at x= :
방향 필드가 그려지는 독립변수의 값을 설정
3. 예시 y'=2x, y(0)=1
1. y'=2x, y(0)=1 인 미분 방정식을 이용해 그래프를 그려 보겠습니다.
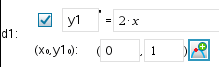
x는 그냥 x로,
y는 y1 또는 y2로 입력합니다. (좌변, 우변 모두에서)
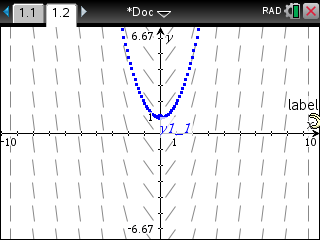
2. 미분 방정식을 풀면 y=x^2 + 1 이 됩니다.
이 그래프를 겹쳐 확인해 보면 얼추 같아 보입니다.
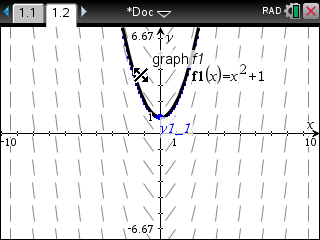
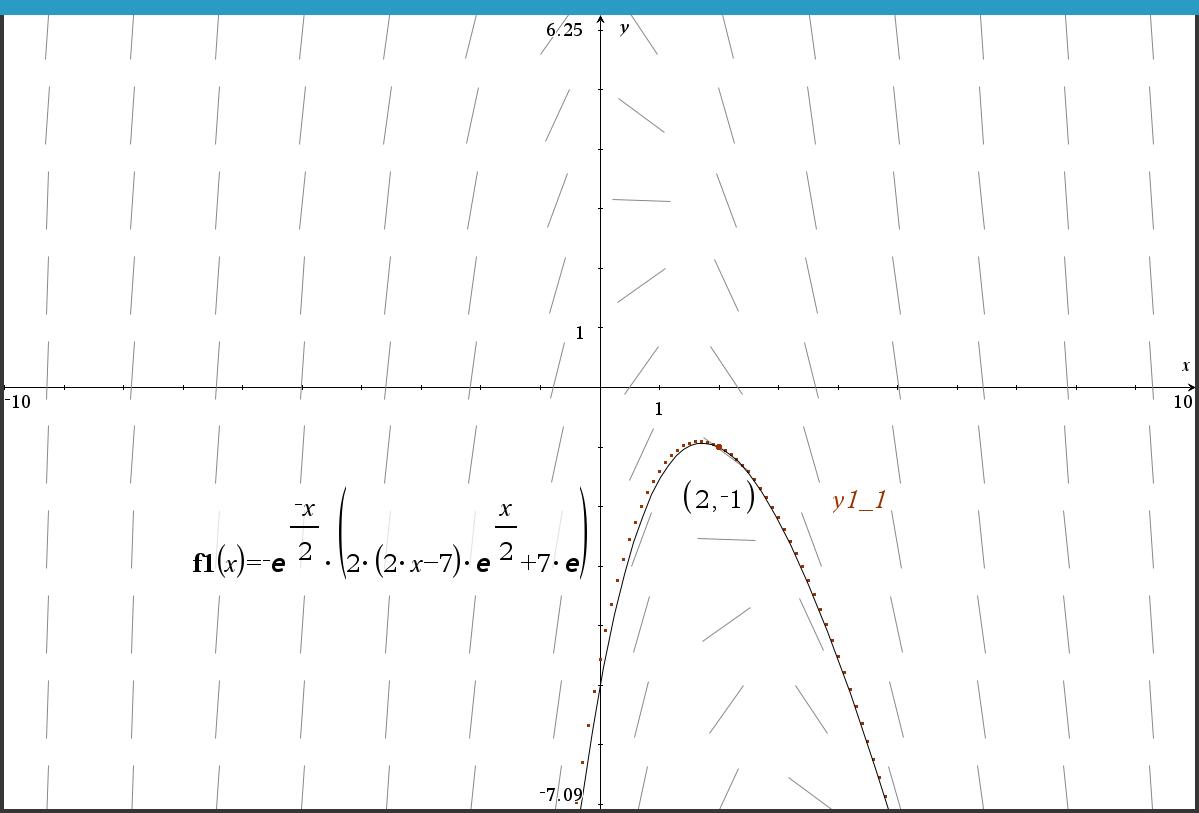
3. 하지만 확대해 보면... 원래 그래프와는 오차가 있습니다.
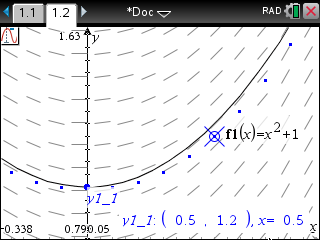
f1(0.5) = 0.5^2+1 = 1.25
4. 이를 해결하기 위해 Diff Eq 엔트리 옵션에서 Iterations Between Plot Step 을 기본값인 1에서 10으로 올려 보았습니다.
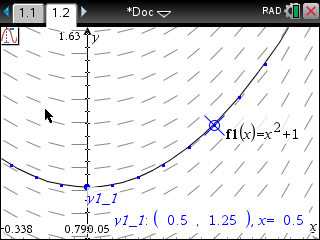
오차가 줄어들었습니다. 그래도 점 찍힌 모양새가 원 그래프와 일치하지는 않는 것 같습니다.
Iteration 횟수를 늘리는 대신 Plot Step 을 줄여도 오차는 줄어듭니다.
5. Plot Step 을 줄이면 점 찍히는 간격이 줄어 촘촘해지는 것은 확실한데,
Plot Start / End 는 정확히 어떤 역할을 하는지 잘 모르겠습니다.
6. 초기 조건이 여럿인 경우 그래프도 여럿이 출력됩니다.
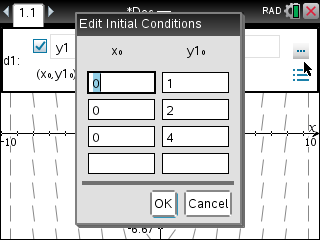
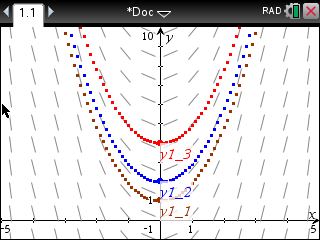
4. 주의
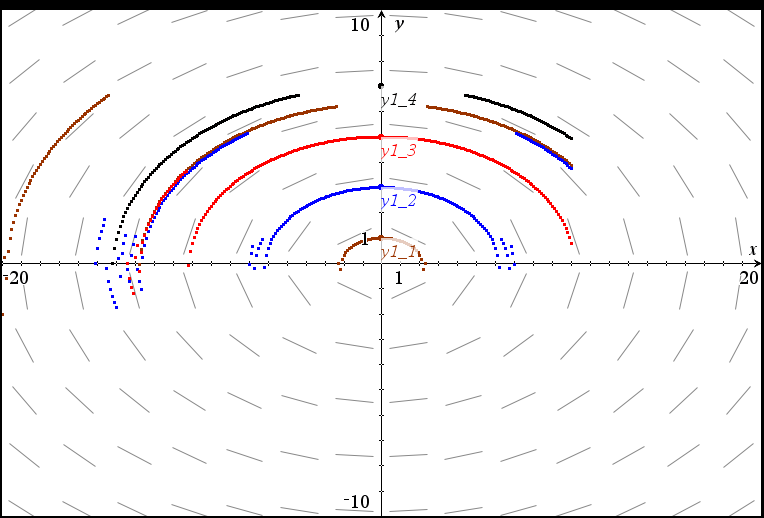
초기 조건값의 선택에 따라 plot 그려지는게 달라질 수 있습니다. 초기 조건값을 만족하는 그래프plot이 딱 하나일 수도 있지만, 여러개일 가능성도 있기 때문입니다.
초기 조건값을 여러개 넣는 경우, (desolve 함수와 달리) 모든 조건값을 동시에 만족하는 그래프를 찾는 것이 아니고, 각각의 조건값을 만족하는 모든 그래프를 모조리 찾기 때문에, 조건값은 가급적 하나만 넣는 것이 바람직한 것 같습니다.
그리고 slope(기울기)가 0 또는 ∞ 이 되는 점을 초기값으로 주는 것은 바람직하지 않은 것 같기도 한데, 이것 역시 케이스바이케이스입니다.
-
25
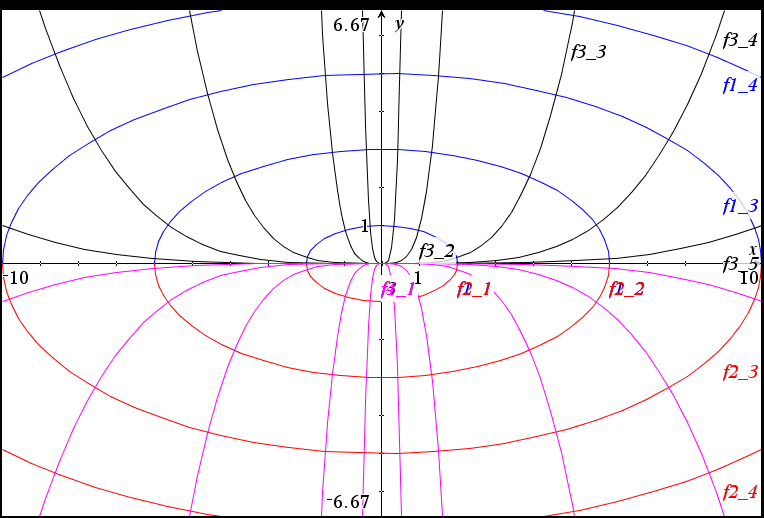
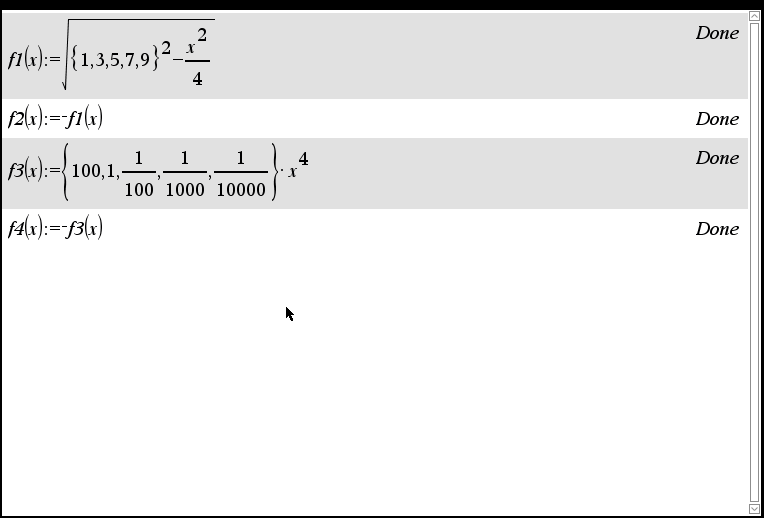
세상의모든계산기 님의 최근 댓글
HP-39gII 에 ExistOS 설치하기 https://allcalc.org/38526 2025 11.07 1. 왜 검은색이 아닌 다른 색으로 보일까? (제공된 LUT 필터) 제가 제공해 드린 magenta_lens.cube LUT 필터는 540~560nm(녹색-노란색) 파장대의 색상을 '완전히 제거(검은색으로 만듦)'하는 대신, '다른 색상으로 왜곡/변환'하도록 설계되었습니다. * 원리: LUT(Look-Up Table)는 특정 입력 색상(Input RGB)을 미리 정해진 다른 출력 색상(Output RGB)으로 매핑하는 테이블입니다. 이 LUT는 540~560nm에 해당하는 RGB 값들이 들어오면, 검은색(0, 0, 0)이 아닌, 매우 어둡거나 채도가 낮은 특정 색(예: 어두운 올리브색, 갈색 등)으로 변환하라고 지시합니다. * 의도: * 현실적인 물리 필터 시뮬레이션: 실제 고가의 색약 보정 안경도 특정 파장을 100% 완벽하게 차단하지는 못합니다. 빛의 일부를 흡수하고 일부는 통과시키거나 변환하는데, 이 LUT는 그러한 현실 세계의 필터 효과를 더 비슷하게 흉내 냈을 수 있습니다. * 시각적 정보 유지: 특정 색을 완전히 검게 만들면 그 부분의 형태나 질감 정보가 완전히 사라집니다. 하지만 다른 어두운 색으로 대체하면, 색상 정보는 왜곡되더라도 밝기나 형태 정보는 어느 정도 유지되어 전체적인 이미지가 덜 어색하게 보일 수 있습니다. 결론적으로, 스펙트럼 그림에서 해당 대역의 색이 갑자기 '다른 색으로 툭 바뀌는' 현상은, LUT 필터가 "이 파장대의 색은 앞으로 이 색으로 표시해!"라고 강제적으로 지시한 결과이며, 이것이 바로 이 필터가 작동하는 방식 그 자체입니다. 2. 왜 'Color Vision Helper' 앱은 검은색으로 보일까? 비교하신 'Color Vision Helper' 앱은 노치 필터의 원리를 더 이상적(Ideal)이고 교과서적으로 구현했을 가능성이 높습니다. * 원리: "L-콘과 M-콘의 신호가 겹치는 540~560nm 파장의 빛은 '완전히 차단'되어야 한다"는 개념에 매우 충실한 방식입니다. * 구현: 따라서 해당 파장에 해당하는 색상 정보가 들어오면, 어떠한 타협도 없이 그냥 '검은색(RGB 0, 0, 0)'으로 처리해 버립니다. 이는 "이 파장의 빛은 존재하지 않는 것으로 처리하겠다"는 가장 강력하고 직접적인 표현입니다. 2025 11.06 적용사례 4 - 파장 스펙트럼 https://news.samsungdisplay.com/26683 ㄴ (좌) 연속되는 그라데이션 ➡️ (우) 540 이하 | 구분되는 층(색) | 560 이상 - 겹치는 부분, 즉 540~560 nm 에서 색상이 차단? 변형? 된 것을 확인할 수 있음. 그럼 폰에서 Color Vision Helper 앱으로 보면? ㄴ 540~560 nm 대역이 검은 띠로 표시됨. 완전 차단됨을 의미 2025 11.05 빨간 셀로판지로도 이시하라 테스트 같은 숫자 구분에서는 유사한 효과를 낼 수 있다고 합니다. 색상이 다양하다면 빨강이나, 노랑, 주황 등도 테스트해보면 재밌겠네요. 2025 11.05 안드로이드 앱 - "Color Vision Helper" 다운받아 본문 내용을 카메라로 찍어 보니, 본문 프로그램에서는 애매하게 보이던 부분에서도 구분이 완전 확실하게 되네요. 숫자 구분 능력 & 편의성 면에서 압도적이라고 할 수 있겠습니다. 2025 11.05