[공학용 계산기] 지수(^)와 루트(√)의 입력, exponent and root
-
- 2024.11.14 - 15:53 2016.01.15 - 00:16 127227 7
1. 계산기에서 지수와 루트의 입력
* 지수(=n승) 입력
계산기에는 지수입력 버튼이 있습니다. 하지만, 계산기마다 지수관련 버튼의 수가 다를 수 있습니다.
- 【x²】 : 제곱 버튼, 가장 많이 사용되는 지수버튼으로 (아마도) 모든 공학용계산기에 있습니다.
- 【x³】 : 세제곱 버튼, 저가형 계산기에는 따로 있을 가능성이 높습니다.
세제곱 버튼이 없는 경우에는, '키 조합 방식' 【SHIFT】【x²】으로 입력 가능할 수도 있습니다.
버튼이 없다면, 아래처럼 n제곱 버튼을 사용해야 합니다.
- 【^】 : n제곱 버튼입니다. 계산기마다 표시가 다를 수 있습니다.
카시오 [fx-570ES]에서는 【x■】 버튼입니다.
샤프 [EL-509W]에서는 【yx】 버튼입니다.
* n루트(=n제곱근) 입력
- 【√】 : 제곱근 버튼, 많이 사용기 때문에 별도로 배정되어 있습니다.
루트 앞머리에는 2가 생략되어 있다고 생각하시면 됩니다.
만약 별도 배정되어 있지 않다면 '제곱 버튼'의 '키 조합 방식'으로 입력될 가능성이 높습니다.
- 【³√】 : 세제곱근 버튼, 자주 사용되지 않기 때문에 별도로 존재하지 않는 것이 일반적입니다.
이 때, 세제곱 키【x³】가 따로 있다면, 역시 '키 조합 방식'으로 세제곱근이 배정될 가능성이 높습니다.
세제곱 키가 따로 없으면, 세제곱근 키 조합도 따로 없습니다.
이 때도 역시나 n제곱근 키를 이용합니다.
- 【ⁿ√】 : n제곱근 버튼, 역시 따로 존재하지 않는 것이 보통입니다.
계산기에 따라 【x√】 로 표기되기도 합니다.
n제곱 버튼(【^】 또는 【x□】 또는 【yx】)의 '키 조합 방식'으로 입력됩니다.
예시 fx-350MS) 32의 5제곱근이라면 【5】【SHIFT】【^】【32】【=】순서로 누릅니다.
* 키 조합 방식 이란, 【SHIFT】 또는 【ALPHA】 또는 【2nd F】 와 같은 키를 먼저 누른 다음에 다른 키를 누르는 방식을 의미합니다.
컴퓨터 키보드에서 쌍자음 누르는 것과 유사하다고 생각하시면 됩니다.
동시에 누를 필요는 없고 순차적으로 누릅니다.
2. 지수(^)와 루트(√)의 관계
지수와 루트는... 모양새는 다르지만 (본질은) 서로 다르지 않습니다.
그래서 루트꼴 ⇔ 지수꼴 서로 바꾸어 계산할 수도 있습니다.
예)
계산기에서 지수, 루트를 조합방식으로 입력하기 귀찮은 경우나 루트가 꼴보기 싫은 경우에는,
n제곱 버튼【^】 하나로 n제곱과 n제곱근을 모조리 입력할 수도 있습니다.
3. 주의사항
괄호
지수와 제곱근 기호는 계산 우선순위가 사칙연산보다 높습니다.
그래서 한줄입력형 계산기에서는 지수부나 n제곱근의 내부가 단일숫자가 아니라면, 괄호로 꼭 묶어주어야 합니다.
한줄입력이 아닌 템플릿(네모칸) 입력형 계산기에서는 괄호가 꼭 필요하진 않습니다.
그래서 저는 모든 분들이 계산기 구매하실 때, 한줄입력 방식 계산기를 구매하지 않으셨으면 합니다.
달인 급으로 익숙해지는 경우에는 입력 속도가 오히려 더 빠를 수도 있지만, 그렇지 않다면 무조건 템플릿을 이용한 입체적 입력이 효율적입니다.
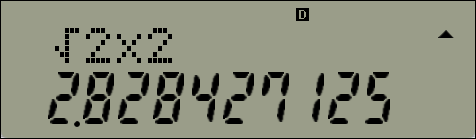
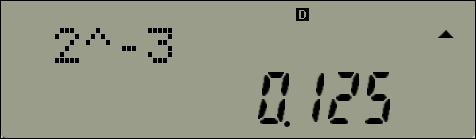
음수인 지수
음수 입력은 빼기버튼 【－】 말고 음수버튼 【(-)】 을 누르시는 것을 습관화하세요.
구분하지 않을 때 Syntax ERROR 가 나는 기종이 있고, 자동 변경을 지원해서 에러가 나지 않더라도 종종 입력 실수를 유발합니다.
참고 글 : [공학용 계산기] 빼기 기호 【－】 와 음수 기호 【(-)】 의 구분 https://allcalc.org/5876
e 자연상수의 입력
공학용 계산기에서는 자연상수 'e' 를 단독으로 쓸 일도 많고, e의 지수승인 'e^' 을 쓸 일도 많아서, 둘을 입력하는 버튼이 각각 존재하는 경우가 보통입니다.
(입체적 입력방식이 아닌) 1줄 입력방식일 때는 둘을 혼동할 수 있기 때문에 주의하여야 합니다. (잘 못 사용시 error 가 발생합니다)
※ 늘 하는 얘기지만... 계산기마다 다를 수 있습니다.
예) [fx-350MS]
e 단독: 【ALPHA】【ln】 으로 입력.
기울어진 e로 표현됩니다. (표현방식은 계산기마다 다를 수 있습니다)
(다른 문자변수와 같이) 지수 추가 입력시에는 【^】 기호를 삽입해야 합니다.
-----------------------------------------------------------------------------------------
e^ : 【SHIFT】【ln】 으로 입력. (화면상에는 ^가 생략되어 표시)
(e 단독)과 달리 기울어지지 않은 e 로 표현.
지수 입력시 【^】 기호 삽입하면 오히려 에러가 발생합니다.
지수를 생략하고 빈칸으로 두어도 에러가 발생합니다.
EXP 또는 EE
【EXP】 또는 【EE】 또는 【EEX】로 표시된 버튼이 있습니다. 수학에서는 exp(x) 함수가 e^x 함수로 사용되지만, 계산기에서는 보통 ×10^(x) 를 의미하는 E 입력버튼으로 사용됩니다. 굳이 이름붙이자면 "10의 지수?", "상용지수?함수"라고 할 수 있을까요?
아무것도 없다면 보통은 【×10^(x)】 버튼이 있습니다.
| 【×10^(x)】 | fx-570 시리즈 |
| 【EXP】 | fx-9860G 시리즈, EL-509W 등 |
| 【EE】 | TI-nSpire 시리즈 |
| 【EEX】 | HP PRIME, HP-50g, |
-
25
댓글7
-
자연상수의 복소수 지수가 들어가면 i에 곱해진 숫자가 극좌표의 각도를 의미하므로 극좌표 ∠를 이용하면 됩니다. 다만 e의 지수에 들어가는 숫자는 무조건 호도법의 각도이므로 각 입력 모드를 라디안으로 하셔야 합니다. e^12.7i이것을 예로 든다면 라디안 각으로 1∠12.7을 입력한 것과 같습니다.
-
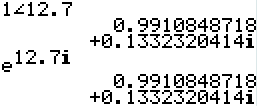
세상의모든계산기
1. EQN
제곱, 세제곱, 네제곱 같이 정형화된 수식은 Eqn 모드에서
해를 찾는 것이 가장 좋습니다.
https://allcalc.org/6063
2. Solve
Eqn 으로 구하지 못하는 수식은 Solve 를 이용하실 수 있습니다.
-
세상의모든계산기
3. EQN 이나 Solve 를 사용할 수 없는 fx-350ES 나 fx-350MS 와 같은 계산기에서
손으로 X = ~~~~~~ 꼴로 정리한 다음
정리된 부분만 계산기에 넣어 계산합니다.x^3 = 3.53*10^-23
x= (3.53*10^-23)^(1/3)
【(】【3.53】【×】【10】【^】【(-)】【23】【)】【^】【(】【1】【÷】【3】【)】【=】
※ 지수부 -23 을 입력할 때 빼기기호【-】 입력하지 마시고 음수부호【(-)】를 사용하세요.
-
세상의모든계산기
[UC-400M] exp*(-0.0075/1.5^2) 을 어떻게 입력하나요?
1. [UC-400M] 은 [fx-350MS] 의 설명글을 찾아보시면 됩니다.
2. 【SHIFT】【ln】【(】【(-)】【0.0075】【÷】【1.5】【x²】【)】【=】
또는
3. 【ALPHA】【ln】【(】【(-)】【0.0075】【÷】【1.5】【x²】【)】【=】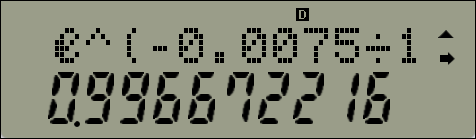
세상의모든계산기 님의 최근 댓글
엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10 [일반계산기] 매출액 / 원가 / 마진율(=이익율)의 계산. https://allcalc.org/20806 2026 02.08 V2 갱신 (nonK / K-Type 통합형) 예전에는 직접 코드작성 + AI 보조 하여 프로그램 만들었었는데, 갈수록 복잡해져서 손 놓고 있었습니다. 이번에 antigravity 설치하고, 테스트 겸 새로 V2를 올렸습니다. 직접 코드작성하는 일은 전혀 없었고, 바이브 코딩으로 전체 작성했습니다. "잘 했다 / 틀렸다 / 계산기와 다르다." "어떤 방향에서 코드 수정해 봐라." AI가 실물 계산기 각정 버튼의 작동 방식에 대한 정확한 이해는 없는 상태라서, V1을 바탕으로 여러차례 수정해야 했습니다만, 예전과 비교하면 일취월장 했고, 훨씬 쉬워졌습니다. 2026 02.04 A) 1*3*5*7*9 = 계산 945 B) √ 12번 누름 ㄴ 12회 해도 되고, 14회 해도 되는데, 횟수 기억해야 함. ㄴ 횟수가 너무 적으면 오차가 커짐 ㄴ 결과가 1에 매우 가까운 숫자라면 된 겁니다. 1.0016740522338 C) - 1 ÷ 5 + 1 = 1.0003348104468 D) × = 을 (n세트) 반복해 입력 ㄴ 여기서 n세트는, B에서 '루트버튼 누른 횟수' 3.9398949655688 빨간 부분 숫자에 오차 있음. (소숫점 둘째 자리 정도까지만 반올림 해서 답안 작성) 참 값 = 3.9362834270354... 2026 02.04