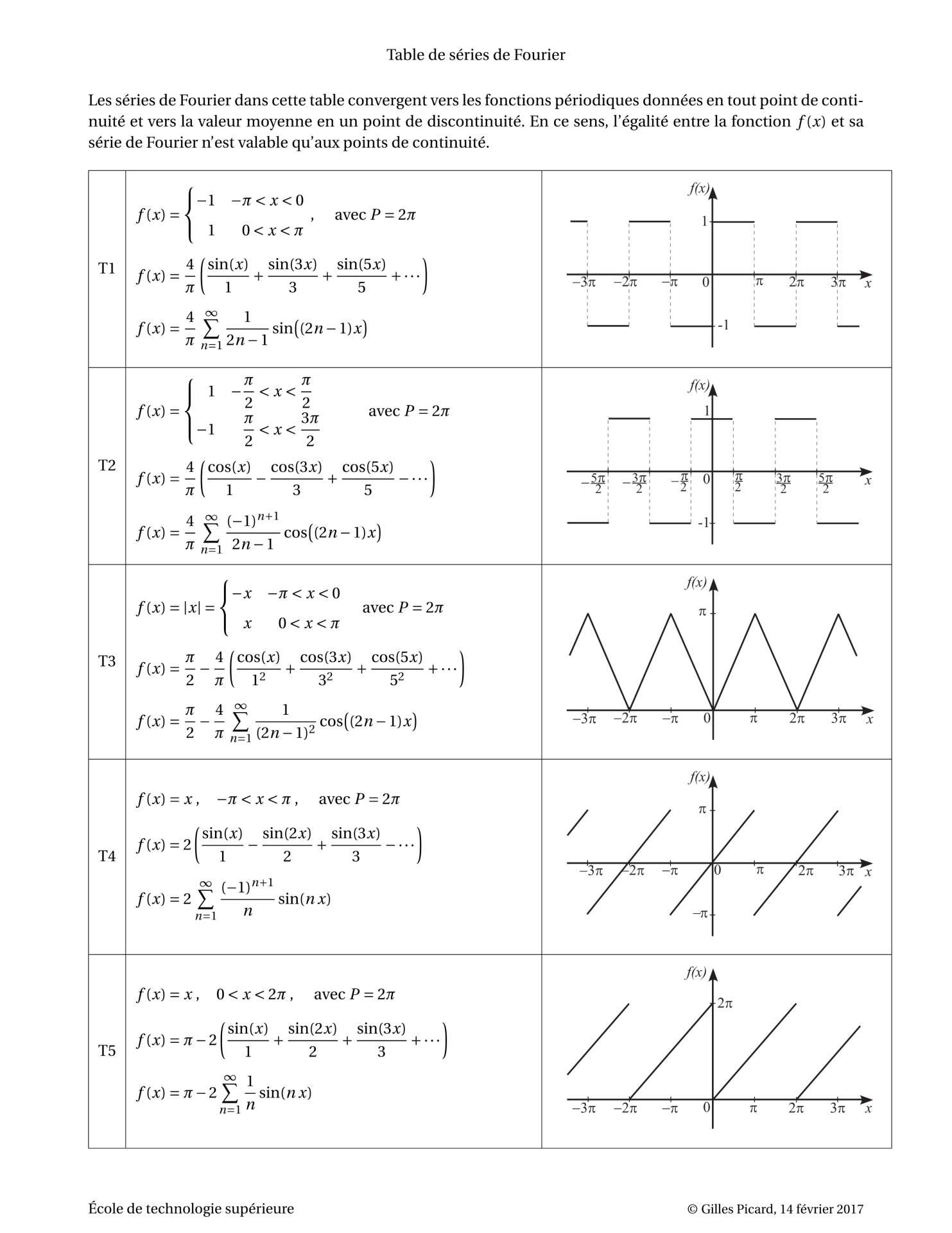
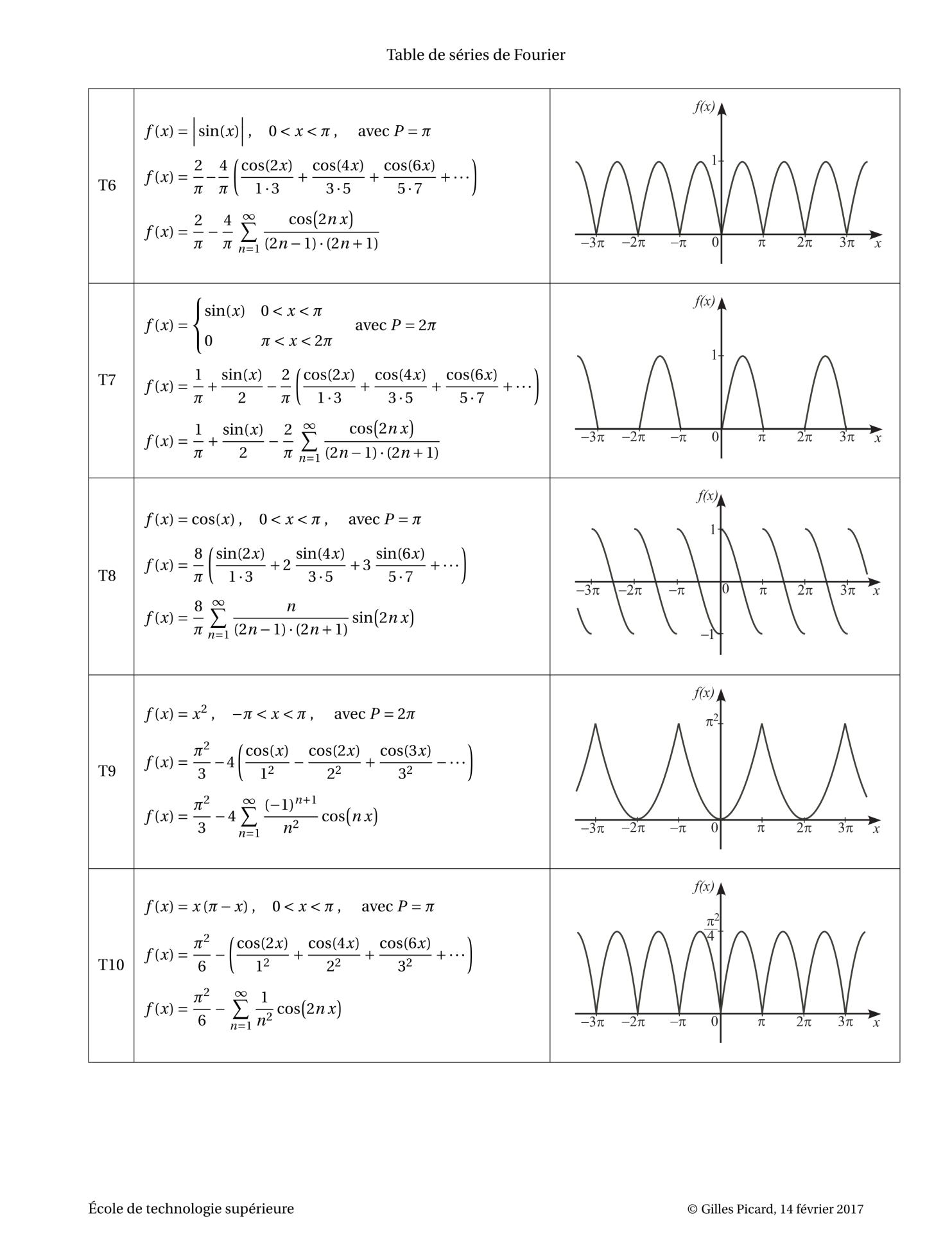
푸리에 급수 테이블 , 푸리에 변환 테이블, Fourier Series Table, Fourier Transform Table

세상의 모든 계산기 수학, 과학, 공학 이야기 ()

푸리에 급수 테이블 , 푸리에 변환 테이블, Fourier Series Table, Fourier Transform Table

- 세상의모든계산기
- 2024.11.15 - 00:05 2024.11.14 - 11:27 622

출처 : https://ena.etsmtl.ca/pluginfile.php/137982/mod_resource/content/8/Fourier-table.pdf

출처 : https://en.wikipedia.org/wiki/Fourier_transform

Functional relationships, one-dimensional

The Fourier transforms in this table may be found in [Erdélyi 1954] or [Kammler 2000, appendix].

	Function	Fourier transform unitary, ordinary frequency	Fourier transform unitary, angular frequency	Fourier transform non-unitary, angular frequency	Remarks
	\[f(x)\]	\[\begin{align} &\widehat{f}(\xi) \triangleq \widehat {f_1}(\xi) \\&= \int_{-\infty}^\infty f(x) e^{-i 2\pi \xi x}\, dx \end{align}\]	\[\begin{align} &\widehat{f}(\omega) \triangleq \widehat {f_2}(\omega) \\&= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align}\]	\[\begin{align} &\widehat{f}(\omega) \triangleq \widehat {f_3}(\omega) \\&= \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align}\]	Definitions
101	\[a\, f(x) + b\, g(x)\]	\[a\, \widehat{f}(\xi) + b\, \widehat{g}(\xi)\]	\[a\, \widehat{f}(\omega) + b\, \widehat{g}(\omega)\]	\[a\, \widehat{f}(\omega) + b\, \widehat{g}(\omega)\]	Linearity
102	\[f(x - a)\]	\[e^{-i 2\pi \xi a} \widehat{f}(\xi)\]	\[e^{- i a \omega} \widehat{f}(\omega)\]	\[e^{- i a \omega} \widehat{f}(\omega)\]	Shift in time domain
103	\[f(x)e^{iax}\]	\[\widehat{f} \left(\xi - \frac{a}{2\pi}\right)\]	\[\widehat{f}(\omega - a)\]	\[\widehat{f}(\omega - a)\]	Shift in frequency domain, dual of 102
104	\[f(a x)\]	\[\frac{1}{\|a\|} \widehat{f}\left( \frac{\xi}{a} \right)\]	\[\frac{1}{\|a\|} \widehat{f}\left( \frac{\omega}{a} \right)\]	\[\frac{1}{\|a\|} \widehat{f}\left( \frac{\omega}{a} \right)\]	Scaling in the time domain. If \[{{abs\|a}}\] is large, then \[f(ax)\] is concentrated around 0 and \[\frac{1}{\|a\|}\hat{f} \left( \frac{\omega}{a} \right)\] spreads out and flattens.
105	\[\widehat {f_n}(x)\]	\[\widehat {f_1}(x) \ \stackrel{\mathcal{F}_1}{\longleftrightarrow}\ f(-\xi)\]	\[\widehat {f_2}(x) \ \stackrel{\mathcal{F}_2}{\longleftrightarrow}\ f(-\omega)\]	\[\widehat {f_3}(x) \ \stackrel{\mathcal{F}_3}{\longleftrightarrow}\ 2\pi f(-\omega)\]	The same transform is applied twice, but x replaces the frequency variable (ξ or ω) after the first transform.
106	\[\frac{d^n f(x)}{dx^n}\]	\[(i 2\pi \xi)^n \widehat{f}(\xi)\]	\[(i\omega)^n \widehat{f}(\omega)\]	\[(i\omega)^n \widehat{f}(\omega)\]	n^th-order derivative. As \[f\] is a [[Schwartz space\|Schwartz function]]
106.5	\[\int_{-\infty}^{x} f(\tau) d \tau\]	\[\frac{\widehat{f}(\xi)}{i 2 \pi \xi} + C \, \delta(\xi)\]	\[\frac{\widehat{f} (\omega)}{i\omega} + \sqrt{2 \pi} C \delta(\omega)\]	\[\frac{\widehat{f} (\omega)}{i\omega} + 2 \pi C \delta(\omega)\]	Integration.^[1] Note: \[\delta\] is the [[Dirac delta function]] and \[C\] is the average ([[DC component\|DC]]) value of \[f(x)\] such that \[\int_{-\infty}^\infty (f(x) - C) \, dx = 0\]
107	\[x^n f(x)\]	\[\left (\frac{i}{2\pi}\right)^n \frac{d^n \widehat{f}(\xi)}{d\xi^n}\]	\[i^n \frac{d^n \widehat{f}(\omega)}{d\omega^n}\]	\[i^n \frac{d^n \widehat{f}(\omega)}{d\omega^n}\]	This is the dual of 106
108	\[(f * g)(x)\]	\[\widehat{f}(\xi) \widehat{g}(\xi)\]	\[\sqrt{2\pi}\ \widehat{f}(\omega) \widehat{g}(\omega)\]	\[\widehat{f}(\omega) \widehat{g}(\omega)\]	The notation \[f * g\] denotes the [[convolution]] of \[f\] and \[g\] — this rule is the [[convolution theorem]]
109	\[f(x) g(x)\]	\[\left(\widehat{f} * \widehat{g}\right)(\xi)\]	\[ \frac{1}{\sqrt{2\pi}} \left(\widehat{f} * \widehat{g}\right)(\omega) \]	\[\frac{1}{2\pi}\left(\widehat{f} * \widehat{g}\right)(\omega)\]	This is the dual of 108
110	For \[f(x)\] purely real	\[\widehat{f}(-\xi) = \overline{\widehat{f}(\xi)}\]	\[\widehat{f}(-\omega) = \overline{\widehat{f}(\omega)}\]	\[\widehat{f}(-\omega) = \overline{\widehat{f}(\omega)}\]	Hermitian symmetry. \[\overline{z}\] indicates the [[complex conjugate]].
113	For \[f(x)\] purely imaginary	\[\widehat{f}(-\xi) = -\overline{\widehat{f}(\xi)}\]	\[\widehat{f}(-\omega) = -\overline{\widehat{f}(\omega)}\]	\[\widehat{f}(-\omega) = -\overline{\widehat{f}(\omega)}\]	\[\overline{z}\] indicates the [[complex conjugate]].
114	\[\overline{f(x)}\]	\[\overline{\widehat{f}(-\xi)}\]	\[\overline{\widehat{f}(-\omega)}\]	\[\overline{\widehat{f}(-\omega)}\]	[[Complex conjugation]], generalization of 110 and 113
115	\[f(x) \cos (a x)\]	\[\frac{\widehat{f}\left(\xi - \frac{a}{2\pi}\right)+\widehat{f}\left(\xi+\frac{a}{2\pi}\right)}{2}\]	\[\frac{\widehat{f}(\omega-a)+\widehat{f}(\omega+a)}{2}\]	\[\frac{\widehat{f}(\omega-a)+\widehat{f}(\omega+a)}{2}\]	This follows from rules 101 and 103 using [[Euler's formula]]: \[\cos(a x) = \frac{e^{i a x} + e^{-i a x}}{2}.\]
116	\[f(x)\sin( ax)\]	\[\frac{\widehat{f}\left(\xi-\frac{a}{2\pi}\right)-\widehat{f}\left(\xi+\frac{a}{2\pi}\right)}{2i}\]	\[\frac{\widehat{f}(\omega-a)-\widehat{f}(\omega+a)}{2i}\]	\[\frac{\widehat{f}(\omega-a)-\widehat{f}(\omega+a)}{2i}\]	This follows from 101 and 103 using [[Euler's formula]]: \[\sin(a x) = \frac{e^{i a x} - e^{-i a x}}{2i}.\]

^[1] The Integration Property of the Fourier Transform

	Function	Fourier transform unitary, ordinary frequency	Fourier transform unitary, angular frequency	Fourier transform non-unitary, angular frequency	Remarks
	\[ f(x) \]	\[ \begin{align} &\hat{f}(\xi) \triangleq \hat f_1(\xi) \\&= \int_{-\infty}^\infty f(x) e^{-i 2\pi \xi x}\, dx \end{align} \]	\[ \begin{align} &\hat{f}(\omega) \triangleq \hat f_2(\omega) \\&= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align} \]	\[ \begin{align} &\hat{f}(\omega) \triangleq \hat f_3(\omega) \\&= \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align} \]	Definitions
201	\[ \operatorname{rect}(a x) \]	\[ \frac{1}{\|a\|}\, \operatorname{sinc}\left(\frac{\xi}{a}\right) \]	\[ \frac{1}{\sqrt{2 \pi a^2}}\, \operatorname{sinc}\left(\frac{\omega}{2\pi a}\right) \]	\[ \frac{1}{\|a\|}\, \operatorname{sinc}\left(\frac{\omega}{2\pi a}\right) \]	The rectangular pulse and the normalized sinc function, here defined as \[ 1=\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} \]
202	\[ \operatorname{sinc}(a x) \]	\[ \frac{1}{\|a\|}\, \operatorname{rect}\left(\frac{\xi}{a} \right) \]	\[ \frac{1}{\sqrt{2\pi a^2}}\, \operatorname{rect}\left(\frac{\omega}{2 \pi a}\right) \]	\[ \frac{1}{\|a\|}\, \operatorname{rect}\left(\frac{\omega}{2 \pi a}\right) \]	Dual of rule 201. The rectangular function is an ideal low-pass filter, and the sinc function is the non-causal impulse response of such a filter. The sinc function is defined here as \[ 1=\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} \]
203	\[ \operatorname{sinc}^2 (a x) \]	\[ \frac{1}{\|a\|}\, \operatorname{tri} \left( \frac{\xi}{a} \right) \]	\[ \frac{1}{\sqrt{2\pi a^2}}\, \operatorname{tri} \left( \frac{\omega}{2\pi a} \right) \]	\[ \frac{1}{\|a\|}\, \operatorname{tri} \left( \frac{\omega}{2\pi a} \right) \]	The function \[ \text{tri}(x) \] is the triangular function
204	\[ \operatorname{tri} (a x) \]	\[ \frac{1}{\|a\|}\, \operatorname{sinc}^2 \left( \frac{\xi}{a} \right) \]	\[ \frac{1}{\sqrt{2\pi a^2}} \, \operatorname{sinc}^2 \left( \frac{\omega}{2\pi a} \right) \]	\[ \frac{1}{\|a\|} \, \operatorname{sinc}^2 \left( \frac{\omega}{2\pi a} \right) \]	Dual of rule 203.
205	\[ e^{- a x} u(x) \]	\[ \frac{1}{a + i 2\pi \xi} \]	\[ \frac{1}{\sqrt{2 \pi} (a + i \omega)} \]	\[ \frac{1}{a + i \omega} \]	The function \[ u(x) \] is the Heaviside unit step function and \[ a > 0 \].
206	\[ e^{-\alpha x^2} \]	\[ \sqrt{\frac{\pi}{\alpha}}\, e^{-\frac{(\pi \xi)^2}{\alpha}} \]	\[ \frac{1}{\sqrt{2 \alpha}}\, e^{-\frac{\omega^2}{4 \alpha}} \]	\[ \sqrt{\frac{\pi}{\alpha}}\, e^{-\frac{\omega^2}{4 \alpha}} \]	This shows that, for the unitary Fourier transforms, the Gaussian function \[ e^{−αx^2} \] is its own Fourier transform for some choice of \[ α \]. For this to be integrable we must have \[ Re(α) > 0 \].
208	\[ e^{-a\|x\|} \]	\[ \frac{2 a}{a^2 + 4 \pi^2 \xi^2} \]	\[ \sqrt{\frac{2}{\pi}} \, \frac{a}{a^2 + \omega^2} \]	\[ \frac{2a}{a^2 + \omega^{2}} \]	For \[ Re(a) > 0 \]. That is, the Fourier transform of a two-sided decaying exponential function is a Lorentzian function.
209	\[ \operatorname{sech}(a x) \]	\[ \frac{\pi}{a} \operatorname{sech} \left( \frac{\pi^2}{ a} \xi \right) \]	\[ \frac{1}{a}\sqrt{\frac{\pi}{2}} \operatorname{sech}\left( \frac{\pi}{2 a} \omega \right) \]	\[ \frac{\pi}{a}\operatorname{sech}\left( \frac{\pi}{2 a} \omega \right) \]	Hyperbolic secant is its own Fourier transform
210	\[ e^{-\frac{a^2 x^2}2} H_n(a x) \]	\[ \frac{\sqrt{2\pi}(-i)^n}{a} e^{-\frac{2\pi^2\xi^2}{a^2}} H_n\left(\frac{2\pi\xi}a\right) \]	\[ \frac{(-i)^n}{a} e^{-\frac{\omega^2}{2 a^2}} H_n\left(\frac \omega a\right) \]	\[ \frac{(-i)^n \sqrt{2\pi}}{a} e^{-\frac{\omega^2}{2 a^2}} H_n\left(\frac \omega a \right) \]	\[ H_n \] is the \[ n \]th-order Hermite polynomial. If \[ a = 1 \] then the Gauss–Hermite functions are eigenfunctions of the Fourier transform operator. For a derivation, see Hermite polynomial. The formula reduces to 206 for \[ n = 0 \].

	Function	Fourier transform unitary, ordinary frequency	Fourier transform unitary, angular frequency	Fourier transform non-unitary, angular frequency	Remarks
	\[ f(x) \]	\[ \begin{align} &\hat{f}(\xi) \triangleq \hat f_1(\xi) \\&= \int_{-\infty}^\infty f(x) e^{-i 2\pi \xi x}\, dx \end{align} \]	\[ \begin{align} &\hat{f}(\omega) \triangleq \hat f_2(\omega) \\&= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align} \]	\[ \begin{align} &\hat{f}(\omega) \triangleq \hat f_3(\omega) \\&= \int_{-\infty}^\infty f(x) e^{-i \omega x}\, dx \end{align} \]	Definitions
301	\[ 1 \]	\[ \delta(\xi) \]	\[ \sqrt{2\pi}\, \delta(\omega) \]	\[ 2\pi\delta(\omega) \]	The distribution \[ ''δ''(''ξ'') \] denotes the [[Dirac delta function]].
302	\[ \delta(x) \]	\[ 1 \]	\[ \frac{1}{\sqrt{2\pi}} \]	\[ 1 \]	Dual of rule 301.
303	\[ e^{i a x} \]	\[ \delta\left(\xi - \frac{a}{2\pi}\right) \]	\[ \sqrt{2 \pi}\, \delta(\omega - a) \]	\[ 2 \pi\delta(\omega - a) \]	This follows from 103 and 301.
304	\[ \cos (a x) \]	\[ \frac{\delta\left(\xi - \frac{a}{2\pi}\right)+\delta\left(\xi+\frac{a}{2\pi}\right)}{2} \]	\[ \sqrt{2 \pi}\,\frac{\delta(\omega-a)+\delta(\omega+a)}{2} \]	\[ \pi\left(\delta(\omega-a)+\delta(\omega+a)\right) \]	This follows from rules 101 and 303 using [[Euler's formula]]: \[ \cos(a x) = \frac{e^{i a x} + e^{-i a x}}{2}. \]
305	\[ \sin( ax) \]	\[ \frac{\delta\left(\xi-\frac{a}{2\pi}\right)-\delta\left(\xi+\frac{a}{2\pi}\right)}{2i} \]	\[ \sqrt{2 \pi}\,\frac{\delta(\omega-a)-\delta(\omega+a)}{2i} \]	\[ -i\pi\bigl(\delta(\omega-a)-\delta(\omega+a)\bigr) \]	This follows from 101 and 303 using \[ \sin(a x) = \frac{e^{i a x} - e^{-i a x}}{2i}. \]
306	\[ \cos \left( a x^2 \right) \]	\[ \sqrt{\frac{\pi}{a}} \cos \left( \frac{\pi^2 \xi^2}{a} - \frac{\pi}{4} \right) \]	\[ \frac{1}{\sqrt{2 a}} \cos \left( \frac{\omega^2}{4 a} - \frac{\pi}{4} \right) \]	\[ \sqrt{\frac{\pi}{a}} \cos \left( \frac{\omega^2}{4a} - \frac{\pi}{4} \right) \]	This follows from 101 and 207 using \[ \cos(a x^2) = \frac{e^{i a x^2} + e^{-i a x^2}}{2}. \]
307	\[ \sin \left( a x^2 \right) \]	\[ - \sqrt{\frac{\pi}{a}} \sin \left( \frac{\pi^2 \xi^2}{a} - \frac{\pi}{4} \right) \]	\[ \frac{-1}{\sqrt{2 a}} \sin \left( \frac{\omega^2}{4 a} - \frac{\pi}{4} \right) \]	\[ -\sqrt{\frac{\pi}{a}}\sin \left( \frac{\omega^2}{4a} - \frac{\pi}{4} \right) \]	This follows from 101 and 207 using \[ \sin(a x^2) = \frac{e^{i a x^2} - e^{-i a x^2}}{2i}. \]
308	\[ e^{-\pi i\alpha x^2} \]	\[ \frac{1}{\sqrt{\alpha}}\, e^{-i\frac{\pi}{4}} e^{i\frac{\pi \xi^2}{\alpha}} \]	\[ \frac{1}{\sqrt{2\pi \alpha}}\, e^{-i\frac{\pi}{4}} e^{i\frac{\omega^2}{4\pi \alpha}} \]	\[ \frac{1}{\sqrt{\alpha}}\, e^{-i\frac{\pi}{4}} e^{i\frac{\omega^2}{4\pi \alpha}} \]	Here it is assumed \[ \alpha \] is real. For the case that alpha is complex see table entry 206 above.
309	\[ x^n \]	\[ \left(\frac{i}{2\pi}\right)^n \delta^{(n)} (\xi) \]	\[ i^n \sqrt{2\pi} \delta^{(n)} (\omega) \]	\[ 2\pi i^n\delta^{(n)} (\omega) \]	Here, \[ n \] is a [[natural number]] and \[ ''δ''{{isup\|(''n'')}}\left(\xi\right) \] is the \[ n \]th distribution derivative of the Dirac delta function. This rule follows from rules 107 and 301. Combining this rule with 101, we can transform all [[polynomial]]s.
310	\[ \delta^{(n)}(x) \]	\[ (i 2\pi \xi)^n \]	\[ \frac{(i\omega)^n}{\sqrt{2\pi}} \]	\[ (i\omega)^n \]	Dual of rule 309. \[ ''δ''{{isup\|(''n'')}}\left(\xi\right) \] is the \[ n \]th distribution derivative of the Dirac delta function. This rule follows from 106 and 302.
311	\[ \frac{1}{x} \]	\[ -i\pi\sgn(\xi) \]	\[ -i\sqrt{\frac{\pi}{2}}\sgn(\omega) \]	\[ -i\pi\sgn(\omega) \]	Here \[ sgn(\xi) \] is the [[sign function]]. Note that \[ \frac{1}{x} \] is not a distribution. It is necessary to use the [[Cauchy principal value]] when testing against [[Schwartz functions]]. This rule is useful in studying the [[Hilbert transform]].
312	\[ \begin{align} &\frac{1}{x^n} \\ &:= \frac{(-1)^{n-1}}{(n-1)!}\frac{d^n}{dx^n}\log \|x\| \end{align} \]	\[ -i\pi \frac{(-i 2\pi \xi)^{n-1}}{(n-1)!} \sgn(\xi) \]	\[ -i\sqrt{\frac{\pi}{2}}\, \frac{(-i\omega)^{n-1}}{(n-1)!}\sgn(\omega) \]	\[ -i\pi \frac{(-i\omega)^{n-1}}{(n-1)!}\sgn(\omega) \]	\[ \frac{1}{x^n} \] is the [[homogeneous distribution]] defined by the distributional derivative \[ \frac{(-1)^{n-1}}{(n-1)!}\frac{d^n}{dx^n}\log\|x\| \]
313	\[ \|x\|^\alpha \]	\[ -\frac{2\sin\left(\frac{\pi\alpha}{2}\right)\Gamma(\alpha+1)}{\|2\pi\xi\|^{\alpha+1}} \]	\[ \frac{-2}{\sqrt{2\pi}}\, \frac{\sin\left(\frac{\pi\alpha}{2}\right)\Gamma(\alpha+1)}{\|\omega\|^{\alpha+1}} \]	\[ -\frac{2\sin\left(\frac{\pi\alpha}{2}\right)\Gamma(\alpha+1)}{\|\omega\|^{\alpha+1}} \]	This formula is valid for \[ 0 > \alpha > -1 \]. For \[ \alpha > 0 \] some singular terms arise at the origin that can be found by differentiating 320. If \[ Re \alpha > -1 \], then \[ \|x\|^\alpha \] is a locally integrable function, and so a tempered distribution. The function \[ \alpha \mapsto \|x\|^\alpha \] is a holomorphic function from the right half-plane to the space of tempered distributions. It admits a unique meromorphic extension to a tempered distribution, also denoted \[ \|x\|^\alpha \] for \[ \alpha \neq -1, -3, ... \] (See [[homogeneous distribution]].)
	\[ \frac{1}{\sqrt{\|x\|}} \]	\[ \frac{1}{\sqrt{\|\xi\|}} \]	\[ \frac{1}{\sqrt{\|\omega\|}} \]	\[ \frac{\sqrt{2\pi}}{\sqrt{\|\omega\|}} \]	Special case of 313.
314	\[ \sgn(x) \]	\[ \frac{1}{i\pi \xi} \]	\[ \sqrt{\frac{2}{\pi}} \frac{1}{i\omega} \]	\[ \frac{2}{i\omega} \]	The dual of rule 311. This time the Fourier transforms need to be considered as a [[Cauchy principal value]].
315	\[ u(x) \]	\[ \frac{1}{2}\left(\frac{1}{i \pi \xi} + \delta(\xi)\right) \]	\[ \sqrt{\frac{\pi}{2}} \left( \frac{1}{i \pi \omega} + \delta(\omega)\right) \]	\[ \pi\left( \frac{1}{i \pi \omega} + \delta(\omega)\right) \]	The function \[ u(x) \] is the Heaviside [[Heaviside step function\|unit step function]]; this follows from rules 101, 301, and 314.
316	\[ \sum_{n=-\infty}^{\infty} \delta (x - n T) \]	\[ \frac{1}{T} \sum_{k=-\infty}^{\infty} \delta \left( \xi -\frac{k }{T}\right) \]	\[ \frac{\sqrt{2\pi }}{T}\sum_{k=-\infty}^{\infty} \delta \left( \omega -\frac{2\pi k}{T}\right) \]	\[ \frac{2\pi}{T}\sum_{k=-\infty}^{\infty} \delta \left( \omega -\frac{2\pi k}{T}\right) \]	This function is known as the [[Dirac comb]] function. This result can be derived from 302 and 102, together with the fact that \[ \begin{align} & \sum_{n=-\infty}^{\infty} e^{inx} \\ = {}& 2\pi\sum_{k=-\infty}^{\infty} \delta(x+2\pi k) \end{align} \] as distributions.
317	\[ J_0 (x) \]	\[ \frac{2\, \operatorname{rect}(\pi\xi)}{\sqrt{1 - 4 \pi^2 \xi^2}} \]	\[ \sqrt{\frac{2}{\pi}} \, \frac{\operatorname{rect}\left(\frac{\omega}{2}\right)}{\sqrt{1 - \omega^2}} \]	\[ \frac{2\,\operatorname{rect}\left(\frac{\omega}{2}\right)}{\sqrt{1 - \omega^2}} \]	The function \[ J_0(x) \] is the zeroth order [[Bessel function]] of first kind.

Attached file

이 게시물을..

25

세상의모든계산기
계산기는 거들 뿐
혹은
계산기를 거들 뿐

글쓴이의 서명작성글 감추기

댓글 쓰기 에디터 사용하기 닫기

view_headline 목록

SEARCH

푸리에 급수 테이블 , 푸리에 변환 테이블, Fourier Series Table, Fourier Transform Table

Functional relationships, one-dimensional

세상의모든계산기 님의 최근 글

세상의모든계산기 님의 최근 댓글