- 일반(쌀집) 계산기
[일반 계산기] 쌀집 계산기로도 방정식의 미지수를 구할 수 있을까?
1. 일반 계산기로 방정식의 해 구하기 ?
일반 계산기는 해를 구하는 기능이 없기 때문에, 손으로 방정식을 풀어서 답을 구하는 방법을 사용해야 합니다.
방정식이 단순해서 x=□□□□ (사칙연산)꼴로 깔끔하게 정리될 수 있다면,
□□□□ 부분을 일반 계산기에 입력해서 결과를 얻어낼 수 있겠습니다만,
이 때도 소숫점 지수가 나온다거나 한다면
일반 계산기로 답을 구하는 것이 (현실적으로) 불가능할 수 있습니다.
2. 정리해도 풀 수 없는 경우
지금 100만원을 빌려주고 5년 후 150만원을 받는 경우, 연이자율(r)은?
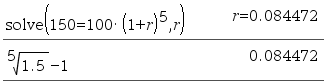
r에 대해 정리한다고 해도 5제곱근(=0.2 제곱)을 구하기가 쉽지 않아서 일반 계산기로는 (현실적으로) 정답을 찾을 수 없습니다.
다만, 어느정도의 오차를 감안하고 근사값으로 만족한다면 아래와 같이 찾아볼 수는 있습니다.
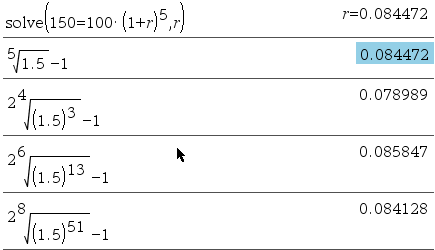
ㄴ 자세한 방법은 다음 링크 댓글 참고 : http://www.allcalc.org/6866#comment_14500
3. 정리조차 되지 않는 경우
매년말 12만원씩 입금하여 6년말에 100만원을 받게 될 때, 이자율을 구하면?
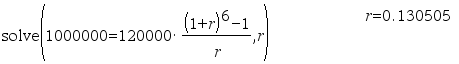
이런 방정식은 아예 r=□□□□ 꼴로 간단하게 정리조차 되지 않습니다. 이런 문제에서는 일반 계산기로는 해를 단번에 구해낼 수 없습니다.
그나마 할 수 있는 최선의 방법은 Trial and Error (시행착오법) 입니다.
대략적인 이자율(r')을 추정해서 FVAF(또는 PVAF) 를 구해보고,
그 결과 분석을 바탕으로 더 정확한 새로운 추정값(r'') 으로 시도해 보고,
또 그 결과 분석을 바탕으로 더더 정확한 새로운 추정값(r''') 로 시도해 보고,
반복에 반복을 거듭해서 r 에 가까워지는 방법입니다.
당연히 시간이 오래 걸리고, 정확한 값도 찾을 수 없습니다. 그래서 보간법을 보조로 써주는 것이 좋습니다.
FVAF 처럼 GT 기능으로 그 값을 구할 수 있는 경우에는 그나마 이렇게 시행착오법이라도 쓸 수 있지만, 기타 방정식이 조금만 복잡해져도 일반 계산기의 힘으로 그 해를 찾는 방법은 없습니다.
어쨌건 결론은...
일반 계산기로는 답을 간단하게 못구하기 때문에, 일반 계산기만을 사용하는 시험에서는 이런식으로 문제가 출제되지 않습니다.
최소한 이런 방식의 계산 없이도 답을 찾을 수 있는 추가조건이 문제에 제시될 것입니다.
ㄴ 출처 : https://m.cafe.daum.net/account2000/7BL/40579?listURI=%2Faccount2000%2F7BL
만약, 유효 이자율을 직접 구하라고 시험에 나왔다면 제보 바랍니다.
댓글 10
-
-
-
예제2)
https://kin.naver.com/qna/detail.naver?d1id=4&dirId=40402&docId=459915389&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=1&search_sort=3&spq=0
3년 만기 10만원권 사채 (액면 이자율 7%, 이자액 연 7,000원 후급) 의 발행금액이 91,372 원일 때 유효이자율은?
- 10만원보다 싼 가격에 발행 = 할인 발행 = 유효 이자율은 7%보다 높다
- 8% 라고 치고 계산 : 97,423
- 9% 라고 치고 계산 : 94,937
- 10% 라고 치고 계산 : 92,539
- 11% 라고 치고 계산 : 90,225
- 유효 이자율은 10%~11% 사이 라는 것을 알 수 있다. 보간법으로 계산
- (91,372 - 90,225) ÷ (92,539 - 90,225) = 0.49567847882455
- 따라서 유효 이자율은 10.5%
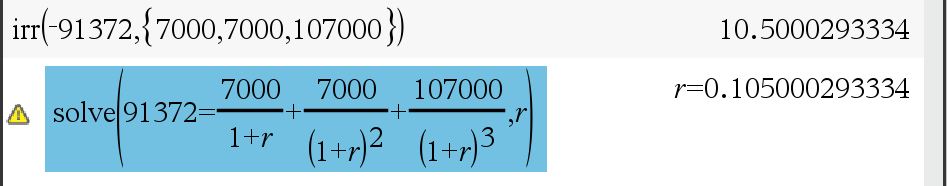
-
-
-
8%, 9%, 10%, 11% 네번 계산하기 귀찮은데
8% 라고 치고 계산해 97,423
15% 라고 치고 계산해 81,734구간을 넓게 구하고
보간법으로 답을 구한다면?
- (91372-81734)÷(97423-81734) = 0.70178897047952
- (15-8) (%)을 곱하면 4.30 (%)이 나오는데
- 이걸 8%에서 더하는 것이 아니고, 15%에서 빼야 함
- 15% - 4.30% = 10.7 %
얼추 비슷하긴 하지만, (출제자가 요구하는) 답 10.5% 와는 차이가 있다.
(하지만 객관식이면 맞출 수는 있을 것!)
구간이 커지면 오차도 커지면서 구해야 하는 답이 나오지 않게 되니 주의해야 한다.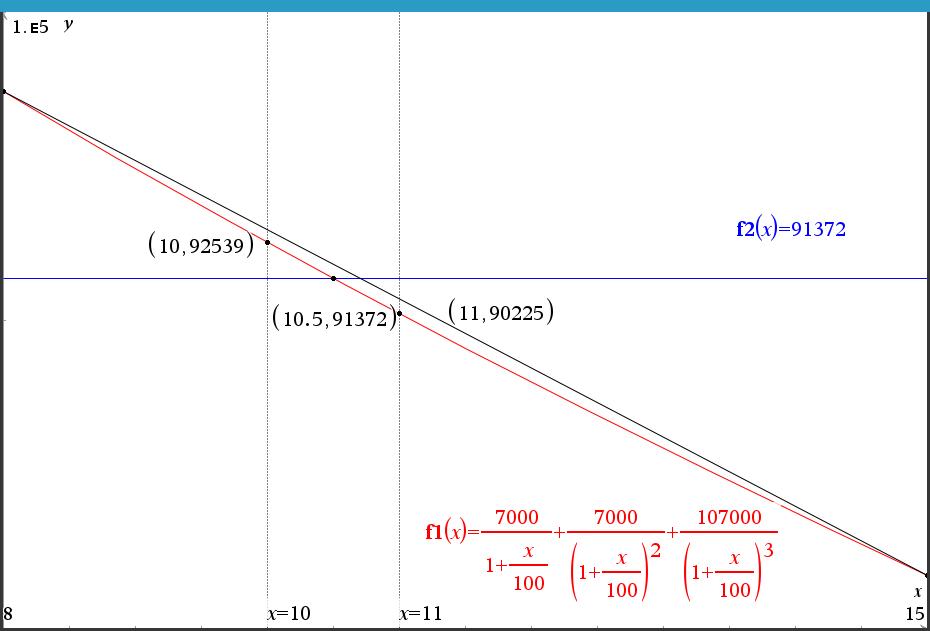
-
-
-
방법이 이것 뿐일까? 대안은 없나?
현재가치로 나누는 것 말고, 미래가치로 곱하면 좀 계산이 쉬워지나?
쌀집 계산기로는 계산하는 것은 별반 차이가 없긴 한데...
-
-
-
만약 오차를 감안한다고 가정했을 때 (trial and error보다) 쉽게 계산하는 방법을 만들 수 있나?
오차를 감안하는 위험을 안고 있기 때문에,
오차를 최소화할 수 있는 장치가 반드시 필요하다.1년 후(작은 값) / 2년 후(작은 값) / 3년 후 107,000원(큰값)을 모조리 현재가치로 넘기는 것에 비하면
1년 후 7,000원(작은값)과 2년 후 7,000원(작은값) 만을 미래가치로 로 넘기는 것이오차 수준이 훨씬 적다. OK
-
-
-
n제곱근법
그런 개념(오차 감안)을 바탕으로 계산을 해 보자.
1. 유효 이자율은 계산 없이 정확하게 알 수는 없지만,
"7% 보다 높다"는 것은 안다.
그래서 8%로 추정 이자율을 가정하자
(추정 이자율이 실제 유효 이자율에 가까울 수록 오차는 줄어든다)
2. 채권으로 인한 현금흐름의 미래가치(FV)를 계산
7,000*(1.08)^2 + 7,000*1.08 + 7,000 + 100,000 = 122724.8
3. 투자대비 수익률 계산
122724.8 ÷ 91372 ≒ 1.3431 = (1+r)^3
4. r' 계산
r'= 1.3431^(1/3) -1 ≒ 0.1033 = 10.33%
쌀집 계산기로 세제곱근 계산은 https://allcalc.org/2629
-
-
-
예제3) n제곱근법 이용

https://kin.naver.com/qna/detail.naver?d1id=4&dirId=40402&docId=467327574&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=1&search_sort=3&spq=0
(1회차)
1. 추정이자율 11%
2. 채권 현금흐름의 미래가치 계산
100000*1.11^2 + 100000*1.11 + 1100000 = 13342103. 투자대비 수익률 계산
1334210 ÷ 885840 = 1.5062 = (1+r')^3* 쌀집 계산기로 세제곱근 계산은 https://allcalc.org/2629 참고
4. r' 계산
r' = 0.1463 = 14.63%
추정이자율(11%) < r'(14.63%) 이므로 실제 유효이자율은 r'보다 높다.
객관식이면 (①~⑤ 보기를 통해) 여기서 찍어서 맞출 수도 있다.
주관식이라도 처음 추정이자율이 실제 유효이자율에 가깝다면 한번에 정답에 가까운 값을 얻을 수 있다.이번 경우처럼 추정이자율과 실제이자유의 차이가 조금(5%) 있는 경우
주관식이면 위 과정(1~4)를 한 번 더 반복해(2회차) 정답에 매우 가까운 값을 얻을 수 있다.ㄴ 현실적으로 그런 문제는 안 낸다고 봐야함. 따라서 (아래) 2회차 계산까지 하는 것은 시간낭비.
(2회차)
1. 추정이자율 15% (14.63% 보다 높은거 아니까 15%로 추정)
2. 채권 현금흐름의 미래가치 계산
100000*1.15^2 + 100000*1.15 + 1100000 = 13472503. 투자대비 수익률 계산
1347250 ÷ 885840 = 1.5209 = (1+r')^34. r' 계산
r' = 0.1500 = 15%
-
-
-
예시) 사채의 시장 이자율
https://kin.naver.com/qna/detail.naver?d1id=11&dirId=111301&docId=475758324
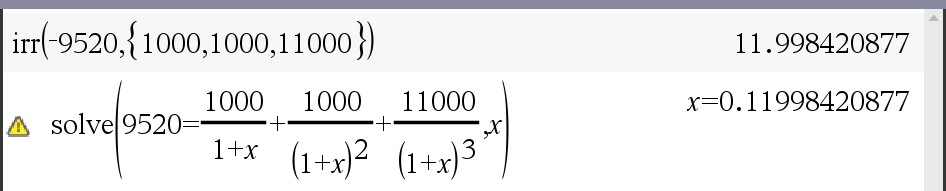
1) 이자율 추정
10000 원에 이자 1000 원이니 일단 10%로 추정2) 매기 수익 현금 흐름을 미래(!) 가치로 전환
1000*1.1*1.1 + 1000*1.1 + 11000 = 13,3103) 3년간 누적 수익률 추정
13,310/9520 = 1.3981092436975
4) 1년간 수익률(r') 추정
(1+r')^3 = 1.39810924369755) 세제곱근 계산
https://allcalc.org/2629 - 방법1 : 정수 세제곱근
【√】【√】 방법 4회 반복하면?
(1+r') ≒ 1.1176972842958r' ≒ 11.77%
처음 추정한 이자율(10%)과 대충 추정한 이자율(11.77%) 이 큰 차이가 없으므로
이자율을 12%로 대충 때려 맞출 수도 있고,
원리 원칙대로 12%로 다시 수정해서 처음부터 계산을 다시 시작할 수도 있겠지만...
- 그만큼 시간이 낭비되기 때문에 적당히 감으로 때려맞추는 능력이 필요.
- 처음 추정한 이자율은 10% 보다 높을 것은 자명하기 때문에 11% 로 시작할 수 있으며 그러면 추정치가 더 정확해 짐. (동일한 계산과정이면 r'=11.86%)
-
-
-
계산기 버튼 입력은 계산기마다 다르지만,
대충 흐름을 알기 위해 적어 보면
- 이자율 추정 : 10%
- 현금흐름의 미래가치
1.1 × 1000 = 1100
× 1.1 = 1210
Recall GT = 2310
2310 + 11000 = 13310 - 3년 누적 수익률
13310 ÷ 9520 = 1.3981092436975 - 1년간 추정 수익률(r') 계산
M += 1.3981092436975
(√1.3981092436975 = 1.1824166963036)
(√1.1824166963036 = 1.0873898547916)
1.0873898547916 × (Recall M=1.3981092436975) = 1.5202898074870
(√1.5202898074870 = 1.2330003274481)
(√1.2330003274481 = 1.1104054788446)
1.1104054788446 × (Recall M=1.3981092436975) = 1.5524681642250
(√1.5524681642250 = 1.2459808041158)
(√1.2459808041158 = 1.1162351025280)
1.1162351025280 × (Recall M=1.3981092436975) = 1.5606186149840
(√1.5606186149840 = 1.2492472193221)
(√1.2492472193221 = 1.1176972842958)
-
-
-
12%로 다시 계산하면
MC
1.12 × 1000 = 1120.00
× 1.12 = 1254.4000
Recall GT = 2374.4000
2374.4000 + 11000 = 13374.4000
13374.4000 ÷ 9520 = 1.4048739495798
M += 1.4048739495798
(√1.4048739495798 = 1.1852737867598)
(√1.1852737867598 = 1.0887028000147)
1.0887028000147 × (Recall M = 1.4048739495798) = 1.5294902025752
(√1.5294902025752 = 1.2367255971214)
(√1.2367255971214 = 1.1120816503843)
1.1120816503843 × (Recall M = 1.4048739495798) = 1.5623345404306
(√1.5623345404306 = 1.2499338144200)
(√1.2499338144200 = 1.1180043892669)
1.1180043892669 × (Recall M = 1.4048739495798) = 1.5706552419969
(√1.5706552419969 = 1.2532578513606)
(√1.2532578513606 = 1.1194899960967)
-


예제1)
http://kin.naver.com/qna/detail.nhn?d1id=4&dirId=40402&docId=250214996&page=1#answer1
식을 i 에 대해 정리하여 계산기로 계산