[일반 계산기] 쌀집 계산기로도 방정식의 미지수를 구할 수 있을까?
1. 일반 계산기로 방정식의 해 구하기 ?
일반 계산기는 해를 구하는 기능이 없기 때문에, 손으로 방정식을 풀어서 답을 구하는 방법을 사용해야 합니다.
방정식이 단순해서 x=□□□□ (사칙연산)꼴로 깔끔하게 정리될 수 있다면,
□□□□ 부분을 일반 계산기에 입력해서 결과를 얻어낼 수 있겠습니다만,
이 때도 소숫점 지수가 나온다거나 한다면
일반 계산기로 답을 구하는 것이 (현실적으로) 불가능할 수 있습니다.
2. 정리해도 풀 수 없는 경우
지금 100만원을 빌려주고 5년 후 150만원을 받는 경우, 연이자율(r)은?
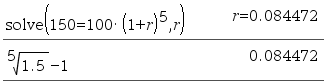
r에 대해 정리한다고 해도 5제곱근(=0.2 제곱)을 구하기가 쉽지 않아서 일반 계산기로는 (현실적으로) 정답을 찾을 수 없습니다.
다만, 어느정도의 오차를 감안하고 근사값으로 만족한다면 아래와 같이 찾아볼 수는 있습니다.
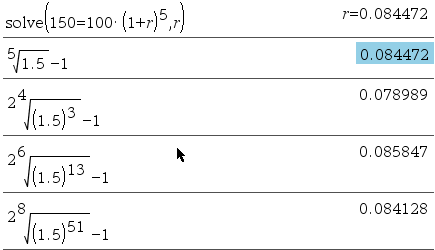
ㄴ 자세한 방법은 다음 링크 댓글 참고 : http://www.allcalc.org/6866#comment_14500
3. 정리조차 되지 않는 경우
매년말 12만원씩 입금하여 6년말에 100만원을 받게 될 때, 이자율을 구하면?
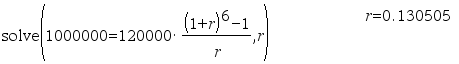
이런 방정식은 아예 r=□□□□ 꼴로 간단하게 정리조차 되지 않습니다. 이런 문제에서는 일반 계산기로는 해를 단번에 구해낼 수 없습니다.
그나마 할 수 있는 최선의 방법은 Trial and Error (시행착오법) 입니다.
대략적인 이자율(r')을 추정해서 FVAF(또는 PVAF) 를 구해보고,
그 결과 분석을 바탕으로 더 정확한 새로운 추정값(r'') 으로 시도해 보고,
또 그 결과 분석을 바탕으로 더더 정확한 새로운 추정값(r''') 로 시도해 보고,
반복에 반복을 거듭해서 r 에 가까워지는 방법입니다.
당연히 시간이 오래 걸리고, 정확한 값도 찾을 수 없습니다. 그래서 보간법을 보조로 써주는 것이 좋습니다.
FVAF 처럼 GT 기능으로 그 값을 구할 수 있는 경우에는 그나마 이렇게 시행착오법이라도 쓸 수 있지만, 기타 방정식이 조금만 복잡해져도 일반 계산기의 힘으로 그 해를 찾는 방법은 없습니다.
어쨌건 결론은...
일반 계산기로는 답을 간단하게 못구하기 때문에, 일반 계산기만을 사용하는 시험에서는 이런식으로 문제가 출제되지 않습니다.
최소한 이런 방식의 계산 없이도 답을 찾을 수 있는 추가조건이 문제에 제시될 것입니다.
ㄴ 출처 : https://m.cafe.daum.net/account2000/7BL/40579?listURI=%2Faccount2000%2F7BL
만약, 유효 이자율을 직접 구하라고 시험에 나왔다면 제보 바랍니다.
댓글10
-
세상의모든계산기
예제1)
http://kin.naver.com/qna/detail.nhn?d1id=4&dirId=40402&docId=250214996&page=1#answer1
식을 i 에 대해 정리하여 계산기로 계산

-
세상의모든계산기
예제2)
https://kin.naver.com/qna/detail.naver?d1id=4&dirId=40402&docId=459915389&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=1&search_sort=3&spq=0
3년 만기 10만원권 사채 (액면 이자율 7%, 이자액 연 7,000원 후급) 의 발행금액이 91,372 원일 때 유효이자율은?
- 10만원보다 싼 가격에 발행 = 할인 발행 = 유효 이자율은 7%보다 높다
- 8% 라고 치고 계산 : 97,423
- 9% 라고 치고 계산 : 94,937
- 10% 라고 치고 계산 : 92,539
- 11% 라고 치고 계산 : 90,225
- 유효 이자율은 10%~11% 사이 라는 것을 알 수 있다. 보간법으로 계산
- (91,372 - 90,225) ÷ (92,539 - 90,225) = 0.49567847882455
- 따라서 유효 이자율은 10.5%
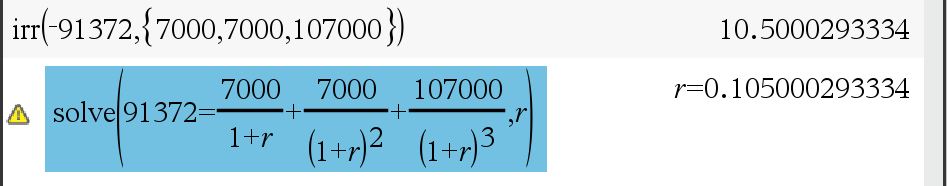
-
1
세상의모든계산기
8%, 9%, 10%, 11% 네번 계산하기 귀찮은데
8% 라고 치고 계산해 97,423
15% 라고 치고 계산해 81,734구간을 넓게 구하고
보간법으로 답을 구한다면?
- (91372-81734)÷(97423-81734) = 0.70178897047952
- (15-8) (%)을 곱하면 4.30 (%)이 나오는데
- 이걸 8%에서 더하는 것이 아니고, 15%에서 빼야 함
- 15% - 4.30% = 10.7 %
얼추 비슷하긴 하지만, (출제자가 요구하는) 답 10.5% 와는 차이가 있다.
(하지만 객관식이면 맞출 수는 있을 것!)
구간이 커지면 오차도 커지면서 구해야 하는 답이 나오지 않게 되니 주의해야 한다.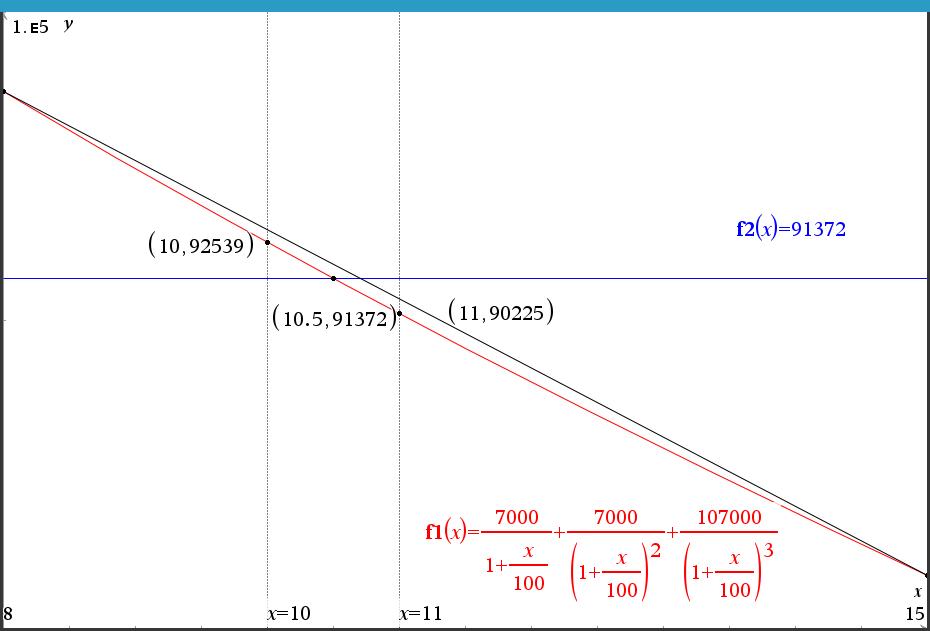
- 1
-
2
세상의모든계산기
만약 오차를 감안한다고 가정했을 때 (trial and error보다) 쉽게 계산하는 방법을 만들 수 있나?
오차를 감안하는 위험을 안고 있기 때문에,
오차를 최소화할 수 있는 장치가 반드시 필요하다.1년 후(작은 값) / 2년 후(작은 값) / 3년 후 107,000원(큰값)을 모조리 현재가치로 넘기는 것에 비하면
1년 후 7,000원(작은값)과 2년 후 7,000원(작은값) 만을 미래가치로 로 넘기는 것이오차 수준이 훨씬 적다. OK
-
3
세상의모든계산기
n제곱근법
그런 개념(오차 감안)을 바탕으로 계산을 해 보자.
1. 유효 이자율은 계산 없이 정확하게 알 수는 없지만,
"7% 보다 높다"는 것은 안다.
그래서 8%로 추정 이자율을 가정하자
(추정 이자율이 실제 유효 이자율에 가까울 수록 오차는 줄어든다)
2. 채권으로 인한 현금흐름의 미래가치(FV)를 계산
7,000*(1.08)^2 + 7,000*1.08 + 7,000 + 100,000 = 122724.8
3. 투자대비 수익률 계산
122724.8 ÷ 91372 ≒ 1.3431 = (1+r)^3
4. r' 계산
r'= 1.3431^(1/3) -1 ≒ 0.1033 = 10.33%
쌀집 계산기로 세제곱근 계산은 https://allcalc.org/2629
-
세상의모든계산기
예제3) n제곱근법 이용

https://kin.naver.com/qna/detail.naver?d1id=4&dirId=40402&docId=467327574&qb=6rOE7IKw6riw&enc=utf8§ion=kin.qna.all&rank=1&search_sort=3&spq=0
(1회차)
1. 추정이자율 11%
2. 채권 현금흐름의 미래가치 계산
100000*1.11^2 + 100000*1.11 + 1100000 = 13342103. 투자대비 수익률 계산
1334210 ÷ 885840 = 1.5062 = (1+r')^3* 쌀집 계산기로 세제곱근 계산은 https://allcalc.org/2629 참고
4. r' 계산
r' = 0.1463 = 14.63%
추정이자율(11%) < r'(14.63%) 이므로 실제 유효이자율은 r'보다 높다.
객관식이면 (①~⑤ 보기를 통해) 여기서 찍어서 맞출 수도 있다.
주관식이라도 처음 추정이자율이 실제 유효이자율에 가깝다면 한번에 정답에 가까운 값을 얻을 수 있다.이번 경우처럼 추정이자율과 실제이자유의 차이가 조금(5%) 있는 경우
주관식이면 위 과정(1~4)를 한 번 더 반복해(2회차) 정답에 매우 가까운 값을 얻을 수 있다.ㄴ 현실적으로 그런 문제는 안 낸다고 봐야함. 따라서 (아래) 2회차 계산까지 하는 것은 시간낭비.
(2회차)
1. 추정이자율 15% (14.63% 보다 높은거 아니까 15%로 추정)
2. 채권 현금흐름의 미래가치 계산
100000*1.15^2 + 100000*1.15 + 1100000 = 13472503. 투자대비 수익률 계산
1347250 ÷ 885840 = 1.5209 = (1+r')^34. r' 계산
r' = 0.1500 = 15% -
세상의모든계산기
예시) 사채의 시장 이자율
https://kin.naver.com/qna/detail.naver?d1id=11&dirId=111301&docId=475758324
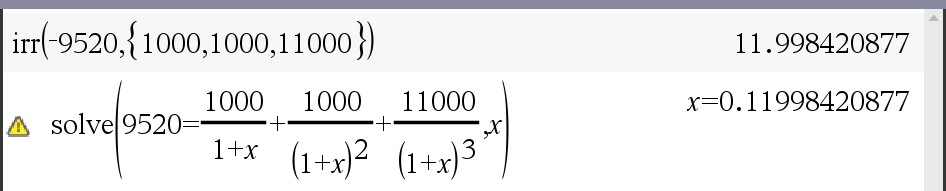
1) 이자율 추정
10000 원에 이자 1000 원이니 일단 10%로 추정2) 매기 수익 현금 흐름을 미래(!) 가치로 전환
1000*1.1*1.1 + 1000*1.1 + 11000 = 13,3103) 3년간 누적 수익률 추정
13,310/9520 = 1.3981092436975
4) 1년간 수익률(r') 추정
(1+r')^3 = 1.39810924369755) 세제곱근 계산
https://allcalc.org/2629 - 방법1 : 정수 세제곱근
【√】【√】 방법 4회 반복하면?
(1+r') ≒ 1.1176972842958r' ≒ 11.77%
처음 추정한 이자율(10%)과 대충 추정한 이자율(11.77%) 이 큰 차이가 없으므로
이자율을 12%로 대충 때려 맞출 수도 있고,
원리 원칙대로 12%로 다시 수정해서 처음부터 계산을 다시 시작할 수도 있겠지만...
- 그만큼 시간이 낭비되기 때문에 적당히 감으로 때려맞추는 능력이 필요.
- 처음 추정한 이자율은 10% 보다 높을 것은 자명하기 때문에 11% 로 시작할 수 있으며 그러면 추정치가 더 정확해 짐. (동일한 계산과정이면 r'=11.86%)
-
1
세상의모든계산기
계산기 버튼 입력은 계산기마다 다르지만,
대충 흐름을 알기 위해 적어 보면
- 이자율 추정 : 10%
- 현금흐름의 미래가치
1.1 × 1000 = 1100
× 1.1 = 1210
Recall GT = 2310
2310 + 11000 = 13310 - 3년 누적 수익률
13310 ÷ 9520 = 1.3981092436975 - 1년간 추정 수익률(r') 계산
M += 1.3981092436975
(√1.3981092436975 = 1.1824166963036)
(√1.1824166963036 = 1.0873898547916)
1.0873898547916 × (Recall M=1.3981092436975) = 1.5202898074870
(√1.5202898074870 = 1.2330003274481)
(√1.2330003274481 = 1.1104054788446)
1.1104054788446 × (Recall M=1.3981092436975) = 1.5524681642250
(√1.5524681642250 = 1.2459808041158)
(√1.2459808041158 = 1.1162351025280)
1.1162351025280 × (Recall M=1.3981092436975) = 1.5606186149840
(√1.5606186149840 = 1.2492472193221)
(√1.2492472193221 = 1.1176972842958)
-
2
세상의모든계산기
12%로 다시 계산하면
MC
1.12 × 1000 = 1120.00
× 1.12 = 1254.4000
Recall GT = 2374.4000
2374.4000 + 11000 = 13374.4000
13374.4000 ÷ 9520 = 1.4048739495798
M += 1.4048739495798
(√1.4048739495798 = 1.1852737867598)
(√1.1852737867598 = 1.0887028000147)
1.0887028000147 × (Recall M = 1.4048739495798) = 1.5294902025752
(√1.5294902025752 = 1.2367255971214)
(√1.2367255971214 = 1.1120816503843)
1.1120816503843 × (Recall M = 1.4048739495798) = 1.5623345404306
(√1.5623345404306 = 1.2499338144200)
(√1.2499338144200 = 1.1180043892669)
1.1180043892669 × (Recall M = 1.4048739495798) = 1.5706552419969
(√1.5706552419969 = 1.2532578513606)
(√1.2532578513606 = 1.1194899960967)


세상의모든계산기 님의 최근 댓글
[fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10 엑셀 / 행의 최대 개수, 열의 최대 개수, 셀의 최대 개수 엑셀의 행 개수 제한은 파일 형식에 따라 다르며, 최신 .xlsx 파일 형식은 시트당 최대 1,048,576행까지 지원하지만, 구형 .xls 파일은 65,536행으로 제한됩니다. 따라서 대용량 데이터를 다룰 때는 반드시 최신 파일 형식(.)으로 저장해야 하며, 행과 열의 총 수는 1,048,576행 x 16,384열이 최대입니다. 주요 행 개수 제한 사항: 최신 파일 형식 (.xlsx, .xlsm, .xlsb 등): 시트당 1,048,576행 (2^20). 구형 파일 형식 (.xls): 시트당 65,536행 (2^16). 그 외 알아두면 좋은 점: 최대 행 수: 1,048,576행 (100만여개) 최대 열 수: 16,384열 (XFD) 대용량 데이터 처리: 65,536행을 초과하는 데이터를 다루려면 반드시 .xlsx 형식으로 저장하고 사용해야 합니다. 문제 해결: 데이터가 많아 엑셀이 멈추거나 오류가 발생하면, 불필요한 빈 행을 정리하거나 Inquire 추가 기능을 활용하여 파일을 최적화할 수 있습니다. 2026 02.10