- HP HP Prime
Solve로 삼각함수 해가 안나옵니다
SOLVE(SIN(x)=1)로 하거나 범위를 지정해주더라도 pi/2라는 답이 안나옵니다
댓글12
-
세상의모든계산기
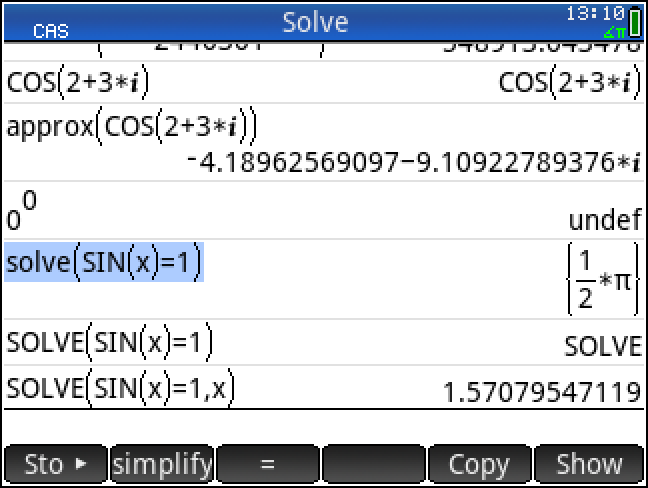
용법이 다르니
solve 와 SOLVE 를 구분해 쓰셔야 합니다.
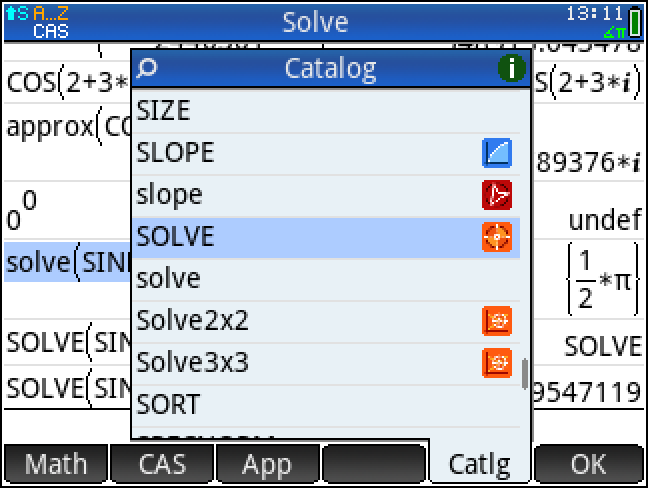
SOLVE 는 App
solve 는 함수 function
-
1
세상의모든계산기
Solve app
The Solve app enables you to define up to ten equations or expressions each with as many variables as you like.
You can solve a single equation or expression for one of its variables, based on a seed value.
You can also solve a system of equations (linear or non-linear), again using seed values.
✦ Solve 앱을 사용하면 원하는 만큼 많은 변수를 포함하는 방정식이나 수식을 최대 10개까지 정의할 수 있습니다.
시드값(seed value)을 기반으로 단일 방정식이나 수식을 특정 변수에 대해 풀 수 있습니다.
또한 시드값을 사용하여 선형 또는 비선형 연립 방정식을 풀 수도 있습니다.
- 1
-
-
1
세상의모든계산기
원래 삼각함수같은 주기함수가 공학용 계산기 solve 와 친하지 않은 것은 널리 알려져 있습니다만...
해에서 접선의 기울기가 0이 되어 나타난 버그에 가까운 것 현상 같습니다.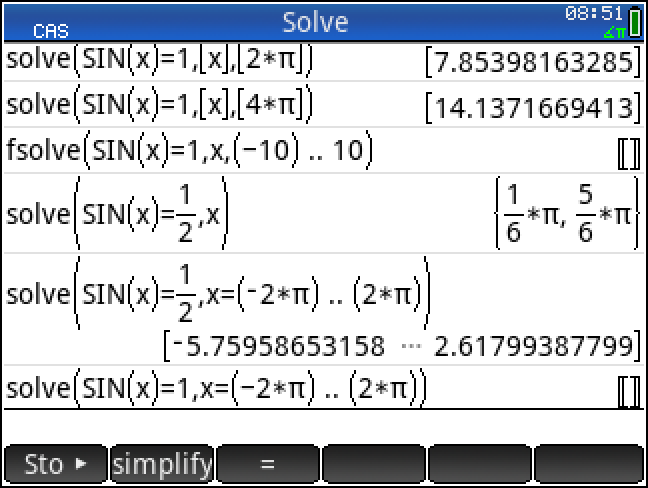
-
세상의모든계산기
Gemini-2.5-pro 답변
✦ HP Prime 계산기의 solve 함수가 sin(x) = 1과 같은 특정 값의 해를 찾지 못하는 문제에 대해 문의하셨군요.
sin(x)=1/2에서는 정상적으로 동작하는데 sin(x)=1에서는 빈 결과([])가 나오는 현상은 해당 계산기 또는 유사한
CAS(Computer Algebra System)에서 나타날 수 있는 동작입니다.이 문제의 원인과 해결 방법을 자세히 설명해 드리겠습니다.
문제의 원인: 수치 해석 알고리즘의 한계
HP Prime의 solve 기능은 내부적으로 수치 해석 알고리즘을 사용하여 해를 찾습니다. 많은 경우, 이 알고리즘은
방정식의 해를 찾기 위해 함수 값의 부호가 바뀌는 지점(sign change)을 탐색합니다.1. `sin(x) = 1/2`의 경우 (정상 작동):
* 이 방정식은 f(x) = sin(x) - 1/2가 0이 되는 x를 찾는 것과 같습니다.
* f(x) 함수의 그래프는 해가 되는 지점에서 x축을 가로지릅니다. 즉, 함수 값이 음수(-)에서 양수(+)로, 또는
양수(+)에서 음수(-)로 부호가 명확하게 바뀝니다.
* solve 알고리즘은 이 부호 변화를 감지하여 해를 성공적으로 찾아냅니다.2. `sin(x) = 1`의 경우 (문제가 발생하는 경우):
* 이 방정식은 f(x) = sin(x) - 1이 0이 되는 x를 찾는 것과 같습니다.
* sin(x)의 최댓값은 1이므로, f(x) 함수는 항상 0보다 작거나 같습니다 (f(x) ≤ 0).
* 따라서 f(x) 그래프는 해가 되는 지점(x = π/2, -3π/2 등)에서 x축에 접할 뿐, 가로지르지 않습니다.
* 결과적으로 함수 값의 부호 변화가 발생하지 않으므로, 부호 변화를 기반으로 해를 찾는 알고리즘은 해가
존재함에도 불구하고 이를 감지하지 못하고 빈 결과를 반환할 수 있습니다.이는 solve 함수의 버그라기보다는, 특정 유형의 문제(함수가 x축에 접하는 경우)에 대한 수치 해석 알고리즘의
본질적인 한계에 가깝습니다.해결 방법
이러한 문제를 우회하여 정확한 해를 찾는 몇 가지 방법이 있습니다.
방법 1: 미분을 이용해 극점 찾기 (가장 안정적인 방법)
sin(x) = 1이 되는 지점은 sin(x) 함수의 극대점(local maximum)입니다. 함수의 극점은 도함수(derivative)가 0이
되는 지점에 존재하므로, 다음 단계를 따를 수 있습니다.1. 도함수가 0이 되는 지점 찾기:
sin(x)의 도함수는 cos(x)입니다. 따라서 먼저 cos(x) = 0의 해를 구합니다.
1 solve(cos(x) = 0, x = ((-2*π) .. (2*π)))
이 명령은 결과로 -3π/2, -π/2, π/2, 3π/2에 해당하는 숫자 값들을 반환할 것입니다.
(예: [-4.712..., -1.570..., 1.570..., 4.712...])2. 후보 값들을 원래 함수에서 확인하기:
위에서 찾은 x 값들을 원래 함수 sin(x)에 대입하여 값이 1이 되는지 확인합니다.
* sin(-3π/2) → 1 (정답)
* sin(-π/2) → -1
* sin(π/2) → 1 (정답)
* sin(3π/2) → -1이 방법을 통해 원하는 구간 내의 모든 정확한 해(-3π/2와 π/2)를 찾을 수 있습니다.
방법 2: 근사값 이용하기
1 대신 1에 아주 약간 작은 값(예: 0.999999999)을 사용하여 방정식을 풀면, 함수가 x축을 미세하게 가로지르게 되어
solve 알고리즘이 해를 찾을 수 있습니다.1 solve(sin(x) = 0.999999999, x = ((-2*π) .. (2*π)))
이 방법은 π/2와 -3π/2에 매우 가까운 근사해를 제공합니다.
방법 3: 그래프 기능 활용
1. 함수 플로터(Function plotter)에서 Y1 = sin(X)와 Y2 = 1을 입력하여 두 함수의 그래프를 그립니다.
2. 그래프 상에서 두 함수가 만나는 점(교점)을 시각적으로 확인하거나, 계산기의 교점 찾기(Intersection) 기능을
사용하여 정확한 x 좌표를 찾습니다.이러한 방법들을 활용하시면 HP Prime 계산기에서 sin(x)=1과 같은 방정식의 해도 성공적으로 구하실 수 있습니다.
-
1
세상의모든계산기
HP Prime 에 적용
방법1)
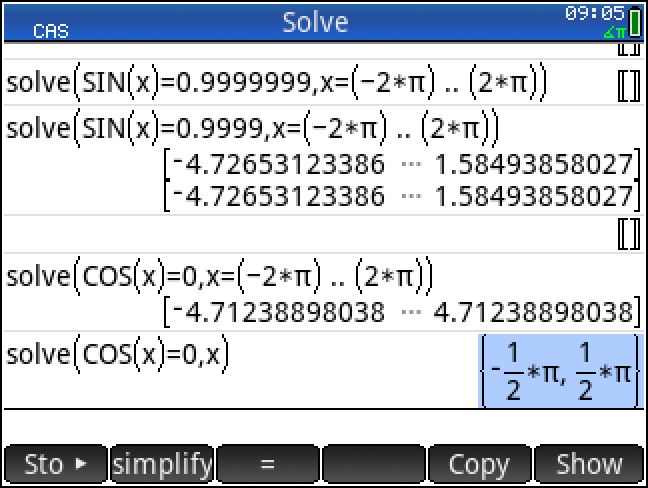
ㄴ 검증 필요해서 번거로움
방법2)
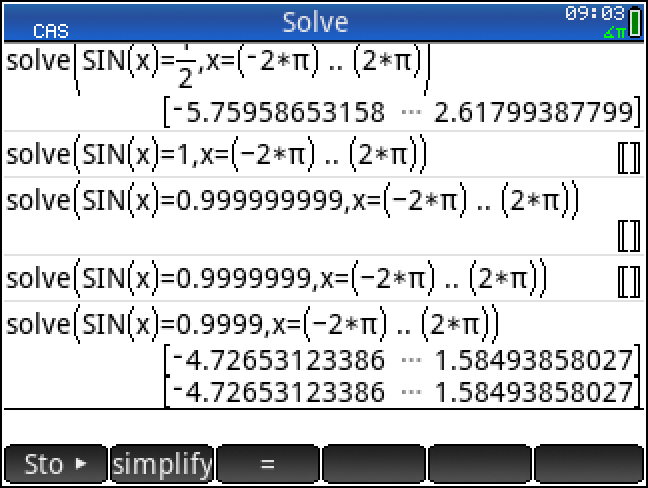
ㄴ 1에 너무 가까우면 안나오고 적당히 떨어져 있어야 하는 듯 함.
ㄴ 오차가 약간 발생함.
방법3)
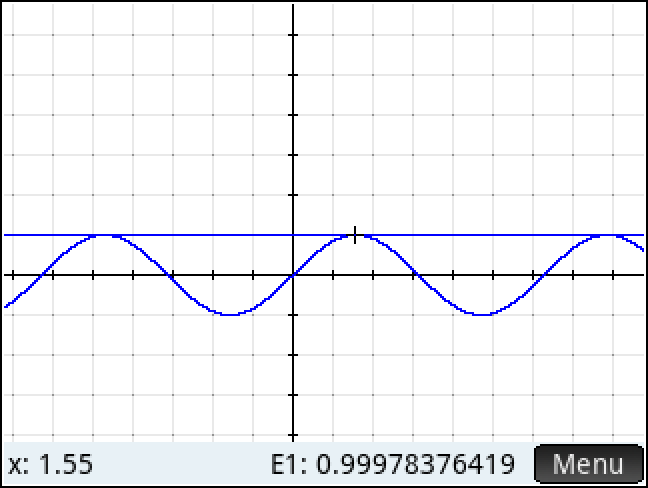
ㄴ TRACE : 정밀하지 않음
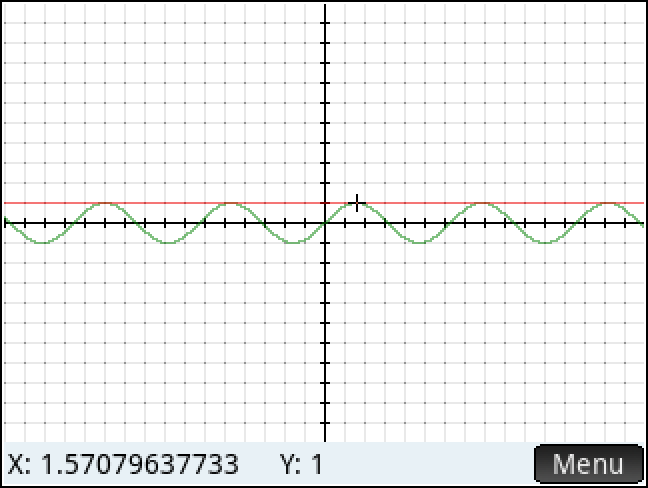
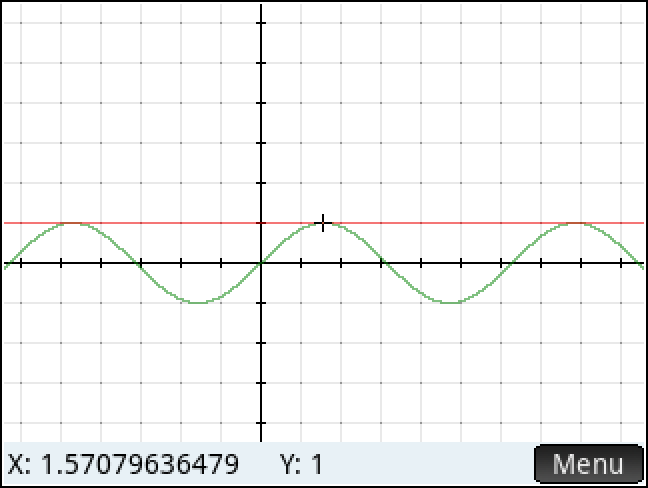
ㄴ Intersection : 약간 시간 걸림 & 오차 발생할 수 있음.
- 1
-
세상의모든계산기
참고

x=guess 는 iterative 방식(일반적으로는 newton's method를 의미함)을
x=xmin .. xmax 는 bisection 방식을 사용하는 듯 합니다. // 구간지정 개념과는 차이가 있는 듯?
-
세상의모든계산기
종합해서 답변을 드리면
HP Prime 에 solve 에서 변수명에 구간을 입력하면
수치해석 방식으로 bisection 을 사용함.
이 bisection 방식은
해의 좌-우 부호가 서로 바뀌어야만 해를 인식하고
해의 좌-우 부호가 같으면 해를 인식하지 못합니다.
이 때문에 본문 sin 의 예나 아래 사진의 예에서는 해를 인식하지 못하는 것으로 보입니다.
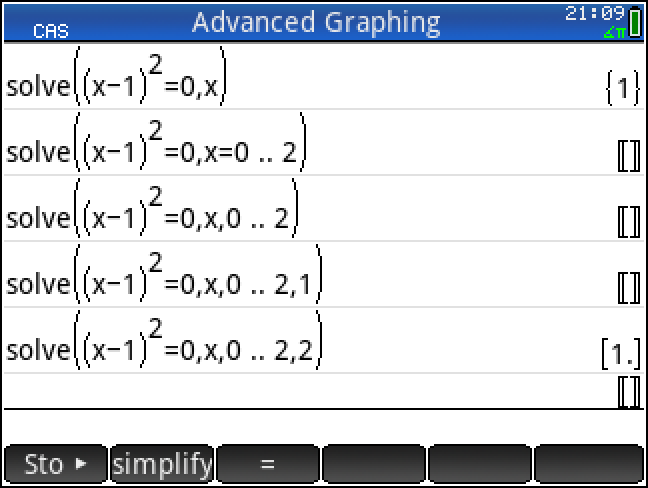
-
1
세상의모든계산기
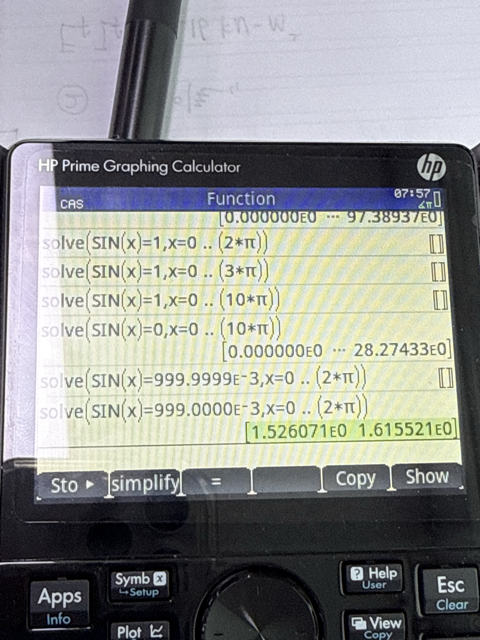
수치해석 방법 method 를 강제로 선택할 수 있으면 좋을텐데...
위의 스샷을 보면 되는 듯 하면서도아래 스샷을 보면 안되는 것 같기도 합니다.
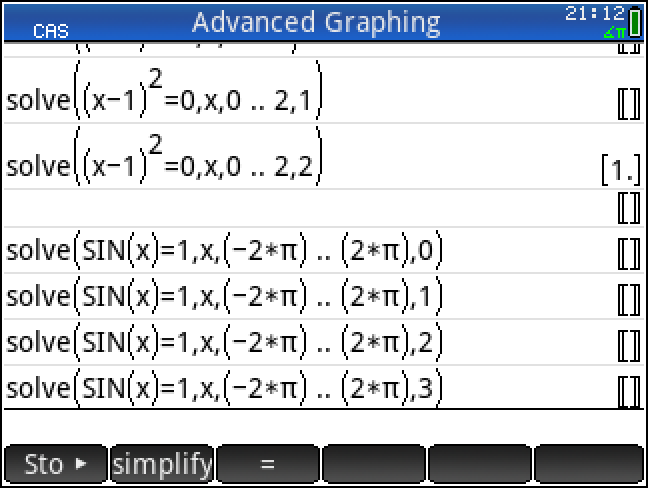
solve(Expr,[Var])
csolve(LstEq,LstVar)
nSolve(Expr,Var,[Guess or Interval],[Method])
deSolve(Eq,[TimeVar],FncVar)
linsolve(LstLinEq,LstVar)
fsolve(Expr,Var,[Guess or Interval],[Method])


KaebbiDo 님의 최근 댓글