- 세상의 모든 계산기 수학, 과학, 공학 이야기 수학 ()
Newton's Method (Iteration 반복법, Newton-Raphson 뉴튼-랩슨법)
http://en.wikipedia.org/wiki/Newton's_method
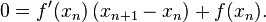
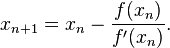
댓글5
-
세상의모든계산기2015.03.23 - 11:24 #6043
Square root of a number[edit]
Consider the problem of finding the square root of a number. Newton's method is one of many methods of computing square roots.
For example, if one wishes to find the square root of 612, this is equivalent to finding the solution to
The function to use in Newton's method is then,
with derivative,
With an initial guess of 10, the sequence given by Newton's method is
where the correct digits are underlined. With only a few iterations one can obtain a solution accurate to many decimal places.
- 1
-
세상의모든계산기
http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=221245100
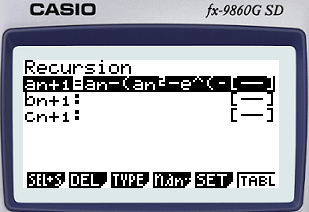
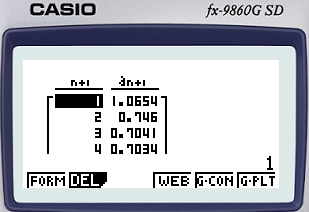
다음 연립방정식의 해를 구하라(단, 해들은 모두 소수점 이하 9째 자리까지 표기)
y=x^2 과 y=e^(-x). 초기값=2

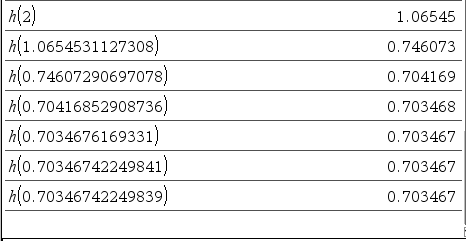
처음에만 h(2) 이후에는 h(ans) ctrl + enter
-
1
-
1


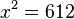
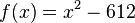

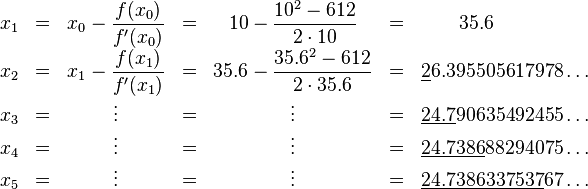
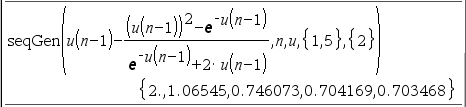
세상의모든계산기 님의 최근 댓글
2번 사진 3개 사진 공통적으로 구석(corner) 에 증상이 있다는 특징이 있네요. 영상 찾아보니 이 가능성이 가장 높은 듯 합니다. https://www.youtube.com/watch?v=zxRBohepzwc ㄴ Liquid Crystal Leakage (액정 누설). ㄴ 손으로 밀어내니 주변으로 밀려나네요. 그래서 점으로 보이기도 하구요. 2025 10.29 500! 의 십진수 근사값 확인 500! = 1.22013682599111006870123878542304692625357434280319284219241358838 × 10^(1134) (참값, 울프람 알파) 2025 10.29 관련 라이브러리 https://allcalc.org/56263 sgn(x) 내장된 부호 함수(signum function)와 달리, 이 함수의 sgn(0)은 0을 반환합니다. 2025 10.29 라이브러리로 사용할 수 있습니다. (제작자 추천) 1. mylib 폴더에 넣기 2. Actions ➡️ library ➡️ refresh libraries 실행 하기 2025 10.29 ChatGPT-5 기호(÷, /, :) 자체는 의미적으로 같은 “나눗셈”을 뜻하지만, 문맥(사람이 쓰는 수학 vs 컴퓨터/프로그래밍)에 따라 해석 우선순위가 달라질 수 있습니다. 🔹 1️⃣ 전통 수학 표기 — ÷, /, : 수학 교과서, 논문, 일반 문서 등에서는 셋 다 의미적으로 “나누기”로 간주됩니다. 즉, 48÷2(9+3), 48/2(9+3), 48:2(9+3) 은 같은 의미로 받아들여야 합니다. 모두 사람의 수학 관행적 해석이 적용되어 48 ÷ 2 × (9+3) = 288 로 처리되죠. 즉, 기호가 바뀌어도 결과는 바뀌지 않습니다. 🔹 2️⃣ 컴퓨터·프로그래밍 문맥에서 / 사용 시 컴퓨터는 “생략된 곱셈(implicit multiplication)”을 따로 구분하지 못합니다. 따라서 다음 두 식은 완전히 다르게 인식됩니다. 표현 파이썬 등에서 해석 결과 48 / 2*(9+3) ((48 / 2) * (9+3)) 288 48 / 2(9+3) ❌ 문법 오류 (생략된 곱셈 인식 불가) — 즉, 컴퓨터 언어에서는 생략된 곱셈이 허용되지 않기 때문에, /는 반드시 명시적 *와 함께 써야 합니다. 🔹 3️⃣ “:” 기호의 경우 현대 수학에서는 “비율”을 나타내는 기호로 쓰입니다. a:b = \frac{a}{b} 따라서 (27 : 3(1+2)3) 같은 표현은 모호하거나 비표준적으로 간주됩니다. 대부분의 경우 계산기로는 입력 자체가 불가능합니다. ✅ 정리 기호 의미 결과 변화 주로 쓰이는 문맥 ÷ 나누기 없음 초중등 수학, 일반 표기 / 나누기 없음 (단, 프로그래밍에서는 생략 곱 불허) 수학/컴퓨터 : 비율 (또는 나누기 의미로 혼용) 보통 계산식에서는 사용 안 함 비, 비율 표기 🔹 결론 48 ÷ 2(9+3), 48/2(9+3), 48:2(9+3) 는 “수학적 의미”로는 동일하게 81로 해석됩니다. 하지만 프로그래밍이나 수식 파서(context) 에서는 /만 유효하고, 생략된 곱은 허용되지 않으며, :는 아예 다른 의미(비율)로 인식됩니다. 2025 10.28