직교 좌표계 vs 극좌표계의 시각적 비교
1. 두 개의 극좌표 함수가 있습니다.
2. 직교좌표계에서 표시.
Rectangular Coordinate = 카르테시안 좌표계 Cartesian coordinate system
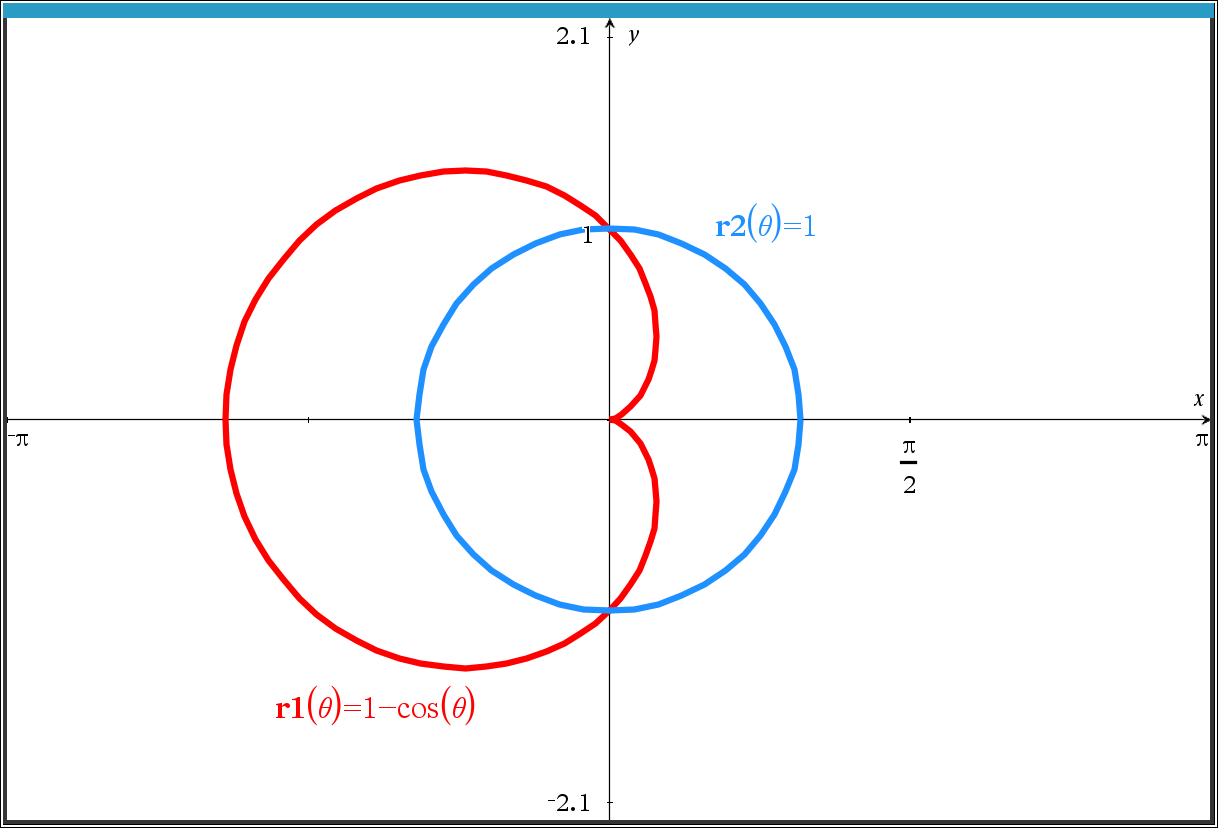
각 축이 서로 수직(직각)으로 만남.
각 축의 값이 커지거나 작아지는 것은 일직선 위에서 발생
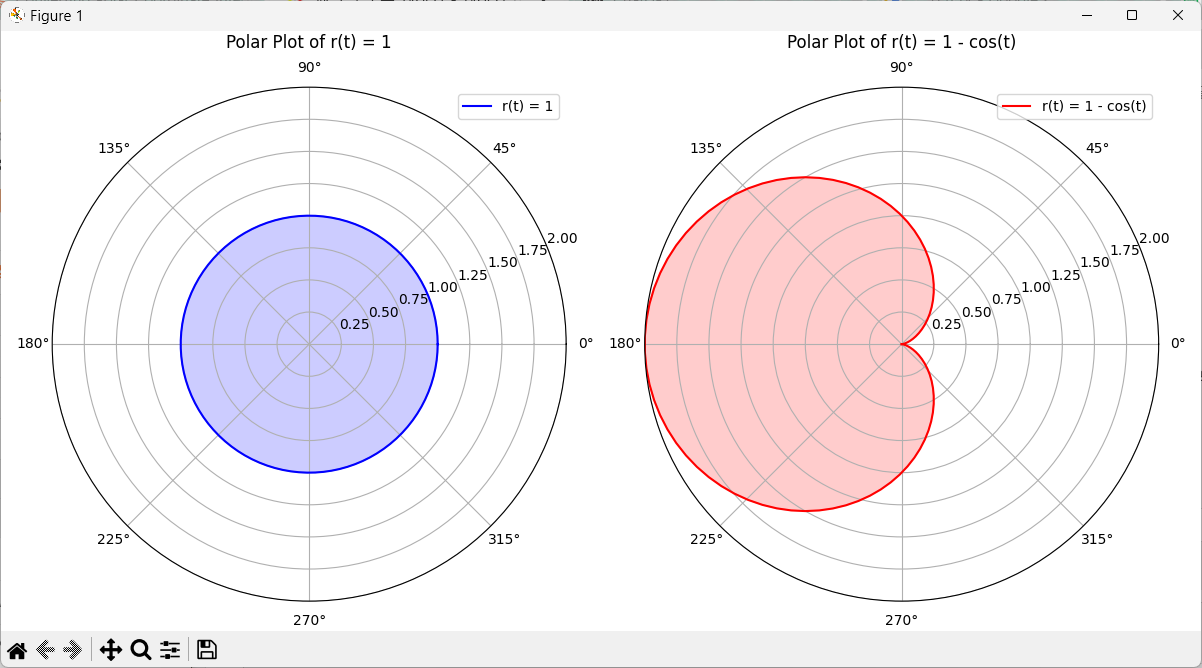
3. 극좌표계에서 표시
Polar Coordinate
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | import numpy as npimport matplotlib.pyplot as plt# t의 범위 설정 (0부터 2π까지)t = np.linspace(0, 2 * np.pi, 100)# 극좌표 함수 정의r1 = np.ones_like(t) # r(t) = 1r2 = 1 - np.cos(t) # r(t) = 1 - cos(t)# 극좌표 그래프 그리기fig = plt.figure(figsize=(12, 6))# r(t) = 1 그래프ax1 = fig.add_subplot(121, projection='polar')ax1.plot(t, r1, label='r(t) = 1', color='b')ax1.fill(t, r1, color='blue', alpha=0.2) # 그래프 아래 영역 채우기ax1.set_title('Polar Plot of r(t) = 1', va='bottom')ax1.set_ylim(0, 2) # 반지름 범위 설정ax1.legend()# r(t) = 1 - cos(t) 그래프ax2 = fig.add_subplot(122, projection='polar')ax2.plot(t, r2, label='r(t) = 1 - cos(t)', color='r')ax2.fill(t, r2, color='red', alpha=0.2) # 그래프 아래 영역 채우기ax2.set_title('Polar Plot of r(t) = 1 - cos(t)', va='bottom')ax2.set_ylim(0, 2) # 반지름 범위 설정ax2.legend()# 그래프 보여주기plt.tight_layout()plt.show() |
극좌표계의 구조
-
각도 축: 극좌표계에서tt 축(각도 축)은 원점을 기준으로 하는 방향을 나타냅니다. 각도는 일반적으로 반시계 방향으로 측정되며, 0에서 2π까지 변화합니다.
-
반지름 축: r 축(반지름)은 원점으로부터의 거리로, 특정 각도에 따라 뻗어 있습니다. 반지름은 원점에서 시작하여 외부로 나아가며, 주어진 각도 t에서의 반지름 r 값에 따라 점이 위치하게 됩니다.
-
동심원: 극좌표계는 다양한 반지름에 대해 중심이 같은 원을 그리는 "동심원" 형태로 되어 있습니다. 즉, 반지름 r의 값에 따라 같은 각도 t에서 원의 크기가 결정됩니다.
4. 비교
- 직교좌표계에서는 x축과 y축이 수직으로 만나며, 각 축이 서로의 기준을 이루는 데 반해,
- 극좌표계에서는 각도와 반지름이 서로 독립적인 성질을 가지며, 각도는 방향을, 반지름은 거리를 나타내게 됩니다.
댓글 4
-
-
-
극좌표계에서의 면적 요소
1. 부채꼴 형상:
- 극좌표계에서2. 사각형 근사:
- 부채꼴의 끝부분이 작아질 때, 이를 사각형으로 근사할 수 있습니다. 이때 사각형의 한 변은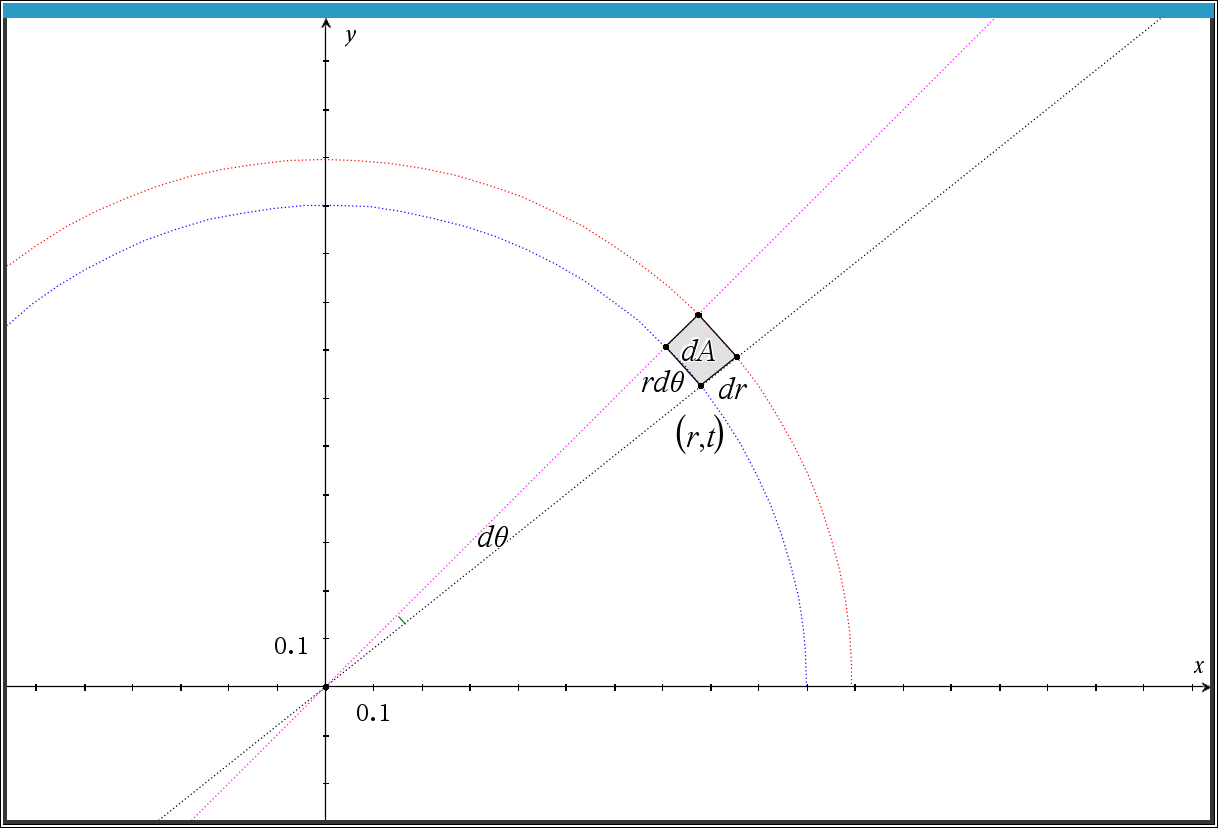
3. 면적 계산:
- 따라서 미소 면적 요소는 다음과 같이 표현할 수 있습니다:
- 여기서
- 즉, 사각형의 면적은 다음과 같이 계산할 수 있습니다:
4. 순서 변경:
- 이 면적 요소는
-
-
-
극좌표 함수의 형태로 나타나는 이중적분
극좌표 함수에서
이 계산식에서
이중적분의 의미
1. 미소 면적의 총합:
- 극좌표계에서
- 즉,2. 변화에 따른 적분:
-결론
결국, 극좌표에서의 이중적분은 각 점의 미소 면적
이때
따라서
-
-
-
이중적분
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273importnumpy as npimportmatplotlib.pyplot as pltfrommatplotlib.animationimportFuncAnimation# 설정t_values=np.linspace(0,2*np.pi,100)# t의 변화 범위# 그래프 초기화fig, ax=plt.subplots(figsize=(8,8))ax.set_xlim(-1.5,1.5)ax.set_ylim(-1.5,1.5)ax.set_aspect('equal')ax.set_title('Area under the curve for varying $t$')ax.set_xlabel('$x$')ax.set_ylabel('$y$')# 그래프에 사용할 점과 면적 표시line_r,=ax.plot([], [], color='blue', label='$r(t) = \sin(t)$')ax.legend()# 면적 다각형 리스트area_patches=[]total_area=0# 총 면적 초기화area_text=ax.text(-1.4,1.2, f'Total Area: {total_area:.2f}', fontsize=12)# 애니메이션 업데이트 함수defupdate(frame):globaltotal_area# 총 면적을 전역 변수로 설정t=t_values[frame]r=np.linspace(0, np.sin(t),100)# r 값 생성x=r*np.cos(t)# x 좌표y=r*np.sin(t)# y 좌표# 면적을 나타내는 다각형 생성area_patch=plt.Polygon(np.column_stack((x, y)), closed=True, color='lightblue', alpha=0.5)ax.add_patch(area_patch)# 다각형 추가area_patches.append(area_patch)# 면적 목록에 추가# 면적 계산 (부채꼴 면적 계산)segment_area=0.5*(np.sin(t)**2)*t# t에 따른 면적total_area+=segment_area# 총 면적 업데이트# 선 업데이트line_r.set_data(np.array([0, x[-1]]), np.array([0, y[-1]]))# 면적 합계 텍스트 업데이트area_text.set_text(f'Total Area: {total_area:.2f}')returnarea_patches, line_r, area_text# 애니메이션 생성ani=FuncAnimation(fig, update, frames=len(t_values), blit=False, repeat=False)# 진행 표시줄 추가progress_ax=fig.add_axes([0.15,0.1,0.7,0.05])# 위치 조정progress_bar=plt.barh([0], [0], color='gray', height=0.1)# 진행 표시줄progress_ax.set_xlim(0,len(t_values))progress_ax.set_ylim(-0.5,0.5)progress_ax.axis('off')# 축 숨기기# 진행 표시줄 레이블 추가start_label=progress_ax.text(-1,0,'Start: $t=0$', fontsize=10, ha='center')end_label=progress_ax.text(len(t_values)+1,0,'End: $t=2\pi$', fontsize=10, ha='center')# 애니메이션 프레임 업데이트defupdate_progress(frame):progress_bar[0].set_width(frame)# 진행 표시줄 업데이트returnprogress_bar# 진행 표시줄 애니메이션ani_progress=FuncAnimation(fig, update_progress, frames=len(t_values), blit=False, repeat=False)plt.show()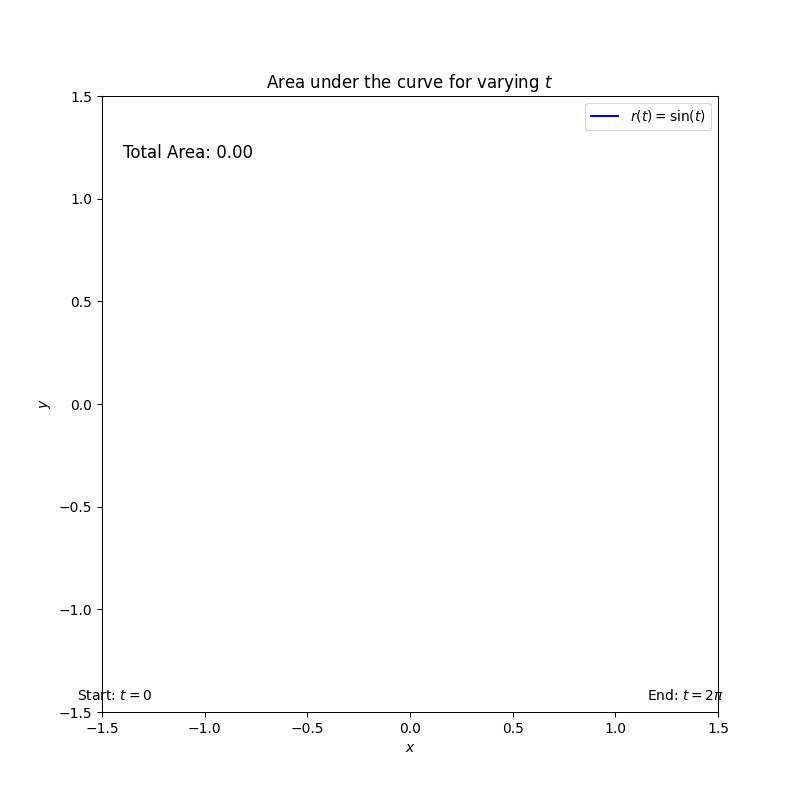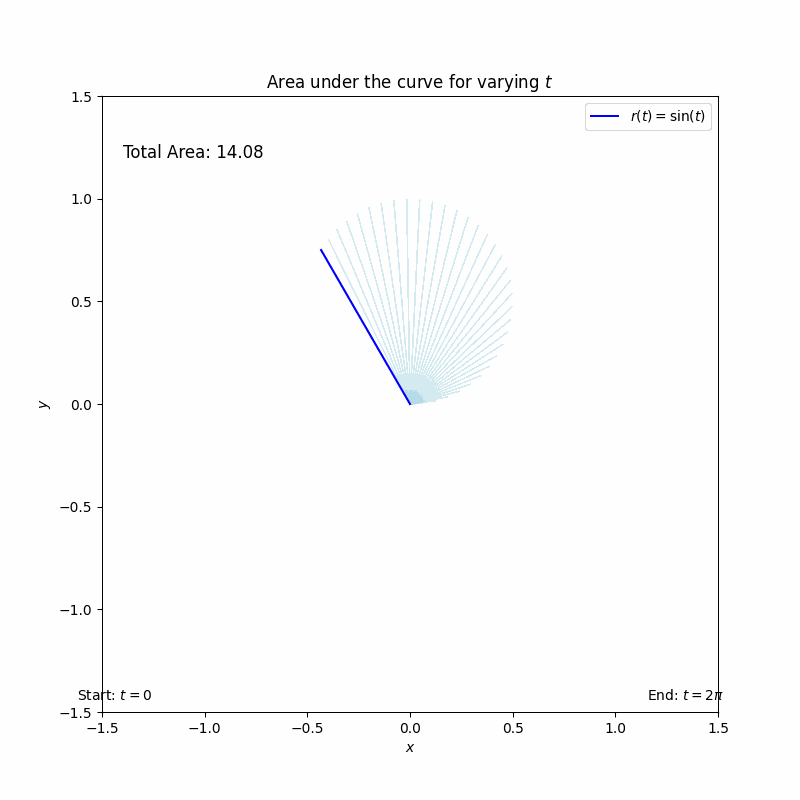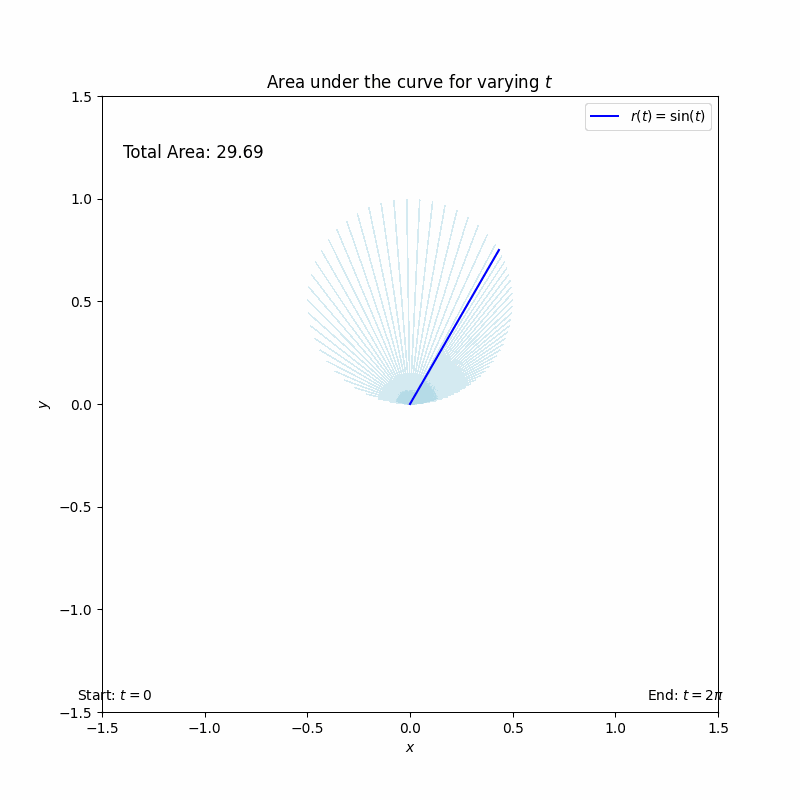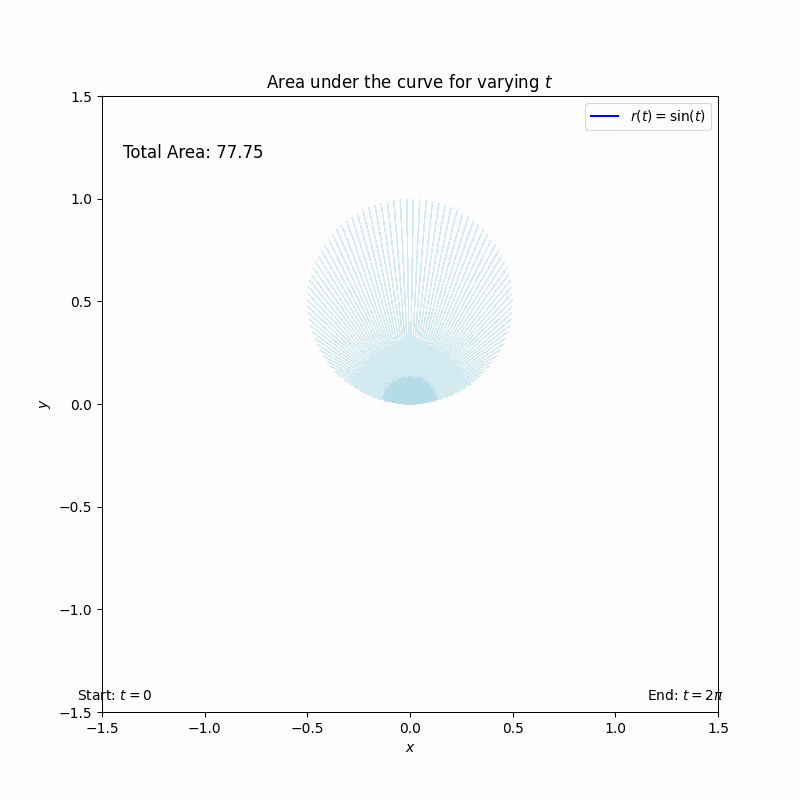
-


참고 : BallPen.blog, 내 나이의 빛깔 - 극좌표계
https://ballpen.blog/%EA%B7%B9%EC%A2%8C%ED%91%9C%EA%B3%84-polar-coordinate-system/