- CASIO 공통
[fx-350], [fx-570] [fx-5800p] [fx-9860G] 설정 - 자릿수 표기 및 반올림 Display Digits 및 Internal Rounding
1. (화면상) 자릿수의 표시 방법 설정
a. [fx-350, 570]의 [MS] 시리즈
아래 화면이 표시될 때까지 【MODE】 버튼을 반복

 【1】 Fix, 【2】 Sci, 【3】 Norm(1~2) 중 하나 선택.
【1】 Fix, 【2】 Sci, 【3】 Norm(1~2) 중 하나 선택.
* 설정에 따른 효과는 [ES] 기종과 동일하므로 아래 설명 참고
* 초기 Default 값은 Norm1
소숫점 표시된 상황에서 【ENG】버튼을 누르면 공학적 표기로 변경되며,
3의 배수 조건에 맞을 경우 일시적으로 과학적 표기로 보이기도 합니다.
 【ENG】
【ENG】
b. [fx-350, 570]의 [ES] 시리즈 및 [fx-5800p]
- 표시 자릿수의 지정 방법
고정 소숫점(FIX) : 【SHIFT】【MODE】【6】【선택 0~9】
유효 자릿수(SCI, 과학적 표기법) : 【SHIFT】【MODE】【7】【선택 0~9】
지수 표시 범위(Norm) : 【SHIFT】【MODE】【8】【선택 1~2】 - 결과의 표시 예
ㄴ 잘 모르겠으면 Norm2 로 【SHIFT】【MODE】【8】【2】 설정하시면 됩니다.FIX 지정된 소숫점 자릿수까지만 표시.
그 아래에서 반올림.
소숫점 이하 큰 자릿수 확인에 부적합100÷7
≒ 14.286 (FIX3)
≒ 14.29 (FIX2)SCI 지정한 유효 자릿수만큼을 항상 표시.
그 아랫에서 반올림.
자릿수가 매우 크거나 매우 작은때 적합1÷7
≒1.4286×₁₀⁻¹ (SCI5)
≒1.429×₁₀⁻¹ (SCI4)Norm 아래의 범위에서는
지수형식으로 표시.
Norm1 : 10⁻²>|x|, |x|≥10¹⁰
Norm2 : 10⁻⁹>|x|, |x|≥10¹⁰1÷200
=5×₁₀⁻³(Norm1)
=0.005 (Norm2)1÷2000000000
=5×₁₀⁻¹⁰
(Norm1, Norm2)
c. [fx-9860G] 시리즈
- 자릿수 표시 형식은 위의 [fx-570]과 같습니다. Norm / Fix / Sci
- 소수점 이하 설정, 유효 단위수 설정을 해도 내부 연산은 기수부 15단위를, 표시 수치는 10단위를 기억하고 있습니다. 이 수치를 설정한 단위수와 일치시키고 싶은 때는 수치 계산 메뉴(NUM)의 내장 함수인 Rnd를 활용하세요.
- 직접 변경하거나 표시 범위 설정(Norm)을 이용하여 변경하기 전까지 소수점 이하 설정(Fix)과 유효단위수 설정(Sci)은 유지됩니다.
조건 조작 표시 【1】【0】【0】【÷】【6】【EXE】 16.66666667 고정 소숫점 4자리
Fix【SHIFT】【MENU】【▲】【▲】【F1】【4】【EXE】【EXIT】【EXE】 16.6667 유효 자릿수 5자리
Sci【SHIFT】【MENU】【▲】【▲】【F2】【5】【EXE】【EXIT】【EXE】 1.6667E+01 설정해제
Norm1 or Norm2【SHIFT】【MENU】【▲】【▲】【F3】【EXIT】【EXE】 16.66666667
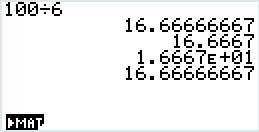
d. [fx-350, 570, 991]의 [EX] 시리즈
- 표시 자릿수의 지정 방법
고정 소숫점(FIX) : 【SHIFT】【MODE】【3】【1】【선택 0~9】
유효 자릿수(SCI, 과학적 표기법) : 【SHIFT】【MODE】【3】【2】【선택 0~9】
지수 표시 범위(Norm) : 【SHIFT】【MODE】【3】【3】【선택 1~2】
* 계산식 입력 후 = 대신 SHIFT = 을 누르면(≒) 계산 결과를 소수점 표시로 나타냅니다.
※ 출처 : 각 계산기 매뉴얼 (참고)
2. 값의 반올림 Internal Rounding : (메모리에) 실제적 효과
1.에서 살펴본 자릿수 표기의 설정은 "실제 결과값(=계산기 내부 유효숫자)을 어떻게 화면에 보여줄 것인가?"를 결정하는 것일 뿐, 실제 결과값(=유효 자릿수)에 영향을 주지 않습니다.
실제의 결과값(=내부 유효숫자)를 화면상 표시된 것과 동일하게 반올림 처리하려면 아래와 같은 별도의 명령(Rnd)을 내려야만 합니다.
[fx-350] [fx-570] [fx-5800]
【SHIFT】【0】

 전 후
전 후

MS 기종에서는 Internal Rounding 명령 전/후 차이를 화면상에서 느낄 수 없음.
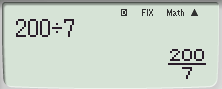
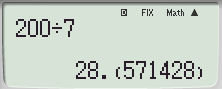
 전
전
후
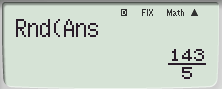
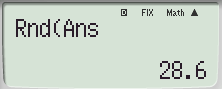
ES 기종에서는 Rnd() 명령을 한 번 더 거쳐야 하므로 그 차이를 바로 알 수가 있습니다.
* fx-570 ES PLUS 기종은 스샷처럼 순환마디 표현이 불가능합니다.
[fx-9860G]
예) 200÷7×14 = 400
| 조건 | 조작 | 표시 |
|---|---|---|
| 【200】【÷】【7】【×】【14】【EXE】 | 400 | |
| 소수점 3단위 설정 |
【SHIFT】【MENU】【▲】【▲】 |
400.000 |
|
소수점 설정과 무관하게 |
【200】【÷】【7】【EXE】 【×】【14】【EXE】 |
28.571 400.000 |
| 화면 표시대로 미표시부분 반올림 (미표시부분 제거) |
【200】【÷】【7】【EXE】 【OPTN】【F6】【F4】【F4】【EXE】
【×】【14】【EXE】 |
28.571 Rnd 28.571 399.994 |
|
소숫점 강제 지정 (반올림) |
【200】【÷】【7】【EXE】 【F6】【F1】【SHIFT】【(-)】【,】【2】【)】【EXE】
【×】【14】【EXE】 |
28.571 RndFix(Ans,2) 28.570 399.980 |
※ 위 계산 결과는 처음부터 순서대로 입력하는 것을 가정합니다.
예를 들어 마지막 RndFix 명령어만 따로 입력하려면 【F6】 앞에 【OPTN】【F6】【F4】를 추가로 입력해야 합니다.
댓글11
-
세상의모든계산기
[fx-9860 G] Norm 설정 방법



 을 눌르고
을 눌르고

Display - Norm 을 선택하여 Norm1 혹은 Norm2 로 쓰시면 됩니다. -
세상의모든계산기
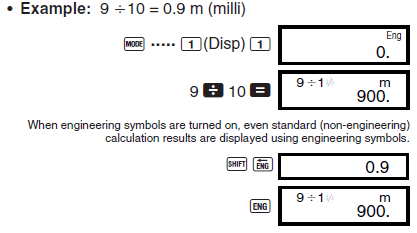
[fx-570MS] ENG 모드 (과학적 함수 계산시)
예를 들어 5÷10 을 하면 일반 표시모드에서는 0.5가 나오지만, 이것을 500 m 로 나오도록 설정할 수 있습니다.
사용자설명서의 과학적 함수 계산 파트를 참조하세요. (영문 설명서 Inputting Engineering Symbols)
참고글
 http://www.allcalc.org/10393
http://www.allcalc.org/10393 -
1
세상의모든계산기
[ES][EX] 기종은 SI Metric 으로 표시되진 않습니다.
MS와 같은 기능이 있긴 하지만 SI Metric 이 붙진 않고,
 버튼을 누르면 3의 배수로
버튼을 누르면 3의 배수로  을 이용한 표기가 이어집니다.
을 이용한 표기가 이어집니다. 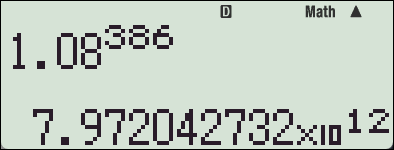 T
T  G
G 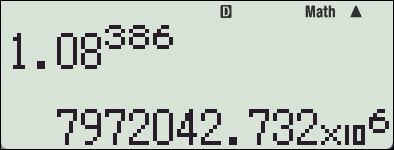 M
M 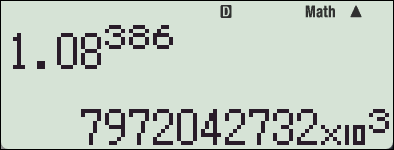 k
k -
1
세상의모든계산기
1. 일단 순환 소수(recurring decimal) 표시를 지원하는 계산기에서만 설정이 가능합니다.

└ fx-115ES PLUS _ fx-991ES PLUS C 사용자 설명서 중 발췌 (SETUP 메뉴 중 있음)
본문 스샷에 사용된 계산기는 제 기억으로 fx-570VN PLUS 입니다. (예전에 썼던거라 기억이 가물가물)2. fx-570ES Plus, fx-570ES Plus 2nd Edition 등
국내 유통중인 대부분의 계산기는 순환 소수 표시를 지원하지 않습니다.
3. 질문하실 때는 항상 질문하려는 계산기 모델명을 정확하게 적으셔야 합니다.
-
1
세상의모든계산기

어떻게 해야 하는가가 문제가 아니고, 각각의 설정이 표시하려는 내용(목표?)를 이해 하시는게 먼저일 듯 합니다.
그리고, 질문하신 내용만 보고서는
원하시는게 뭔지도 모르겠고,
계산기를 가지고 정확하게 무슨 조작을 하셨는지도 모르겠습니다. -
-
세상의모든계산기
질문 : 2.5x10^-3 ⇒ 25x10^-4 로 바뀌어 나오게 못하나요?
불가능합니다.
곱하기 앞의 숫자는 정수부가 1자리만 남도록 기본적으로 설계되어 있습니다.
예외로
【ENG】버튼을 눌러 지수부가 3의 배수가 되도록 변경할 수만 있을 뿐입니다.

【S⇔D】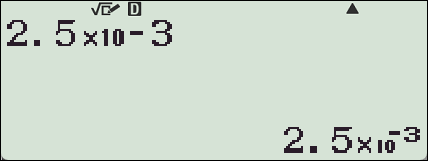
【ENG】
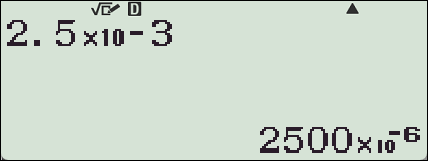
【ENG】
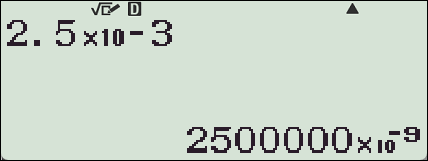
【ENG】
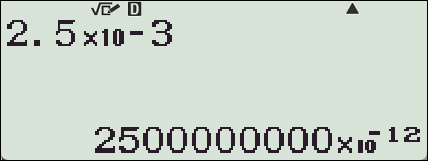



세상의모든계산기 님의 최근 댓글
감사합니다. 주말 잘 보내세요. 2026 03.06 [fx-570 ES] 과학 상수를 이용한 계산에서 에러 발생 상황 https://kin.naver.com/qna/detail.naver?d1id=11&dirId=1118&docId=492235162&page=1&answerNo=1 vs 2026 03.01 과학상수를 이용한 계산 중 자릿수 한계로 인한 에러 발생 가능성 https://allcalc.org:443/board_calculators/6925#comment_57029 2026 03.01 기본 어댑터 MODEL : AD0301-1202500GB INPUT : 100~240V, 50~60Hz, 0.8A Max OUTPUT : 12.0V, 2.5A, 30.0W ㄴ 측정시 플러그 외경/내경 : 5.5mm / 2mm 2026 02.15 엑셀 파일로 만드니 전체 160~200MB 정도 나옵니다. 읽고 / 저장하는데 한참 걸리네요. 컴 사양을 좀 탈 것 같습니다. -> 엑셀/한셀에서 읽히지만, 구글 스프레드시트에서는 열리지 않네요. 100만 개 단위로 끊어서 20MB 정도로 분할해 저장하는 편이 오히려 속 편할 것 같습니다. -> 이건 구글 스프레드시트에서도 열리긴 하네요. (약간 버퍼링?이 있습니다) 2026 02.10